Je vous propose un défi amusant qui va nous plonger au coeur de la relativité et des lois de l'induction.
Dans un premier temps rappelons une expérience de pensée citée par Feynmann dans son fameux cours :
Soit une fil horizontal parcourue par un courant continu d'intensité I.
Pour simplifier le problème nous considérons que tous les électrons sont en mouvement et se déplacent à vitesse u.
Soit rho_e = la densité de charge négative due aux électrons et rho_p la densité de charge positive due aux protons.
La densité totale de charge vaut bien sûr rho = rho_p + rho_e = 0.
Le courant I s'exprime par I = rho_e * u * S = j * S.
où j=(jx,jy,jz) est le vecteur densité de courant. La relativité restreinte nous enseigne que (jx,jy,jz,rho) forme un quadrivecteur, c'est à dire que ses composantes (jx',jy',jz',rho') se transforment en utilisant les transfos de Lorentz de la même manière que (x,y,z,t).
Nous voulons savoir quelle est la densité de charge totale rho' et de courant j' perçues par un observateur dans un référentiel R' animé d'une vitesse v parallèle par rapport au fil (référentiel R).
Appliquons donc les TL, initialement dans R on a (jx=j0, jy=0, jz=0, rho=0)
avec j0 = rho_e * u
dans R' :
jx' = gamma.j0 = gamma * rho_e * u,
jy' = 0
jz' = 0
rho' = -gamma * rho_e * u * v / c^2
avec gamma = 1/(1 - (v/c)^2)^0.5
En ne considérant que la contraction des longueurs nous pouvons facilement vérifier ce résultat en supposant que l'observateur se déplace à la même vitesse que les électrons (v = u).
Dans R', les électrons sont au repos, l'espacement entre 2 électrons s'est dilaté d'un facteur gamma. La densité rho_e' vaut donc rho_e/gamma.
Les protons sont par contre vus en mouvement, leur densité de charge est multipliée par gamma de sorte que rho_p' = gamma * rho_p = - gamma * rho_e.
Nous avons donc rho' = rho_e * (1/gamma - gamma) et on retrouve bien rho' = -gamma * rho_e * v^2/c^2.
L'interprétation de ce résultat c'est que l'observateur qui se déplace parallèlement à une ligne de courant voit apparaitre une densité de charge dans le fil et subit donc une force dirigée vers le fil, pour lui cette force est une interaction Coulombienne .
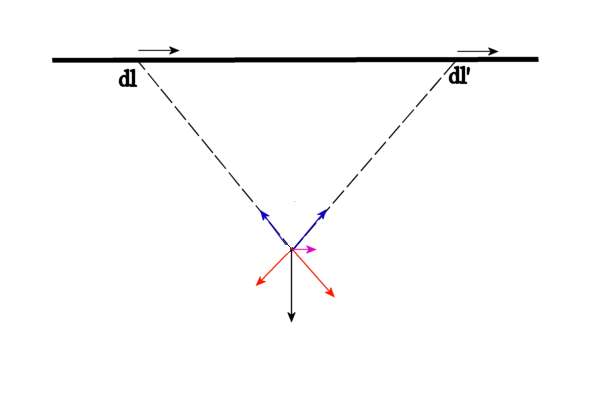
Maintenant, l'exercice que je demande est beaucoup plus compliqué, l'observateur ne se déplace plus parallèlement au fil mais perpendiculairement, il se dirige donc vers le fil. Le résultat est connu, si on regarde les lignes de champ magnétique dans le référentiel de R on voit immédiatement que la force de Lorentz est dirigée parallèlement au .
Si on essaye d'interpréter ce résultat en suivant un raisonnement similaire au cas précédent, nous sommes frappés de constater que l'observateur subit une force dans une direction parallèle au fil, donc orientée dans une région de l'espace où il n'y a pas de charges (sic)!
Le raisonnement précédent ne peut donc plus s'appliquer, l'interaction ressentie ne peut plus être Coulombienne.
L'exercice que je propose est donc de trouver une interprétation similaire à celle de Feynmann pour expliquer ce qui se passe dans le cas où la vitesse de l'observateur est perpendiculaire au fil.
PS : Problème déjà proposé sur fr.sci.physique, le problème posé n'est pas une simple question mais un véritable défi de vulgarisation lancé aux contributeurs de futura.
-----




 .
.