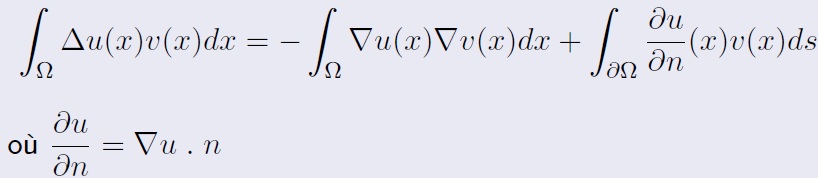salut tous,
j'aimerai savoir comment on fait les intégrations par parties que j'appel "généralisées" (je ne sais pas si le terme est correct)..
je voudrais intégrer par partie ceci :
et ceci:
et je ne sais pas trop comment faire ni pour la divergence ni pour le gradient...
et le fait que ça soit une intégrale triple me bloquee aussi...;
je vous remercie d'avance pour votre aide
pas d'idée ... ? peut etre que les physiciens du forums auront plus l'habitude de manier ces choses ....
Déplacé vers Physique.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
je viens de trouver un document intéressant mais je ne sais pas trop comment appliquer ceci sur les cas que j'ai cité plus haut et je n'ai pas vraiment compris la demonstration de cette relation:
pourriez vous m'aider svp ?
merci
Bonsoir,
Je te conseille vivement de te pencher sur la notation indicielle pour le calcul tensoriel. Tu verras alors qu'avec ce formalisme tout fonctionne de manière très semblable à ce que tu connais déjà et que le fait d'être en dimension supérieure à 1 n'importe que peu dans les calculs.
Regarde par exemple ce document, en particulier vers la page 16.
super, merci beaucoup pour ce document ça répond éxactement à ma question !
=> par contre ça m'intéresserai de connaitre la démonstration de cette formule si quelqu'un la connait...
Le cadre mathématique le plus adapté est celui de l'intégration des formes différentielles dans lequel se place la version moderne du théorème de Stokes. Dans ce cadre, ce n'est quasiment rien de plus que l'application de la règle de Leibniz.
merci beaucoup !!!
