Bonjour,
Je suis élève en école d'ingénieur électronique et je dois réaliser pour un projet la modélisation informatique d'un système mettant en oeuvre un électroaimant.
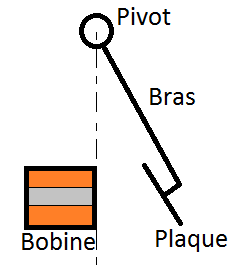
Voici ci dessous la représentation de mon problème :
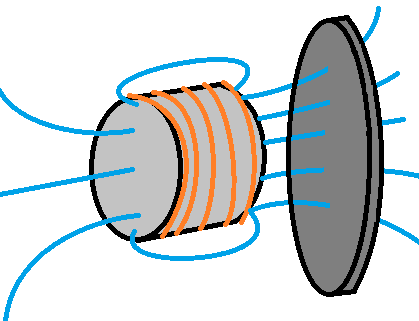
Le matériau ferromagnétique est en fait entouré de plusieurs couches de spires. A droite, la plaque à attirer. Voici mon(mes) problème(s) :
D'une part j'ai utilisé des hypothèses me permettant de calculer l'inductance de ma self. Je tiens bien compte de la non linéarité de la perméabilité du noyau, mais la géométrie de la bobine (longueur équivalente à la largeur) ne me permet pas à mon avis d'utiliser la formule :
L=(mu_0xmu_r*N*S)/lg
mu_0 : perméabilité du vide
mu_r : // // matériau
N : Nombre de spires
S : surface du noyau
lg : longueur du noyau
Ensuite, je pense que le concept de champ magnétique pour moi n'est pas très clair. Je fais le calcul H=NxI/lg et j en déduis B=mu_0 x mu_r x H
Pour moi ce B calculé est la valeur du champ sur la ligne central traversant le noyau.
Ensuite qqchose n'est pas clair : j'ai lu a plusieurs reprise que comme le circuit magnétique n'est pas fermé, je ne peux calculer le flux Phi = BxS au sein du matériaux....ce concept m'échappe...
Ensuite (oui il y a bcp de choses pas claires) : je cherche une méthode pour calculer la force que pourra exercer mon electroaimant sur a plaque circulaire située à droite sur mon dessin.
J'ai vu la formule de picou etc mais j avoue que je n'étais pas tout a fait convaincu.
En somme je chercherais une méthode permettant de simplifier mon modèle afin de calculer les différentes caractéristiques de mon système : le paramètre final à déterminer étant la force qu'exercera l'electroaimant sur la plaque.
Le but est aussi de modéliser mon système sur ordi en rentrant les équations du problème, en pouvant paramétrer différentes choses : nbres de spires, dimension de la bobine, du noyau, distance initiale de la plaque a attirer etc... quelqu un pourrait me guider et éclaircir certains points qui me sont assez obscure ?
Je vous remercie par avance de l'attention que vous porterez à mon problème.
Bien cordialement,
coco86
-----




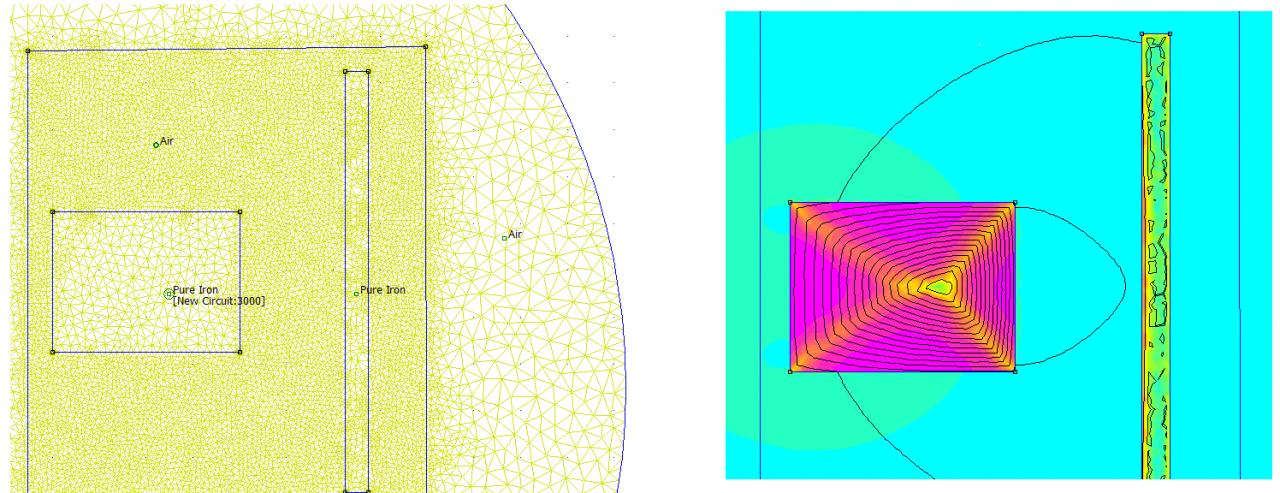

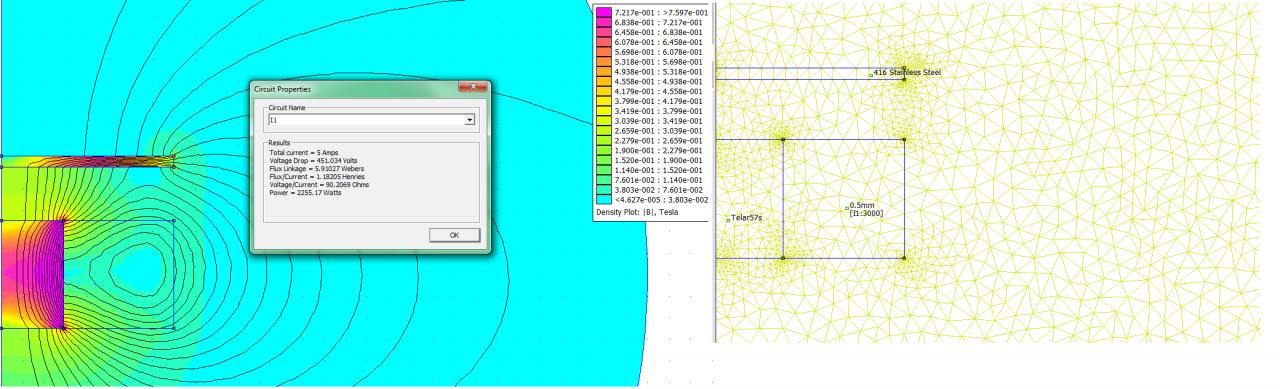
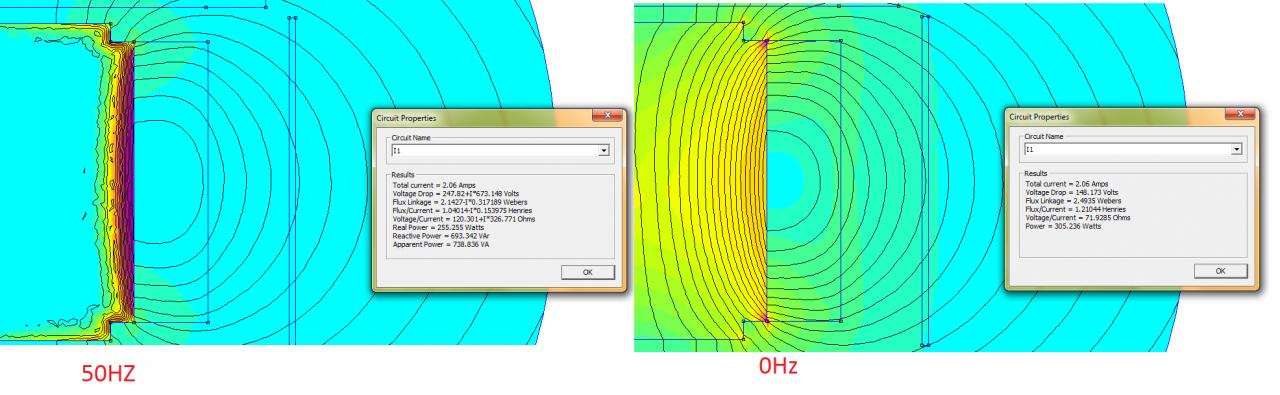
 . L'axe de symétrie est le bon, les lignes de flux font comme si elles se bouclaient à l'extérieur de ta frontière (c'est donc que les conditions aux limites sont les bonnes), les valeurs de quelques dixièmes de tesla me plaisent bien. Tu as vraiment 3000 tours sur ta bobine ? N'hésite pas à mailler un peu plus fin, avoir un seul élément dans l'épaisseur de la plaque, c'est trop juste.
. L'axe de symétrie est le bon, les lignes de flux font comme si elles se bouclaient à l'extérieur de ta frontière (c'est donc que les conditions aux limites sont les bonnes), les valeurs de quelques dixièmes de tesla me plaisent bien. Tu as vraiment 3000 tours sur ta bobine ? N'hésite pas à mailler un peu plus fin, avoir un seul élément dans l'épaisseur de la plaque, c'est trop juste.