Mécanique de Newton

[invite67e9590d]

Bonjour,

Je révises pour le bac et j'enchaîne les annales... Malheureusement ce n'est pas toujours expliqué en détails !

Voilà l'énoncé:

" Un lugeur se lance sur une piste avec une vitesse initiale de 2,0 m/s à l'instant t=0. La piste est plane et rectiligne, elle est inclinée par rapport à l'horizontale d'un angle de valeur x = 12° . La masse de la luge et de son lugeur est : m= 62kg. On donne la valeur de la pesanteur: g= 9,8 m/s² .

On néglige tout frottement pendant le mouvement.

Déterminez l'accélération du système.

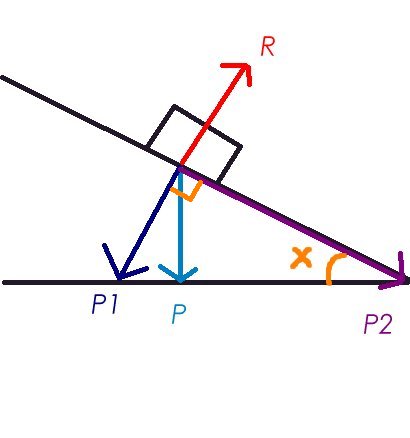
J'ai fait l'inventaire des forces, soit : le poids (vecteur)P et la réaction du support (vecteur)R.
J'en déduis, d'après la deuxième loi de Newton: (vecteur)P+(vecteur)R = m.(vecteur)a

Je ne comprends pas comment obtenir la valeur de R.
Sachant que la solution est mg.sin(x) + 0 = ma ...
Ca voudrait dire que R=0 ?
-----

[LPFR]

Bonjour.
Faites un dessin.
R est la réaction du sol. Elle est égale à la composante du poids de la chose perpendiculaire à la surface et de signe opposé.
Décomposez donc, le poids en une composante perpendiculaire à la surface et une autre parallèle à la surface.
Au revoir.

[invite67e9590d]

Oui j'ai fait un dessin. J'ai décomposé (vecteur)R en (vecteur)Rn + (vecteur)f
C'est-à-dire la réaction perpendiculaire Rn et les frottements f. Comme f = 0 , on a alors (vecteur)P + (vecteur)Rn = m.(vecteur)a
Mais alors P = Rn donc m.(vecteur)a = 0 ...
Pourquoi décomposer le poids ?

[LPFR]

Re.
Relisez ce que j'ai écrit: Décomposez le poids en composantes (dans le dessin).
A+

[A voir en vidéo sur Futura]

[invite67e9590d]

J'ai décomposé P en P1 + P2 avec P2 perpendiculaire à la surface et P1 parallèle à celle-ci.
L'équation est alors P1 + P2 + Rn + f = ma
f= 0
et tan(x) = P2/P1
=> P1=tan(x).P2 = tan(x).mg
Donc mg + tan(x).mg - mg + 0 = ma
tan(x).mg = ma

Mais je n'ai pas utilisé le sinus...

[LPFR]

Re.
Arrêtez d'écrire des équations inutiles.
On ne les écrit que quand on sait le calcul que l'on veut faire.
Que vient faire 'f' alors que l'on vous a dit depuis le début qu'il n'y a pas de friction. Rajouter des termes inutiles tient du masochisme.
Cette équation
L'équation est alors P1 + P2 + Rn + f = ma
est idiote. Soit vous travaillez avec des vecteurs (en cas de masochisme en phase terminale) soit vous travaillez avec les seules composantes qui présentent un intérêt pour le problème.
Regardez les composantes du poids. Celle qui est perpendiculaire à la surface appuie sur la surface et crée la réaction. Les deux se compensent et ne font pas bouger la luge.
Il vous reste la composante le long de la surface. C'est elle qui accélère la luge et la seule qui intéresse ici.

Et maintenant regardez bien votre dessin et calculez la composante parallèle en fonction du poids et de l'angle.
Où se trouve l'angle droit? Qui est l'hypoténuse ?
A+

[aurelienbis]

Le calcul tient en une seule ligne. Si je peux te mettre sur la piste, il y a un sinus. Et la vitesse initiale ne sert à rien.

[invite67e9590d]

Je veux bien admettre que mon équation est inutile mais quand on ne comprend rien c'est toujours mieux d'essayer quelque chose plutôt que de ne rien faire...
En tout cas merci de prendre le temps de m'expliquer.
J'ai compris, par contre je trouve mg/sin(x) = ma et je devrais trouver mg.sin(x) = ma ...

Détails de mes calculs:
P = P1 + P2
P1 et R se compensent
donc P2 = ma
=> sin(x) = P/P2 = mg/P2
=> sin(x).P2 = mg
=> P2 = mg/sin(x)

Merci.

[invite67e9590d]

aurelienbis: je viens de voir ton message
Oui c'est ça mais j'ai du faire une erreur quelque part, je ne trouve pas...

[aurelienbis]

Encore plus simple que des calculs, fais un shéma. Il y a deux repères orthonormés : L'un R(x/y)(horizontal/vertical) et l'autre avec un angle de 12° par rapport à R ; R1(x1/y1).
g s'applique sur le repère R : -g.y
A toi de trouver la valeur de cette force selon x1.
C'est là qu'apparaît sin(x)*g.

[invite67e9590d]

C'est ce que j'ai fait, mais avec mg à la place de g, donc c'est pareil. Mais je ne trouve pas le bon résultat...

[aurelienbis]

Fais voir ton schéma.

[invite67e9590d]

En le refaisant à l'ordi, je viens de me rendre compte qu'en fait la décomposition du vecteur P est fausse

[interferences]

Bonjour,

En effet c'est mal parti.

Voilà une "méthode" pour trouver facilement et graphiquement la solution.

Première question : Quelle est la direction du mouvement?
Réponse : elle est donnée par la pente.
Deuxième questions : Quelles sont les forces qui travaillent?
Réponse : seul le poids travaille (l'autre est perpendiculaire au mouvement)
Troisième question : Comment trouver la composante du poids qui travaille?
Réponse : On prend une équerre et on la fait glisser le long de la direction du mouvement jusqu'au bout de la flèche du vecteur du poids.

On obtient alors le vecteur ma (remarque : si d'autres forces travaillaient alors on ferait la somme des composantes de ces forces qui travaillent).
Le reste est un simple problème de géométrie.

Au revoir

[invite67e9590d]

Excusez moi pour le retard, je n'ai pas pu venir plus tôt !
Merci beaucoup pour votre aide !

Bonne soirée

[lucas.gautheron]

Bonsoir,

n'hésite pas à nous faire part de tes résultats (pour vérification)

A+,