Stabilité d'une masse sur une butée

matilo · 28/04/2012 - 16h08

Bonjour, j’aimerais vous soumettre un pb de mécanique:
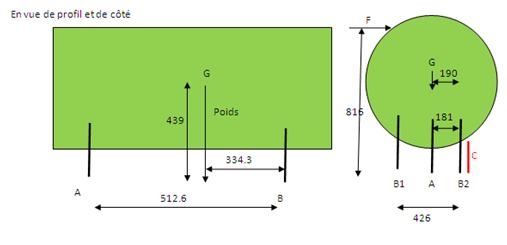
Soit une grosse masse M sur 3 pieds noté A, B1 et B2. B1 et B2 sont deux pieds à l’arrière. Schéma en joint
Je cherche la hauteur d’une butée de telle manière que la masse ne bascule pas si on applique une force F en négligeant les frottements.
Pb masse.JPG
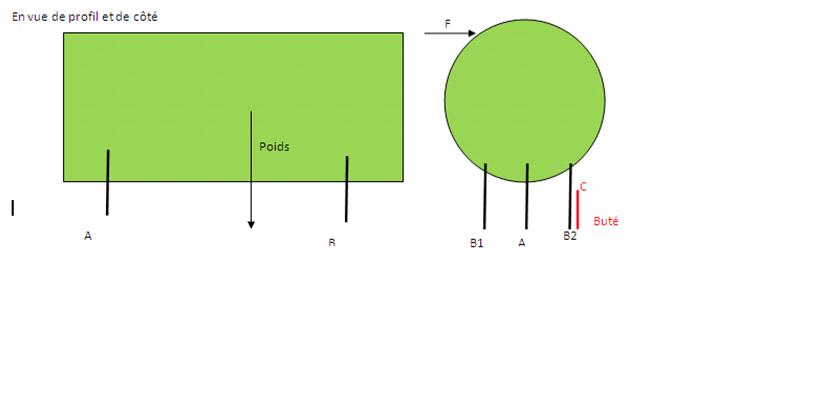
Cette butée est présente sur chaque pied.Je cherche la hauteur de cette butée. Je ne considère que le pied B2 en buté pour le calcul.
J’ai calculé le moment en C pour obtenir la hauteurde la buté rouge en disant qu’il y a basculement si B1=0. Dans le calcul du moment, je supprime le poids et je prends la répartition du poids sur A, B1, B2 (les valeurs donnant A+B-P=0)
Le raisonnement est bon ?
F a une valeur max Fmax
N’hésiter pas a donner votre raisonnement, c’est juste cela qui compte.

Schéma en joint
Merci

matilo · 29/04/2012 - 10h08

Quelqu'un?

Tifoc · 29/04/2012 - 10h49

Bonjour,
Votre problème est un peu difficile à concevoir clairement à travers le schéma donné... Il manque plein de cotes (en particulier la hauteur de la ligne d'action de F).
Si vous voulez une réponse précise, il faut décrire, avec plus de détails, ce que vous avez fait.
Vous pouvez calculer les moments en n'importe quel point (le centre de la Lune même, mais ce ne serait pas très malin

).
La condition de basculement B1=0 est ok. Par contre "je supprime le poids dans le calcul du moment" est une phrase qui m'inquiète...

matilo · 29/04/2012 - 11h14

Merci Tifoc,
Je n'ai volontairement pas mis les côtes.

Je me suis rendu compte que ma phrase est fausse: "je supprime le poids dans le calcul du moment"
Quand je fais mon moment en C, il me reste à la limite du basculement la force du sol sur la masse B1 et le poids P. C'est bien cela?
Connaissant la côte verticale d'application de la force F et la côte verticale de la force B1, je peux en déduire la hauteur de la butée.
Pour info:
A= 1218N
B1=314N
B2=336N
P=1870N
Pour les distance en considérant le schéma de droite: Z= verticale ascendante; Y=horizontale de gauche a droite

Distance horizontale suivant Y en mm:
CA 193,572
CB1 438,14
CB2 12
CG 201,959
CF 329,402
Finalement, la distance cherchée est CF suivant la vertical si je me trompe pas.

**LPFR** · 29/04/2012 - 12h09

Bonjour.
Avant de faire des calculs il faut comprendre comment se passerait le basculement de l'objet.
Quand le couple de la force augmente, les pattes B1 et A se "soulèvent" et tout le poids est supporté par B2.
Quand le milieu de la patte appuie sur la buttée, il y a une force horizontale du sol sur la patte B2 qui l'empêche de glisser vers la gauche.
Mais cette force horizontale dépend du coefficient de friction entre B2 et le sol, et évidement du poids.
C'est cet équilibre entre la force de friction et la force F qui détermine si la masse bascule ou non.
Au revoir

matilo · 29/04/2012 - 12h44

Merci LPFR,
Je suis tout a fait d'accord!
Par contre, je simplifie le pb en disant qu'il n'y a pas de frottement. (le pied a une bille par exemple).
Par contre, je pense que vous parlez du basculement de la masse sans butée.
Moi, j'imagine que le pied B2 est appuyé sur une butée de hauteur h que je cherche.
Si la force F est assez grande, au tout début du basculement, A et B1 s'annulent et on a une force en C.
Je me trompe?
Le moment de F en C va dépendre de la hauteur de la butée.
Du coup je reprends le raisonnement:
-En début de basculement, A et B1 nuls
-Je connais F et le Poids!
-Je recalcul B2 et la nouvelle force en C (butée sur patte) qui a des composantes verticale et horizontale.
L'angle de la force va dépendre du basculement de la masse et donc de la hauteur de la butée.
J'ai donc dans ce cas 4 inconnus: B2,C, l'angle de la force C: alpha et la hauteur de la buté qui détermine la distance CF
je pourrais dire qu'au debut du basculement, la force en C est presque horizontale et du coup, je n'ai pas d'angle et que B2 prend tout le poids. Du coup, j'ai 2 inconnues: la distance CF verticale et la force F
Je sais pas si je suis clair... peut etre tord!
Merci bcp!

**LPFR** · 29/04/2012 - 13h16

Re.
Non. Je parle du basculement avec la butée.
S'il n'y a pas de frottement, ni sur le pied ni sur la butée la force en C sera perpendiculaire à la patte B2.
Et la composante horizontale de cette force sera égale à F.
Donc, vous n'avez seule inconnue: F qui dépend de l'angle d'inclinaison. La composante verticale en C est donnée par F et l'angle d'inclinaison.
Pour l'équilibre il suffit de calculer les moments par rapport au pied.
A+

**obi76** · 29/04/2012 - 14h28

Bonjour,

évitez d'écrire en abrégé/SMS.

Pour la modération,

matilo · 29/04/2012 - 15h13

Merci
Mais le fait de dire que F est mon inconnue change le problème. Ma vraie inconnue est le hauteur de la butée puisque je souhaite trouver la valeur de h pour laquelle il y a basculement. Il peut n'y avoir aucun basculement si la force F n'est pas assez grande.Dans ce cas, je trouverai peut etre une hauteur nulle ou négative?? La force F, je l'ai déjà!

Je disais que j'avais plusieurs inconnues car je ne connais ni l'angle, ni la hauteur de la buté (que je cherche)!
et ni la force en C:
F-Csin (alpha)=0
B2-P-C cos (alpha)=0
moment en B2
-zF'*F+h*C+yG'*P=0
zF':distance B2F verticale
yG': distance B2G horizontale
C'est donc h que je cherche

Ai-je tord?
Merci pour le temps accordé

matilo · 29/04/2012 - 15h21

C'est donc h que je cherche. Je n'ai pas C sauf si je considère que B2 prend tout l'effort du poids.. mais cela donne C=0....je m'embrouille la

**LPFR** · 29/04/2012 - 17h02

Re.
C'est quoi alpha ? L'angle d'inclinaison ? Dans ce cas ce n'est pas
F-C sin(alpha)=0 mais F-C cos(alpha)=0
Et vous "trichez": les distances zF' et yG' dépendent de alpha. Vous ne pouvez pas les traiter comme des constantes.

Pour chaque angle d'inclinaison et pour chaque 'h' vous avec une force F d'équilibre.
Vous pouvez fixer 'h' et alpha et calculer F. Mais vous pouvez aussi fixer F et alpha et calculer 'h'.
A+

matilo · 29/04/2012 - 17h14

Le fait que les distances dépendent de alpha m'embete.
Car je considérais qu'on était à la limite du basculement donc avec un alpha proche de 0, ce qui faisait que les distances ne changent presque pas. Apres, quelles valeurs de alpha sont pertinentes: 0.2°, 5°....
Vu que je connais ma force F (qui est une donnée), j'aurais une infinité de valeurs de h suivant la valeur de alpha!

matilo · 29/04/2012 - 18h23

Je suppose que je ne peux pas faire une matrice de rotation autour de C pour avoir mes nouvelles coordonnées, car cela ferait décoller le point B2.
Pour relier les angles et les distances simplement.
Pour le point B2, sa coordonnée horizontale se deplace de tan (alpha)x'h'
Je sens que je dois me compliquer!

matilo · 29/04/2012 - 19h12

J'avoue être bloqué!

**LPFR** · 29/04/2012 - 19h30

Re.
Vous ne pouvez pas faire le calcul avec F constant et avec des conditions d'équilibre statique.
Car ce cas n'est possible que s' l'objet ne bascule pas (ou ne bouge pas).
Pour une hauteur donnée, calculez 'F' en fonction de la valeur d'alpha.
Quand F tombe à zéro, c'est le moment de basculement de l'objet.

Vous pouvez calculer aussi, pour quel angle F tombe à zéro en fonction de h.
A+