Bonjour,
Suite à une récente discussion portant sur les pendules j'avais suggéré à quelqu'un d'étudier le pendule de foucault.
LPFR ayant répondu que les calculs étaient lourds j'ai décidé de jeter un coup d'oeil sur l'article de wikipedia : http://fr.wikipedia.org/wiki/Pendule...le_de_Foucault
Je comprends bien l'idée cependant je ne suis pas d'accord avec les coordonnées de l'accélération de coriolis données.
On écrit queet
L'accélération de coriolis est
Ce qui d'après l'article donnerait :
Alors que je trouve l'exact opposé, c'est-à-dire :
J'ai l'impression que l'auteur de la démonstration a calculé l'accélération comme si on avait(mais ce ne serait pas cohérent avec la façon dont il a défini
plus haut)
Je ne vois pas où est l'erreur dans mon raisonnement (et il y a plus de chance que ce soit moi qui me trompe que l'auteur de l'article - et le produit vectoriel ne m'est pas familier).
Pouvez vous m'éclairez s'il vous plait ?
Merci.
A+,
-----





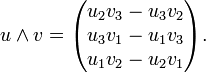

 Maintenant, on ne se demande plus si on va trouver un cours sur telle ou telle chose, mais plutôt comment choisir celui qui nous convient le mieux. Rien que pour la théorie quantique des champs, c'est une horreur tellement il y a de cours avec des approches différentes....
Maintenant, on ne se demande plus si on va trouver un cours sur telle ou telle chose, mais plutôt comment choisir celui qui nous convient le mieux. Rien que pour la théorie quantique des champs, c'est une horreur tellement il y a de cours avec des approches différentes....