Bonjour,
Nouveau sur ce forum, après l’avoir longtemps consulté sans m’inscrire, je viens à vous, car je suis devant un problème que je n’arrive pas à résoudre.
Je dois, dans le cadre d’une étude dimensionner un linteau type HEB pour l’installation d’une baie vitrée dans un mur porteur extérieur (la baie mesurera 1m40 de largeur)
J’ai calculé les descentes de charge qui influeront sur ce linteau soit 3394daN pour 1,4m ou 2424,6daN/ml=24246N/ml (merci pour les nombreuses discutions traitant ce sujet)
J’ai retrouvé pas mal d’info sur le forum qui pourraient m’y aider, mais je bloque entre toutes les infos que je retrouve, qui, comme je suis novice ne sont pas assez explicites, et, ce que je retrouve par ailleurs sur internet.
Je fais donc appel aux spécialistes (que je ne citerai pas mais qui se reconnaitront) pour m’apporter un peu d’eau à mon moulin.
Ce que j’ai compris (corrigez moi si je me trompe):
- Le linteau s’apparente à une poutre en appui libre aux extrémités.
- La charge est dite uniformément répartie.
- Il faut que je calcule la flèche, formule trouvée f=(5/384)x((Q.L^4)/(E.I)
- il faut (je crois) que je calcule le moment de flexion Mo=(Q.L²)/8=(24246N.1.4²)/8=5949mN mais je n’ai pas compris à qui cela servait.
J’ai trouvé d’autres formules pour les profilés :
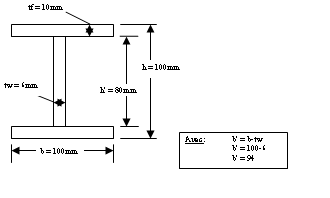
I=S.h²/2
I/v=S.h
Etc….
J’ai aussi trouvé sur ce forum cette démarche (Ce sujet date de 2010).
----------------------------------------------------------------------------------------------
Vérifications nécessaires :
Ceci étant dit, les critères à vérifier pour le dimensionnement de votre poutrelle sont :
1. Vérifier que la contrainte maximum ne dépasse pas une valeur admissible dépendant de l'acier choisit et des conditions d'utilisation.
2. Vérifier la stabilité de la poutre vis a vis du chargement considéré.
3. Estimer la flèche maxi et s'assurer qu'elle reste raisonnable (surtout pour des critères estétiques plus que mécanique)
4. Vérifier les liaisons aux extrémités.
Hypothèses :
Afin de faire un pré-dimensionnement rapide pour estimer quel genre de section vous avez besoin, je vais prendre les hypothèses suivantes :
1. Je prend comme acquis votre charge extérieure à P = 31 500 N s'appliquant de manière uniformément répartie sur la poutre.
Attention , cette hypothèse est extrêmement forte et une erreur d'analyse à ce niveau pourrait rendre les calculs qui suivent caduques...
2. Montage d'une poutrelle en acier de construction standard S235, de limite élastique Re = 225 MPa et de limite de rupture Rm = 340 MPa (valeurs issues de la norme NF 10025 sur les aciers de construction non alliés et un brut d'épaisseur compris entre 16 et 40mm)
3. Hypothèses de poutre en appuis simples à ses extrémités (hypothèses conservative se placant du côté de la sécurité)
4. Le Choix d'un coefficient de sécurité par rapport à la rupture de 3 semble vraiment le minimum pour ceux et celles qui vont habiter sous cette poutrelle.
Calcul avec HEB 180 :
1. Calcul de la contrainte :
Pour une poutre en appuis simples, la contrainte de flexion maximum vaut :
Sigma_flexion = (P*L/8 ) / (I/v) = (31500*6000/4) / (426000)=55,5MPa
Tau = P / S = 31 500 / 6530 =4,8Mpa
=> contrainte équivalente de comparaison = racine (sigma_flex² + 3*Tau²) = racine (55,5² + 3*4,8²) = 56,1 MPa
Compte tenu de notre critère de sécurité de 3 par rapport à la rupture, la contrainte admissible vaut :
Sigma_ad = Rm / 3 =340 / 3 = 113 MPa ....
Contrainte comparaison < sigma_ad
=>La poutre ne risque pas la rupture
2. Vérification de la stabilité :
Compte tenu de l'élancement de la poutre (6 mètres), cette dernière peut être sensible au phénomène de déversement.
En effet, sous la contrainte de flexion, la membrane comprimée va tendre à flamber dans son plan de plus grande inertie, entrainant avec elle le profilé.
La résolution précise d'un tel problème n'est pas trivial mais le calcul suivant en constitue une bonne approximation.
Soit S la section de la membrure comprimée. Dans le cas d'un HEB 180, cette section vaut S = 180 *14 = 2520 mm²
L'inertie de cette membrure dans son plan de plus grande résistance est :
I=e*b^3/12 = 14 * 180^3/12 = 6 804 000 mm^4
La charge critique de flambement d'EULER vaut alors pour une longueur L = 6000 mm :
Fcr = pi² * E * I / L² = pi²*210000*6804000 / 6000² = 391 725 N
On a vu au calcul précédent que la contrainte de flexion (et donc de compression dans la membrure comprimée) était de 55,5 MPa. Soit pour une section S = 2520 mm², équivalente à une charge de compression N = 55,5 * 2520 = 139 860 N
La stabilité est assurée si N < Fcr / 3. (le facteur 3 étant un critère de sécurité classique pour un pré dimensionnement)
=> poutre stable
3. Calcul de la flèche maximum :
La flèche maximum sera, avec la formule que vous avez utilisée, de l'ordre de :
f = 5/384 * PL^3 / (EI) = 5/384 * 31500*6000^3 / (210000 * 38310000)=11 mm.... soit environ L/500 ....
=>Déformée acceptable
Bilan:
A moins d'une erreur de calcul (ce qui est tout a fait possible), une poutre HEB 180 en acier S 235 uniformément chargée par un effort de 31 500 N convient parfaitement.
Ayant une marge de 2 par rapport dans le calcul de contrainte, je pense que l'on pourrait surement passer sur un profilé plus faible comme un HEB 100 ou un HEB 120 en faisant l'hypothèse d'une poutre bi encastrée et en calculant précisément les fixations vis a vis du moment d'encastrement. En effet, on gagne un facteur 2 sur la contrainte maxi et on abaisse aussi la valeur de la longueur utile pour le calcul d'instabilité.
Quelqu’un peut il me dire si cette méthode est bonne, si oui, pouvez vous m’expliquer comment on trouve le I/v (que veut dire I, et v, si l’autre formule I/v=S.h, h est la hauteur , mais S, c’est quoi, une surface en m² ???
D’ou vient cette formule: Sigma_flexion = (P*L/8 ) / (I/v)
Enfin bref, vous voyez que j’ai beaucoup de question, j’aimerais juste une démarche, des réponses simples, et détailler si vous le pouvez.
Je précise que c’est une étude, que cela ne sera jamais appliqué, mais au vu des différents sujets qui abordent ce problème, si quelqu’un veut bien prendre un peu de temps pour me répondre, cela aidera beaucoup de monde.
Je vous en remercie par avance
Cordialement
Steph.
-----





 !
! .
.