Exercice sur l'ARQS [CPGE]

[invite7f0a3eb8]

Bonsoir à vous ,

Voilà je rencontre des difficultés devant un exercice de physique , voici les problèmes :

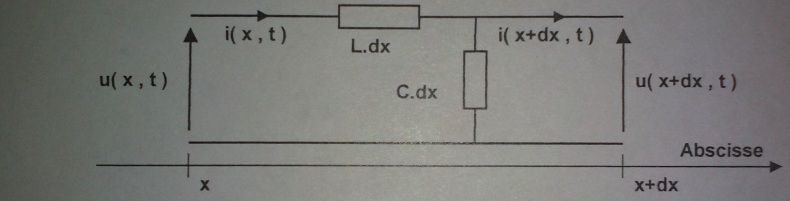
Le schéma de l'exercice est le suivant :

L est l'inductance par unité de longueur dx.
C est la capacité par unité de longueur dx.

1- Les lois de Kirchhof sont applicables. Etablir le système d'équations différentielles suivant :

du/dx = -L*(di/dt)
di/dx = -C*(du/dt)

Alors là , j'ai essayé de voir l'utilité des lois de Kirchhoff et je ne l'ai pas trouvée , puisque un unique courant et aucune résistance... J'ai bien pensé à U + Ul = 0 , avec Ul = L*(di/dt) , mais ensuite il faut prouver que U = du/dx ... Pour la deuxième , j'ai i = C*(du/dt) mais pareil je n'aboutis à rien. Pourtant , les égalités me semblent presque indispensables pour résoudre cette question.

2- En déduire l'équation suivante :

d²u/dx² - (1/v² * d²u/dt²) = 0 , où v sera exprimé en fonction de L et C.

Même en admettant la 1- , je n'y arrive pas. J'ai essayé plusieurs départs mais qui sont probablements faux. Cette idée de double variable ( Temps + Distance ) doit être ce qui m'embrouille le plus en fait...

3- Montrer que , pour une valeur définie de c :

u(x,t) = U+ cos[oméga(t-(x/c)] + U- cos[oméga(t+(x/c)] est solution du problème.

Là , c'est vraiment compliqué. Cette soudaine division de U en U+ et U- , je ne l'ai même pas comprise...

Je viens de voir l'heure et ça fait longtemps que j'y suis pour n'avoir presque aucun résultat. Un peu d'aide ne serait pas de refus.

Merci d'avance pour vos éclaircissements !

Lfcg.
-----

[DarK MaLaK]

Salut,

La pièce jointe n'a pas été validée, donc c'est dur de répondre à la question 1. Mais comme en physique, en général, les fonctions ne posent pas de problèmes, on a l'égalité : d²/dxdt=d²/dtdx. Donc je proposerais ça pour la question 2 :



Pour la dernière question, j'injecterais simplement la solution proposée dans l'équation différentielle obtenue à la question 2, pour montrer qu'elle la vérifie pour une valeur de c à déterminer. Je ne pense pas que les constantes U+ ou U- aient une importance.

[invite8d4af10e]

Bonjour
tu as le droit d’écrire : u(x,t)=Ul+Uc ( la bobine et le condo) sachant que c'est le même courant qui circule dans L et C .

[invite6dffde4c]

Bonjour.
Ce problème (écrit, de toute évidence, par un matheux) comporte un piège: C n'est pas une capacité et L n'est pas une inductance.
Par contre C.dx et L.dx sont bien une capacité et une inductance.
Votre première "loi de Kirchof" n'est autre chose que la définition d'une inductance:
U = L (dI/dt) soit, avec une inductance différentielle: du = (L.dx) (di/dt)
Même chose avec la seconde ligne. C'est la définition d'une capacité.
Remarquez que je ne mets pas des signes dans ce type d'équation. Ce sont des pièges à gogos.
On décide des signes avec le dessin du circuit à côté et avec les flèches indiquant le sens des courant et des tensions considérées comme positifs.

Je vous conseille de remplacer L et C, par des vraies inductances et capacités. Et d'en faire le calcul sans pièges et sans différentiels.
Puis, replacer les L par des L.dx et C par des C.dx.
Au revoir.

[A voir en vidéo sur Futura]

[stefjm]

Ce problème (écrit, de toute évidence, par un matheux) comporte un piège: C n'est pas une capacité et L n'est pas une inductance.

Pas si évident que cela...
Il a été écrit par quelqu'un qui préfère travailler par unité de longueur, c'est un choix clairement assumé dans l'énoncé.

Si je me souvient bien, en CGS (esu et emu), l'unité de l'inductance et du condensateur était le cm: Ça ne devait pas être simple de s'y retrouver.

[invite7f0a3eb8]

Merci à vous pour vos réponses !



XXXX pas d'images sur des serveurs externes XXXX


Voici le schéma du montage.

En fait dans la question 3 , je n'arrive pas à identifier les termes qui composent l'équation. " c " est la célérité des ondes ( Info donnée ) , t la variable de temps et x la variable de longueur. Mais d'où sort oméga minuscule ? Je n'ai aucune idée de comment le faire apparaître.