salut ,
voici un exo bien pertinent ,
l'orifice du récipient est relié à une canalisation horizontale , de longueur L , de section constante s , ( trés faible devant S du récipient), dans laquelle la vitesse du fluide , incompressible , est de la forme : v=v(x,t)ex , ex: vecteur unitaire,
à t=0, la vanne permettant le fluide de s'écouler est ouverte en B; la mise en vitesse du fluide est étudiée avec les hypothése:
* h varie trés peu,pendant la phase transitoire;
*l'accélération locale du fluide n'est importante que dans la canalisation est une petite région autour d'elle ,
1: montrer que la vitesse ne depend que de t dans la canalisation ,
voici que je ne sais d'où commencer !!!
merci ,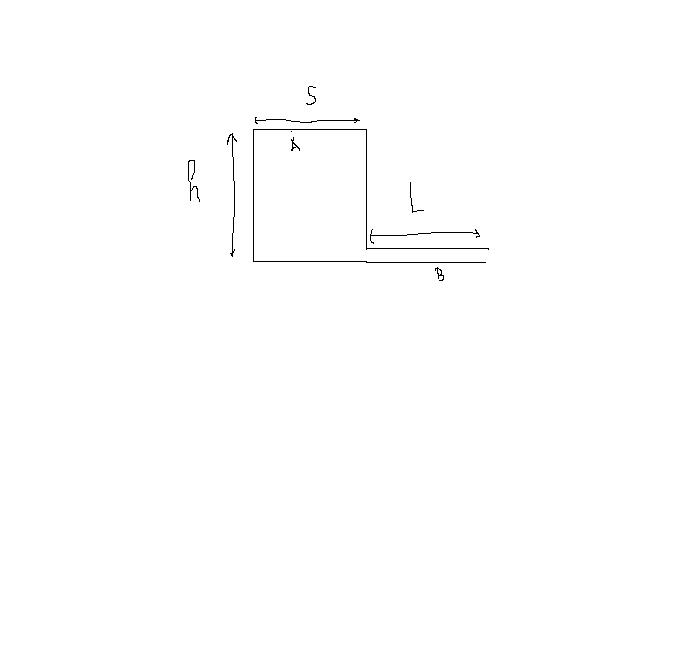
-----




