Problème d'optique géométrique

[jojo399]

Bonsoir, je ne parviens pas à comprendre cet exercice (un qcm) et j'espère que vous pourrez m'aider.
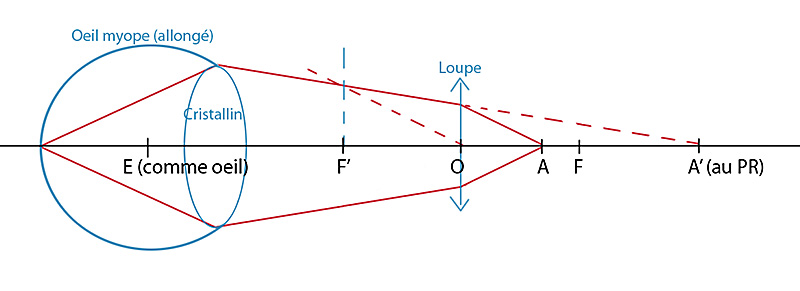
"Un bijoutier et son assistant travaillent alternativement sur le même établi. Les travaux de précision s'éffectuent sous une loupe convergente de 4,5 dioptries à hauteur réglable. La distance oeil-objet est de 50cm et les deux artisans cherchent chacun un réglage leur permettant de travailler sans accomoder. Le bijoutier à une myopie de 1 doptrie alors que son assistant est émmétrope."
A. Dans les deux cas, l'image de l'objet au travers de la lentille se trouve au ponctum remotum de l'oeil de l'artisan.
-> là pas de pb, c'est vrai, par définition pour qu'une image soit nette elle doit être formée sur le PR
B idem
C l'assistant doit placer la lentille à 2/9ème de mètre de l'objet
-> c'est vrai aussi, en utilisant la formule de conjugaison (qui est la seule donnée sur ce chapitre) : 1/OA' = 1/OF + 1/OF' = 2/9 + (-4,5) = 0 donc pr à l'infini

enfin on demande où le patron doit placer la lentille, la réponse est à 1/6ème de mètre de l'objet mais je ne trouve pas comment faire ...
En vous remerciant par avance,
Bonne soirée
-----

[Pixelvore]

Bonjour,

Avant toute chose, on calcule le PR du binoclard, qui n'est pas à l'infini : une lentille divergente de 1 dioptrie corrige sa vision de loin i.e lui permet de regarder à l'infini : des rayons arrivent de l'infini, divergent un peu en passant le verre des lunettes, puis en passant par le cristallin convergent en un point pas flou sur la rétine. Ca veut dire que le verre correctif seul transforme l'infini en le punctum remotum du myope, et donc que le PR est simplement l'inverse de la correction en dyoptrie (valeur absolue pour être précis). Si ça paraît pas évident, faire un dessin, ça le deviendra Donc dans notre cas, le patron voit net au maximum à 1/1dioptrie = 1m.

Maintenant les choses sérieuses :



Tout y est, y'a plus qu'à : on cherche OA, donc comme on sait conjuguer OA à OA' cherchons d'abord OA' :
OA' = OA + AE + EA' = OA - distance oeil->objet + PR du patron = OA - 1/2 + 1 (je passe en calculs semi-numériques pour pas m'embêter... A ne pas faire dans un devoir, conserver les grandeurs littérales jusqu'au bout )
Puis conjugaison de A et A' : 1/OA' - 1/OA = 1/OF' = -1/f' <=> 1/(OA+1/2) - 1/OA = -9/2
Puis on résout, j'ai vérifié ça donne OA = 1/6 de mètre en effet.

[edit] oui je sais j'aurais au moins pu dessiner l'iris plutôt que de faire s'engouffrer toute la lumière dans l'oeil. Le pauvre patron va se griller la rétine

[jojo399]

Merci tout d'abord pour ta réponse, certains points continuent cependant à me poser pb :

cherchons d'abord OA' :
OA' = OA + AE + EA' = OA - distance oeil->objet + PR du patron = OA - 1/2 + 1

Je ne comprends pas comment tu trouves ce calcul, même avec des shémas
Par ailleurs j'ai vu comment tu traduisais la myopie de 1 dipotrie et je me demande du coup comment on traduirait une hypermétropie de 1 dioptrie ?
Merci de ta patience,
Bonne journée

[Pixelvore]

Euh... La 1è égalité est juste une relation de Chasles. Je n'ai pas pu écrire les "barres" au-dessus des longueurs comme on le fait d'habitude en optique géométrique pour symboliser des longueurs algébriques, comptées positivement vers la droite et négativement vers la gauche. Par exemple si A et B sont à 1m l'un de l'autre avec A à gauche, AB = 1m, BA = -1m. Du coup on peut écrire des relations de Chasles comme on le fait sur des vecteurs en 2D ou en 3D (là on a des vecteurs 1D en fait, collés sur une droite).
Ensuite la 2è égalité ben je remplace les termes par ce que je connais : AE est la distance oeil->objet qui est une donnée de l'énoncé, et EA' est la distance oeil->(image de A par la loupe) et comme l'image de A par la loupe doit être au PR pour le type, EA' = PR.
Ouais ou pas ouais ?

Pour ce qui est de l'hypermétropie, on peut faire le même raisonnement que pour la myopie mais cette fois ça se passe au PP et pas au PR : le PR de l'hypermétrope est toujours à l'infini (il est même "derrière" l'infini si tu vois ce que je veux dire : il a besoin d'accomoder pour voir à l'infini, à l'inverse au repos il est même capable de former une image ponctuelle à partir de rayons convergents), mais en revanche le PP est repoussé : l'hypermétrope ne voit pas bien de près. On pourrait trouver une relation entre le PP emmétrope, hypermétrope, et la focale du verre correctif, mais la relation ne sera pas aussi simple que pour la myopie : dans le cas de la myopie ça se passait bien car quand on en arrive à la conclusion "le verre correctif transforme l'infini en le PR", c'est cool car c'est justement la définition de la distance focale du verre. Par contre pour l'hypermétropie, on ferait un dessin et on pourrait juste constater que le verre correctif a pour effet de ramener le PP hypermétrope au PP emmétrope. Pas de relation évidente avec la distance focale donc, faudrait poser l'exo proprement

[A voir en vidéo sur Futura]

[Pixelvore]

[edit tardif] ah mais oui en fait je viens de tilter sur mes dernières phrases : autant pour la myopie on avait 1/PR' - 1/PR = 1/f' et comme 1/PR = 0, PR' = f', autant là on a simplement 1/PP' - 1/PP = 1/f'... Ce qui donne, si PP' = PP (oeil emmétrope qui n'a donc pas besoin de correction) 1/f' = 0 dyoptrie, bref un verre neutre.

[jojo399]

Ok ! il me semblait bien que ça ressemblait à une relation de chasles, mais comme la méthode n'a pas du tout était évoquée en cours et que je n'en n'avais pas vu depuis le lycée... bref, c'est bien clair maintenant : merci !
En fait en reprenant la correction (très succincte) du prof il raisonne en partant du résultat (vu que ceux sont des qcm) ce qui évite cette étape : il part de OA et trouve que le PR (EA') est bien là où il doit. (je dis ça juste pour info)
En tout cas encore merci et à bientôt.