Simulation de choc (chute libre)

[epsylone25]

Bonjour,

Tout d'abord bonne année et meilleurs voeux à tous.

Pour mon travail actuel, j'essaie de modéliser le choc d'un objet sur une surface après une chute supposée libre.

L'objet est un cylindre (diamètre 4cm, hauteur 0.5cm) en laiton tombant d'une hauteur de 1m sur une surface en téflon.


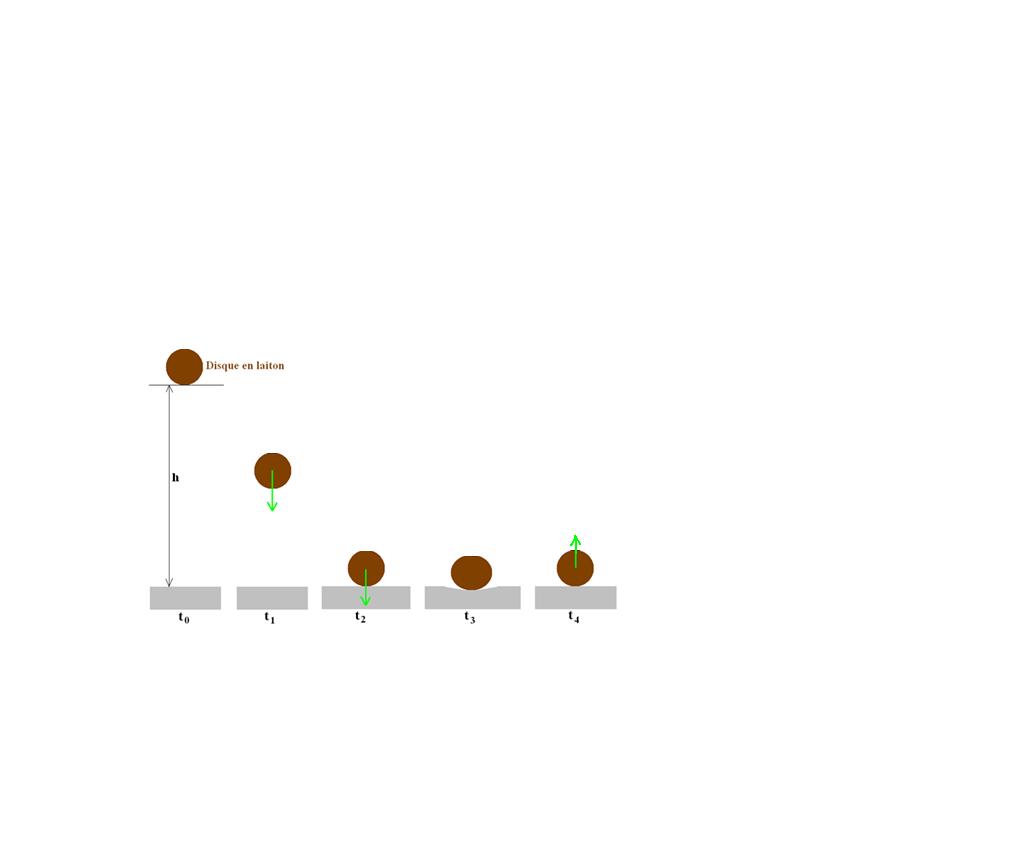
Ce qui m'interesse est le choc, c'est à dire la durée entre t2 et t4 sur le dessin ci-dessus.
Ce que j'aimerai déterminer :
- la décélération max du cylindre exprimé en [g] (9.81m/s2)
- la contrainte [N] (force) subit par le cylindre
- l'énergie [J] à dissiper lors du choc

(ces 3 notions sont certainement liées mais je ne sais pas trop comment)

Comme je peux calculer la vitesse à l'impact (racine 2*g*h), je peux calculer une décélération moyenne si je connais le temps de décélération (mais cette valeur ne m'interesse pas).
Pour ce qui est demandé, je pense qu'il faut faire intervenir les modules de Young (contrainte partiellement elastique) car la matière va se déformer.

En faisant des recherches sur internet, je n'arrive pas à trouver une relation liant la vitesse, l'accélération, la matière, masse, énergie ?...
Comme vous le voyez, tout n'est pas claire dans ma tête et je m'excuse d'avance si y a des erreurs dans ce qui est dit.
J'espère avoir un peu d'aide afin de mieux comprendre.

Merci.
-----

[LPFR]

Bonjour.
Si on suppose que c'est uniquement le téflon qui se déforme et que le problème est presque statique (pas d'ondes mécaniques dans le téflon ou le palet), la relation qu'il vous faut est la force sur le palet en fonction de la déformation du téflon.
Mais même pour cela il vous faut un foriste qui se connaisse en RDM, comme notre ami Jaunin, que je salue.
Car le problème n'est pas simple. La forme de la surface déformée du téflon reste à déterminer. Elle n'épouse le palet qu'à l'endroit de contact, mais elle se déforme aussi aux abords de la surface de contact.
Au revoir.

[epsylone25]

Merci de la réponse, il est vrai que le problème devient plus simple, mais même en le simplifiant ainsi je ne sais pas trop comment le résoudre.

De plus, je pense qu'en négligent la déformation du laiton, on fausse "pas mal" les calculs, en effet, le laiton est une matière "relativement" molle.
Si c'était du diamand, ok, on pourrait peut être négliger.
De plus j'espère pouvoir appliquer ce model à de l'or (à la place du laiton) qui est encore plus mou ...

Sinon une autre question me vient à l'esprit :
Dans le cas inverse où c'est le téflon (un morceau de 20x20x20cm par exemple) qui vient frapper le cylindre, pensez vous que le choc serait pareil (que le cylindre qui tombe sur le téflon) ?
Evidemment on suppose la même vitesse à l'impact.
Mais ici au lieu d'une chute libre, ça serait un mouvement de translation "horizontal" où on néglige les frottements.

[LPFR]

Re.
De toute façon il faut attendre que Jaunin passe par ici.
Que le choc soit dans un sens ou dan l'autre ne change rien.
Par contre ce qui change est que dans votre dessin vous avez placé le téflon sur du dur (la pari du bas ne se déforme pas. Si elle n'est pas "dure" alors ça change tout.
La supposition que c'est le téflon qui se déforme et non le laiton est très raisonnable. Le module de Young du téflon est de 0,5 GPa, alors que celui du laiton est de 100-120 GPa. Tenir compte de la déformation du laiton ne changera pas grand chose au résultat.
A+

[A voir en vidéo sur Futura]

[epsylone25]

Merci à Jaunin pour les 2 documents qu'il m'a envoyé.
Le plus dur est à venir : comprendre ce qui est écrit
Quand LPFR disait que c'était pas simple, il voulait dire que c'est monstre compliqué ^(•.•)^.

[Jaunin]

Bonjour, Epsylone25,
Pourriez-vous nous en dire plus, si c'est possible, confidentialité, sur les fonctions de votre système, car comme on peut changer l'ordre des fonctions du téflon, par exemple.
D'autre part, juste comme ça, qu'est ce qui nous garanti que le cylindre tombe bien horizontalement ou qu'il ne rebondit pas en dehors de la plaque de téflon.
Plusieurs cylinres peuvent tombés presque en même temps ?
Qui ou quoi ramasse les cylindres ?
En autre, etc.
Cordialement.
Jaunin__

[epsylone25]

Bonjour Jaunin,

J'ai choisi le cylindre laiton car il ressemble au pièces qu'on fabrique, rien ne garanti qu'il tombe "correctement" dans la réalité car selon comment l'utilisateur lache l'objet (involontairement), celui ci tombe aléatoirement.

Néanmoins nous avons un système simulant un choc reproductible (vitesse impact constant, direction choc défini, ...), le problème est que nous ne somme pas sûr de nos mesures avec accéléromètre+ampli+osclillosc ope (les valeurs semblent très élevées, 5000g pour une chute libre de 10cm d'un cylindre laiton de 63g).
Ainsi on a cherché à comparer nos valeurs par rapport à un modèle théorique afin de voir si on est à "coté de la plaque" ...
Les matières et géométries peuvent être adaptés selon besoin.

Mais il faut avant tout comprendre ... et c'est ici que je suis bloqué ..., j'ai commencé à lire les 2 documents que vous m'avez envoyé (encore merci), et j'avoue avoir un peu de mal avec toutes ces formules sur +150 pages ...
S'il existait un exemple ressemblant à notre situation, je suis preneur (c'est plus simple qu'apprendre toute la théorie des chocs... ça risque d'être long ...)

Le but de ces tests et de voir les dégats subit par notre pièce, ainsi on veut connaitre la contrainte et donc l'accélération max subit pendant le choc.

Cordialement.

[Jaunin]

Bonjour, Epsylone25,
Avez-vous regardé ce lien, c'est le teste effectué en horlogerie pour la chute d'une montre.
Cordialement.
Jaunin__

http://forums.futura-sciences.com/ph...cs-5000-g.html

[Jaunin]

Bonjour, Epsylone25,
Avez-vous bien pris en compte la longueur des câbles des accéléromètres, car de mon temps lors de mesures ces derniers nous créaient beaucoups de soucis dans les mesures.
Je vous joins un document en MP.
Cordialement.
Jaunin__

[chaverondier]

J'essaie de modéliser le choc d'un objet sur une surface après une chute supposée libre.

je n'arrive pas à trouver une relation liant la vitesse, l'accélération, la matière, masse, énergie ?

D'abord, si
P est le poids de l'objet
R le rayon du cylindre et M sa masse
h la hauteur de sa chute
k la raideur de contact acier sur téflon (calculée en négligeant la souplesse de l'acier)

l'effort maximal F = kx d'écrasement du ressort vérifie
1/2 kx² = P(h+x) soit kx² -2 Px - 2 ph = 0
d'où
F = kx = P + (P² + 2kPh)^(1/2) (1)

Par ailleurs, dans l'hypothèse d'un milieu en téflon semi-infini on trouve, par intégration de 0 à +00 des souplesses dk = dx/(EA) de couches successives "d'épaisseur dx" du "cône de diffusion à 45°" de l'effort de compression dans le téflon, on trouve une raideur de contact cylindre sur téflon valant (si je me souviens d'un calcul que j'avais fait il y a 5 ans 1/2 et dont j'ai la flemme de réécrire les 2 lignes)

k = E (pi A0)^(1/2)

E étant le module de Young du téflon
A0 = pi R² la surface de téflon impactée,
la surface du cône de diffusion à 45° comprimée à la profondeur x valant A = pi (R+2x)²
(diffusion à 45° de l'effort de compression)

La formule (1) ci-dessus devrait, je pense, marcher à peu près (sachant que, quand même, on néglige ainsi l'inertie du téflon dans cette approche dynamique simple à 1 ddl)

[epsylone25]

Tout d'abord merci pour les réponses , et surtout un gros gros merci à Jaunin pour son aide et ses documents .
Je vais lire tous ça et essayer de l'appliquer à mon besoin.
J'ai bon espoire ce coup ci !

Merci.

[epsylone25]

Une petite question par rapport à la formule : k = E (pi A0)^(1/2) (1)
c'est très difficile de déterminer A0 dans mon cas...
Ainsi pour palier à ce problème je passe par le modèle ressort qui donne une sinusoide, on obtient :
T=2.Pi.(m/k)^1/2.
Comme je peux déterminer T (=2 fois la durée du choc), j'en déduis k.
Est ce que la raideur k calculé ainsi correspond à la raideur k calculé selon (1) ?

Ainsi connaissant k, je peux déterminer F et x avec F = kx = P + (P² + 2kPh)^(1/2).
Connaissant F, j'en déduit l'accélération max (F=m.a)

Est ce correct de faire ainsi?

[chaverondier]

Une petite question par rapport à la formule : k = E (pi A0)^(1/2) (1)
c'est très difficile de déterminer A0 dans mon cas...
Ainsi pour palier à ce problème je passe par le modèle ressort qui donne une sinusoïde, on obtient :
T=2.Pi.(m/k)^1/2.
Comme je peux déterminer T (= 4 fois la durée du choc), j'en déduis k.
Est-ce que la raideur k calculée ainsi correspond à la raideur k calculé selon (1) ?

1/ Oui si toutefois la réaction R pendant le choc est bien proportionnelle à l'enfoncement x (R = k x)

2/ Si, au contraire, on a une loi réaction d'appui/enfoncement de type système à seuil de valeur F0 (modèle adapté au cas où le cylindre tombe à plat sur un matériau à comportement plastique) alors, P désignant le poids et h la hauteur de chute, on a (énergie fournie par la pesanteur = énergie absorbée par le travail résistant de la réaction d'appui F0 pendant l'enfoncement x)

P(h+x) = F0 x d’où x = Ph/(F0-P) (pas de solution physique si F0 ne supporte pas le poids P)

3/ Si le téflon réagit comme un matériau plastique, avec un seuil plastique constant p0 et que l'on tombe sur un "coin du cylindre", alors la réaction R augmente comme la surface projetée du coin de cylindre qui s'enfonce dans le téflon. Dans ce cas, on devrait avoir une loi de réaction sensiblement en

R = C x^3/2

En effet,
si alpha désigne l’inclinaison de l’axe du cylindre par rapport à la verticale,
si 2b désigne la longueur d'arête circulaire du cylindre pénétrant d’une profondeur x dans le téflon,

la 1/2 longueur b vérifie sensiblement : x/sin(alpha) = b²/(2r) (comme la parabole osculatrice de hauteur x/sin(alpha) d’un cercle de rayon r)
la largeur d'empreinte est égale quant à elle à x/sin(alpha) + x/cos(alpha)

On a donc
R = 2 p0 [x/sin (alpha) + x/cos(alpha)] [2r x/sin(alpha)]^1/2, d'où R = C x^3/2 avec
C = 2 p0 [1/sin(alpha)+1/cos(alpha)] [2r/sin(alpha)]^(1/2), on a alors

P(h+x) = 2 C x^(5/2)/5, soit encore x = [5 P(h+x)/(2C)]^(2/5)

valeur très voisine de : x1 = [5 Ph/(2C)]^(2/5)

Si on se trouvait dans un cas où l’enfoncement x ne pourrait pas être négligé devant la hauteur de chute h, la première itération devrait suffire et dans ce cas :
x = [5 P (h+x1)/(2C)]^(2/5)

4/ Si on a une loi réaction d'appui/enfoncement de type R = C x²
(par exemple, si l'écrasement relatif epsilon s'avère être proportionnel à l'enfoncement x et que le matériau amortissant le choc a un comportement de type sigma = E epsilon^(1/2)) alors

P(h+x) = C x^3/3 soit encore x^3 – P x/C – Ph/C = 0,

Posons p’ = P/(3C) et q’ = Ph/(2C) et D = q’² - p’^3

Le déterminant D de l’équation du 3ème degré reste positif si

P²h²/(4 C²) > P^3/(27 C^3) soit C h² > 4 P/27 (hauteur de chute suffisante) et on a alors

x = [q’ + D^(1/2)]^(1/3) + [q’- D^(1/2)]^(1/3)

5/ Dans le cas d’une réaction de type R = C x^3, la balance d'énergie nous donne cette fois-ci une équation du 4ème degré en x

P(h+x) = C x^4/4

On peut encore exprimer analytiquement le résultat de cette équation du 4ème degré en décomposant le polynôme d'ordre 4,

P4 = x^4 - 4Px/C - 4Ph/C en un produit de deux polynômes de degré 2 : P4 = (x² + b x + b²/2+a) (x² - b x + b²/2 - a) avec

(b²/2 - a)(b²/2 + a) = - 4Ph/C et b(b²/2 - a) – b(b²/2 + a) = - 4P/C, soit

b^4/4 –a² = -4Ph/C et ba = 2P/C d’où b²a² = 4 P²/C². En posant B = b²/2, on obtient

a² = B² + 4Ph/C et 2B (B² + 4Ph/C) = 4 P²/C² soit B^3 + 4 B Ph/C – 2P²/C² = 0

Pour résoudre cette équation du 3ème degré en B, on l’écrit sous la forme

B^3 – 3 p’ B – 2 q’ = 0, on pose donc p’ = – 4Ph/(3C) q’ = P²/C² et D = q’² - p’^3 = (P/C)^4 + [4 P h/(3 C)]^3 > 0

Le déterminant D est positif. L’équation du 3ème degré en B possède une seule racine réelle

B = [q’ + D^(1/2)]^(1/3) + [q’ - D^(1/2)]^(1/3) on a alors

b = +/-(2 B)^(1/2) et a = 2P/(C b) et on en tire les 4 solutions de l’équation du 4ème degré en x.

[epsylone25]

Ah ok, c'est plus compliqué que ça ^^.

La relation R=k.x implique que la réaction est linéaire par rapport à l'enfoncement.
Mais apparement ça dépend du matériaux, de façon général on a R=k.x^i

Comme je ne sais pas du tout comment se comporte l'enfoncement par rapport à la réaction, je suis donc mal baré .
J'espère que cela suis R=k.x pour du téflon et du bois...

Merci pour vos réponses en tout cas !

[ogust]

c'est quoi la chute libre

[epsylone25]

Une chute dont on néglige les frottements avec l'air.
Ca permet de simplifier les problèmes et ça marche plutot bien si la hauteur de chute n'est pas trop importante.

[Jaunin]

Bonjour, Epsylone25,
J'ai essayé une recherche sur le coefficient de restitution du Téflon, c'est pas évident.
Je vous joins ce que j'ai trouvé, en espérent que vous trouviez une information valable.
Cordialement.
Jaunin__

http://www-physique.u-strasbg.fr/~ud...ff_restit.html
http://ntrs.nasa.gov/archive/nasa/ca...2005194982.pdf
http://www.fast.u-psud.fr/~gondret/POF2002.pdf
http://www.om.ugal.ro/AnnalsFasc8Tri...9-Irimescu.pdf

[chaverondier]

Ah ok, c'est plus compliqué que ça ^^.
La relation R=k.x implique que la réaction est linéaire par rapport à l'enfoncement.
Mais apparemment ça dépend du matériau !

Pas seulement du matériau. Ca dépend du matériau et de la surface impactée. Pour le cas d'un cylindre qui tombe sur un coin, j'ai donné (dans mon précédent message) une proposition de type R = C x^(5/2) (en donnant la formule de calcul de C) correspondant au cas d'un comportement du matériau parfaitement plastique de la surface plane impactée (et supposé nettement plus mou que le matériau dont est formé le cylindre).

Par ailleurs en proposant (dans votre réponse à mon premier message) une période du système masse ressort T = 2 fois le temps d'impact quand la réaction est de type R = k x, c'est vous qui aviez raison. Dans le cas d'une réponse linéaire de type R = k x, T/4 est le temps pendant lequel l'enfoncement x augmente. T/4 est donc seulement la moitié de la durée du choc (le contact dure bien T/2 dans le cas d'une réponse de type R = k x).

[Jaunin]

Bonjour, Epsylone25,
Dans le temps il y avait ça, je ne sais pas comment ça a évolué, c'est peut être ce que vous utilisez maintenant.
Cordialement.
Jaunin__

http://www.ssc.ch/d2wfiles/document/...Shocks203D.pdf

[epsylone25]

Merci pour toutes vos infos

Je vois le bout du tunnel ce coup-ci, mes mesures correspondent enfin aux 2 models (simplifié) théoriques.
Je pense avoir compris les grandes lignes, et c'est suffisant pour faire ce que je dois faire.

Ce forum est une mine d'informations et un super moyen d'échanger nos connaissances.

Un gros gros merci à Jaunin et à Chaverondier pour leur aide