Salut tous,
j'ai une question assez basique mais j'ai un petit blocage. J'ai une grandeur physique "A" qui à une valeur connue dans un syst. axe cartesien (ds 2directions x et y)
et je veux connaitre cette grandeur pour un angle quelconque.
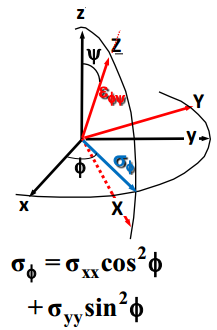
j'ai regardé mon cours et j'ai trouvé :
cette expression m'a un peu étonné car d'apres mes (vieux) souvenir de trigo ce genre d'expression ne me dit rien.
j'ai donc essayé de retrouver ceci mais je n'y arrive pas, pourriez vous m'aider svp ?
Bonjour,
Si vous êtes en deux dimensions, c'est facile, un petit dessin et c'est plié.
En trois dimensions, il faut définir proprement les deux repères et s'il n'y a pas de relations simple entre les deux (par exemple un axe commun, mais on revient à 2D dans ce cas), écrire la matrice de rotation qui permet de passer d'un repère à l'autre (on a besoin de l'axe de rotation et de l'angle).
@+
ps : sans le schéma qui va avec, je ne prend pas le risque d'interptéter votre formule (qui me semble fausse de toute façon, mais comme je disais, sans dessin je peux dire une connerie !).
Dernière modification par albanxiii ; 28/03/2013 à 12h02.
Not only is it not right, it's not even wrong!
merci beaucoup d'avoir pris le temps de repondre.
voici en pièce jointe un petit schéma du cours (le sigma sur le dessin représente le "A" dans mon texte)
merci pour ton aide
Re,
Merci pour le schéma.
Siet
Comme une telle erreur a une probabilité très très faible de se produire dans un livre / cours, la question est donc : de quoi
@+
Not only is it not right, it's not even wrong!
salut et merci pour ton aide !
pour avoir
je pense que ça doit venir d'ici le fait qu'on est cette relation bizarre
j'ai oublié de dire : toutes les composantes sont nulles à priori sauf la diagonale
