Bonjour,
J'ai un petit soucis d'écriture des fonctions de transfert dans le cas d'utilisation du théorème de superposition pour les systèmes linéaires.
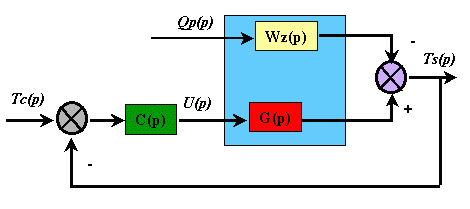
Soient les fonctions de transfert
entre
et
avec
nulle
et
entre
et
avec
nulle
La superposition donne :
Jusque là, pas trop de soucis.
Là où cela devient ennuyeux : On remplace G1 et G2 et cela donne :
Et bien évidement, il ne faut surtout pas simplifier bien que l'abus d'écriture utilisé (et évidement pas expliqué aux élèves) le permet...
Pour mon cas, je m'en sors en utilisant le bon symbolisme mathématique
Cependant, c'est quand même un peu lourd...
Verriez-vous une solution plus élégante, plus facile?
Cordialement.
-----