Estimation de l'énergie cinétique acquise par un projectile dans un pistolet magnétique

[invite52dd35ad]

Bonsoir à tous,


Quand j'étais petit, je voulais faire un espèce de "pistolet magnétique".
J'y ai re-pensé y'a pas longtemps, et donc j'aimerais bien voir si c'est possible avec seulement... des aimants !

Le système de base, juste pour se visualiser la question, est décrit ici :
Pièce jointe 237709

Je dessine très mal, donc je l'explique.


L'aimant de gauche est fixe.
Etape 0 : Les aimants, le projectile et le clapet sont dans la configuration de l'image.
Etape 1 : Le clapet s'abaisse.
Etape 2 : L'aimant libre est repoussé par l'aimant fixe et entraîne le projectile avec lui.
Etape 3 : L'aimant libre est arrêté par le fil et le projectile est éjecté hors du pistolet.

(Oui, ça fait un truc où on doit recharger à chaque tir)

La question, c'est comment calculer l'énergie cinétique acquise par le projectile ?
Pour commencer, je néglige les frottements de l'air, ceux entre l'aimant et le canon, ceux entre le projectile et le canon et la tension du fil lorsqu'il n'est pas totalement tendu.

À partir de là, connaissant la vitesse de l'aimant libre en fin de course, on a directement l'énergie cinétique du projectile, étant donnée que la vitesse de l'aimant égale celle du projectile.
Soit E_cp = (1/2)m_p*v_al²
Avec :
E_cp l'énergie cinétique du projectile. m_p la masse du projectile. v_al la vitesse de l'aimant libre en fin de course.

Ou alors, directement en fonction de E_cal et m_al, on a :
E_cp = (m_p/m_al)*E_cal/m_al


Il faut donc calculer l'énergie cinétique de l'aimant libre en fin de course.

Le problème, c'est que je ne connais /absolument rien/ au magnétisme.

Déjà, les deux aimants sont identiques. À partir de là, mes non-connaissances me disent que y'a un moyen de définir un "champ de potentiel magnétique" (je n'ai aucune idée concernant l'existence de ce concept).
De cette manière, pour obtenir l'énergie cinétique de l'aimant en fin de course, il suffit de calculer la différence entre son énergie potentielle en début de course et en fin de course.

Etant donné le système symétrique par rapport à l'axe passant par le centre des deux aimants, on peut dire que "l'énergie potentielle magnétique" de l'aimant libre ne dépend que de la distance des centres des deux aimants.
On dit que cette énergie potentielle est nulle lorsque l'aimant libre est à l'infini.
Je suppose qu'elle est décroissante et qu'elle ne dépend que d'un paramètre caractéristique lié à l'aimant.

Pour l'instant, juste pour pouvoir continuer le raisonnement et en attendant que vous me corrigiez, je la modéliserai par E_pal= m_al*A/d
Où A est le paramètre caractéristique lié à l'aimant et d la distance entre les deux aimants.
On a donc au final :
E_cal = E_pal(l = li) - E_pal(l = lf)

Maintenant, l'autre problème, c'est de déterminer le paramètre "A".
Je suis allé sur un site (je ne mets pas lien pour éviter la pub) pour trouver un aimant, et voici ses caractéristiques :
Cylindrique, épaisseur de 20mm et "Force d'adhérence ~ 38 kg" avec à côté un graph' légendé "Force d'adhérence en fonction de la distance entre l'aimant et son support métallique."
Et pour une distance de 0, on a 38kg. Soit à 10mm du centre de l'aimant en fait (20mm d'épaisseur / 2)

Le problème, c'est que je ne sais pas si sans connaître le matériau du "support métallique", il est possible de déterminer A.


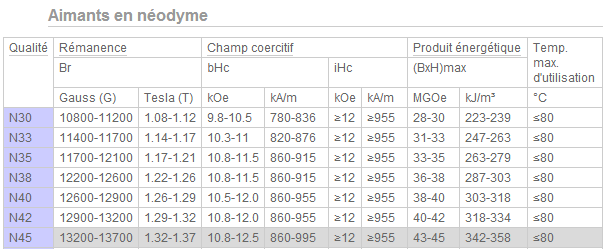
En fait, le site met à disposition un tableau de valeur, et j'ai donc ceci :



Celui sur lequel je me concentre est le N45, et je n'ai strictement aucune idée d'à quoi correspondent toutes ces valeurs

Voili voilou, si vous pouviez m'aider, ce serait très sympa !

Sur ce, bonne soirée et bonne année 2014 !
-----

[LPFR]

Bonjour.
L'image n'est pas visible. Même pas avec mes "superpouvoirs".

Mais pour une fois, le fait que vous ne connaissiez pas le magnétisme ne change rien. Même en le connaissant on ne peut pas calculer ce que vous voulez.
Le seul cas dans lequel on peut faire des calculs approchés est quand les deux aimants sont très proches (une distance plus faible que les diamètres. Dans tous les autres cas, on ne peut pas calculer le champ en fonction de la position de l'autre aimant. Et donc, votre "l'énergie potentielle magnétique" n'est aps calculable. Du moins pas analytiquement. Il faut utiliser un logiciel adapté. Peut-être le logiciel gratuit FEMM, mais il n'est aps adaptée aux aimants et il est 2D.

La seule chose que je peux vous donner, et ce n'est qu'une approximation pour une distance inférieure au diamètre des aimants est une force égale à
F = S.B²/(2µ)
où S est la section de l'aimant et µ est 4pi10^-7 et B, évidement le champ magnétique (en Tesla).
Ce qui est rassurant avec votre pistolet est que vous ne risquez pas de bléser personne.
Au revoir.

[invite52dd35ad]

Avant tout, merci pour la réponse !
Mais j'aimerais bien savoir comment est parachutée la formule ^^'

Et aussi, je peux me tromper dans le calcul, mais quand j'applique :

F = S.B²/2µ
F = d².B²/8µ = 0.045².1.35²/3,2*10^-6
F = 1150N
Diamètre de 45mm donc formule approximativement vraie sur 45mm.
E = F*l = 1150*0.045 = 50J

En France, pour l'airsoft, la limite légale est de 2J.
Donc a priori, 50J suffit amplement pour dégommer des playmobils ha ha

[LPFR]

Bonjour.
Faites attention de ne pas vous dégommer un œil.

La formule vient de l'énergie d'un volume dans lequel règne un champ B. Elle est V.B²/(2µ).
On la démontre en calculant l'énergie pour créer un champ uniforme dans une bobine avec la bonne géométrie.

Puis on dit que quand la distance entre deux objets magnétiques proches change, seul le volume entre les deux (et l'énergie) change. Comme le travail est F.d, il suffit de calculer F.

Mais cette formule est faite pour un aimant et/ou électroaimant et une masse de fer. Je pense qu'elle s'applique aussi à deux pôles identiques proches. Mais je dois dire que je ne suis pas certain. Je n'ai jamais vu de confirmation. Et j'ai encore quelques aspects dont je ne suis pas sur.

Si l'énergie est celle que vous avez calculée, un aimant des dimensions similaires partira avec une vitesse de 150 km/h, ce qui est sacrement dangereux. Et votre aimant risque de ne pas survivre. Les aimants n'aiment pas qu'on les cogne. Ils perdent leur magnétisation.

D'autre part, quel est l'intérêt d'utiliser des aimants à la place d'un ressort ? Avec un ressort on peut obtenir des vitesses plus importantes pour une même énergie, car il est moins massif.
Au revoir.

[A voir en vidéo sur Futura]