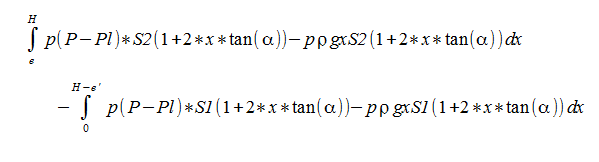Problème dans un cycle énergétique

[invite86cd2fbf]

Bonsoir,

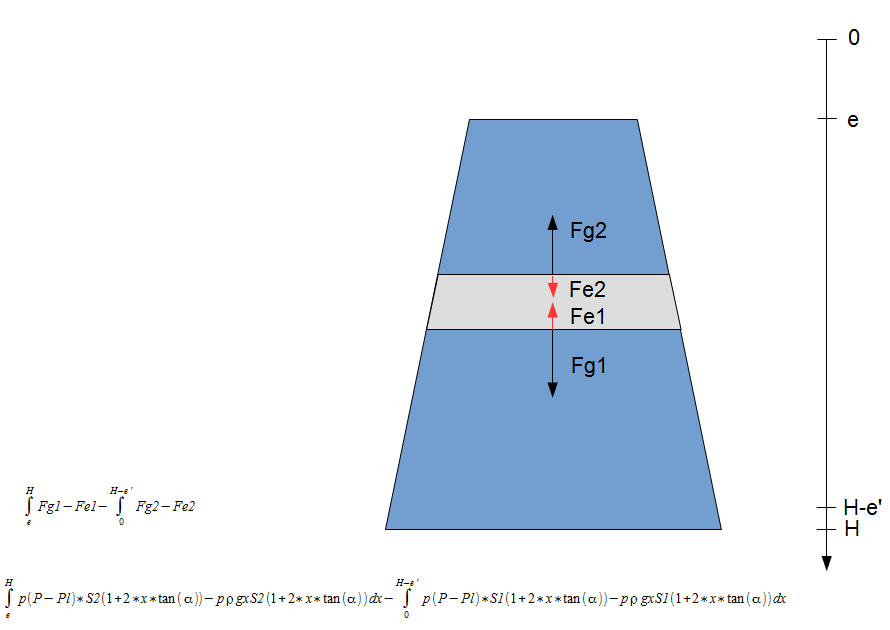
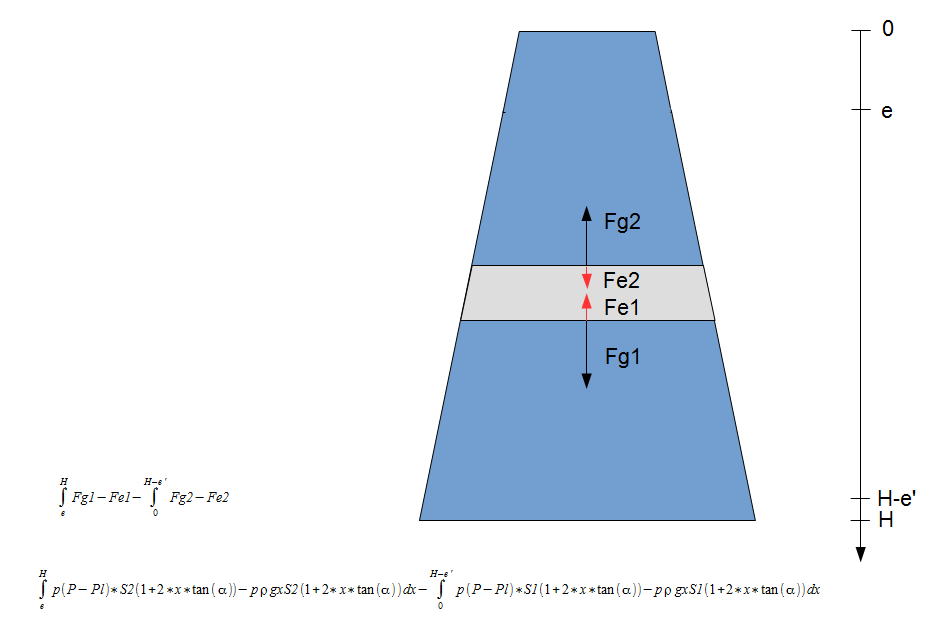
La manipulation se fait à la surface de la Terre. Un récipient R1 de forme trapézoïdale contient de l'eau à la pression atmosphérique. Un autre récipient R2 de forme également trapézoïdale contient de l'air à la pression atmosphérique. R2 comporte une petite cheminée très fine.

x1.png

On effectue le cycle suivant:

1/ On place R2 sur R1, cela consomme l'énergie pour soulever le poids du récipient R2
2/ Les parois de R1 (parois théoriques) bougent et englobent R2. Cela consomme l'énergie pour soulever les parois supplémentaires mais on a gagné en énergie potentielle donc on n'a rien perdu. Les dimensions de R2 font qu'il n'y a presque pas d'espace entre les parois de R1 et de R2 en haut et sur les côtés (pas les pentes). Sur les pentes on "supprime les parois de R2" (en fait on les place dans R2) et on met de joints pour assurer l'étanchéïté entre R1 et R2.

x1b.png

3/ On met de l'eau entre R1 et R2, cela consomme l'énergie pour monter de l'eau mais en quantité très faible (l'interstice doit permettre à l'eau de fournir la pression en dessous et permettre la circulation de l'eau)
4/ On ramène la pression à l'intérieur de R1 à 0.1 bar en utilisant la cheminée de R2, cela consomme peu d'énergie si les dimensions sont bien choisies, mais j'avoue que j'estime mal cette donnée.
5/ On déplace les surfaces S1 et S2 ainsi que les surfaces de côtés (pas les pentes car elle n'existent plus, c'est directement les surfaces de R1) ON EST A VOLUME CONSTANT POUR R2, la pression dans R2 est toujours la même. Cela fournit de l'énergie

x1hf.png


AN en arrondissant quelques valeurs:

H = 5 m
P = 1 bar
Pl = 0.1 bar
p = 1 m
S2 au départ = 1 m
α = 15 °
e = 0.2 m
g = 10 m/s²
ρ = 1000 kg/m3
e' est la nouvelle épaisseur pour donner le volume constant V. Le volume de départ est h*(S2-2*e*tan(α))*p = 0.178 m3. Donc e' vaut e'(S2'-2*e'*tan(α))=V=0.178 donc e'=0.05 m.

L'énergie fournit est d'environ 62000 J. On récupère aussi l'énergie du poids de R2 qui descend.


x1f.png

6/ On reconstitue la paroi de R2 pour refaire une forme fermée. On détache R2 de R1, cela ne consomme pratiquement rien. On peut changer la forme de R2 car il y a toujours la même pression à l'intérieur (volume identique). R1 a monté de e' soit un gain en énergie de : 1000*4.46*0.05*10 = 2232 J

7/ On remet sous pression atmosphérique R1, cela ne consomme pratiquement rien.

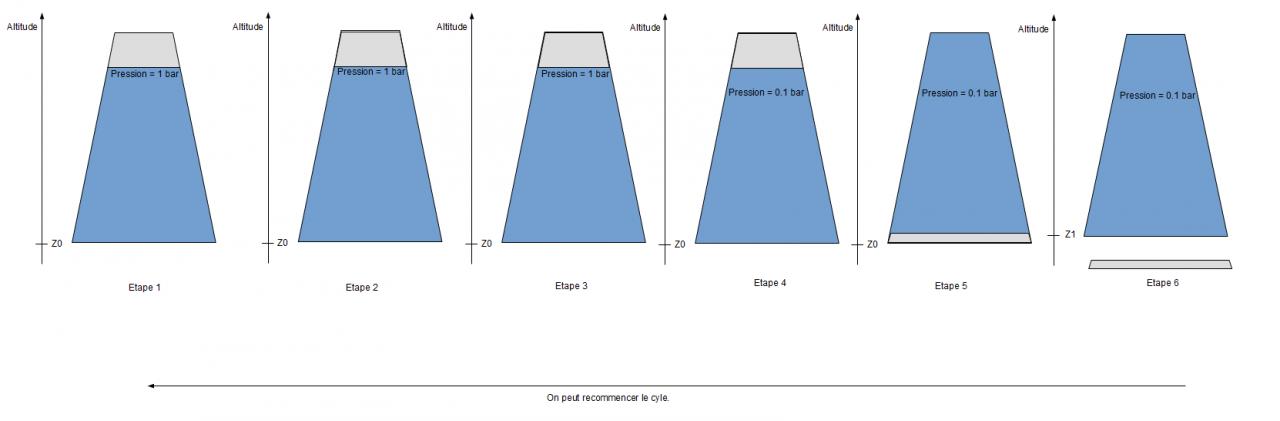
Les cycles de 1 à 6 :

x1g.jpg

Le cycle peut ainsi recommencer. Comme il y a conservation de l'énergie cela signifie que j'ai omis un détail important. J'ai considéré l'eau incompressible mais la différence de pression de 0.9 bar ne doit pas vraiment changer le volume de l'eau. Les parois sont théoriques peut être est ce là la source du problème. Ou alors il s'agit de la friction de l'eau mais là on pourrait aller doucement et les forces en jeu sont importantes quand même. Ou alors une erreur dans mon intégrale. Vous avez une idée de ce qui ne va pas dans le cycle ?

Voici la formule pour WxMaxima:

float(integrate(1*(100000-10000)*1*(1+2*x*tan(0.261))-1*1000*10*x*1*(1+2*x*tan(0.261 )),x,0.2,5)-integrate(1*(100000-10000)*0.892*(1+2*x*tan(0.261) )-1*1000*10*x*0.892*(1+2*x*tan(0 .261)),x,0,4.96));

A++ et merci d'avance pour vos réponses.
-----

[LPFR]

Bonjour.
Je suppose que votre engin est un d'innombrables "mobiles perpétuels" que l'on trouve partout.
Ils ne sont acceptés dans ce forum.
Mais on peut, comme exercice, démontrer l'erreur dans le raisonnement.

Le problème est que votre explication n'est pas claire. Je n'ai rien compris au début de la manip.

Ce n'est pas la peine d'utiliser des variables comme R1 et R2 pour décrire la manip.
(à chaque coup il faut revenir au début pour revoir laquelle est laquelle).

Bref, si vous ne décrivez pas votre manip clairement, je pense que cette discussion sera fermée.
Au revoir.

[invite86cd2fbf]

Bonjour,

Je suis désolé si vous n'avez pas compris. J'ai sans doute omis des points importants. Je sais que les mobiles perpétuels ne sont pas acceptés mais j'essai de comprendre d'où vient l'erreur, j'ai donné des explications, j'ai fait des dessins et j'ai essayer d'intégrer la somme des travaux. Et oui, à titre d'exercice ce serait sympa de me montrer où est l'erreur car je ne trouve pas tout seul.

Au début de la manip:

Pour faire simple: R1 = grand récipient, et R2 petit récipient.

Un grand récipient fermé contient de l'eau, il est fixé à une certaine hauteur Z0 par un élément externe, il y a à l'intérieur la pression de 1 bar mais très peu de gaz (volume). Un petit récipient fermé contient du gaz à la pression de 1 bar. Ils ont tous les deux une forme trapézoïdale (voir dessins, dites moi s'ils ne sont pas assez clairs ?). Je prends le petit récipient et je le monte sur le grand, ensuite j'étends les parois du grand récipient pour englober le petit. Le petit récipient est toujours fermé. Il y a très peu de gaz entre les parois du grand récipient et du petit, on ajoute de l'eau entre les deux récipients, en très faible quantité car il y a peu d'espace entre les deux parois. On retire la pression pour atteindre 0.1 bar dans le grand récipient à l'aide de la petite cheminée du petit récipient. On "supprime" les surfaces des pentes du petit récipient en mettant des joints, maintenant le petit récipient n'a plus que les surfaces du haut et du bas ainsi que sur les côtés. Voilà la manip est prête. On descend les surfaces S1, S2 ainsi que les surfaces des côtés pour avoir le volume du petit récipient constant, cela jusqu'en bas. Les surfaces des côtés ne travaillent pas car la force de pression est perpendiculaire au mouvement. Seules les surfaces S1 et S2 travaillent, j'ai donc calculer la somme de l'énergie que cela demande avec les intégrales. Une fois en bas, je remets les parois du petit récipient et je le détache du grand. L'eau est montée et a fournit un travail aussi.

J'espère que c'est plus facile à comprendre comme cela.

Merci d'avance pour votre aide

[LPFR]

Bonjour.
Merci. Oui. C'est beaucoup plus clair maintenant.
Mais pas le raisonnement.

Pour descendre le petit récipient il vous fournir un travail contre la poussée d'Archimède

Le rôle des parois en trapèze n'est pas clair. Il est la pour essayer de compliquer les raisonnements.

Et pour compliquer les choses. Car pour changer la forme du volume du petit récipient sans changer le volume, ni faire du travail, ce n'est pas immédiat. C'est parfaitement possible mais il faut calculer le déplacement des deux surfaces haut et bas et le travail fait par les forces de pression.
Au revoir.

[A voir en vidéo sur Futura]

[invite86cd2fbf]

Oui, pour descendre le petit récipient il y a des forces de pression de la part de l'eau et des forces de pression de la part du gaz. L'eau pousse sur S2 vers le haut et pousse sur S1 vers le bas, c'est Fe1 et Fe2. Le gaz pousse S2 vers le bas et S1 vers le haut, c'est Fg1 et Fg2. Les parois latérales n'agissent pas je pense.

Pour les pentes du petit récipient, je les enlève, le gaz du petit récipient est donc en contact avec les pentes du grand récipient, mais le grand récipient est fixe. Il y a des joints pour assurer l'étanchéité.

Pour descendre le petit récipient, qui n'est plus vraiment un récipient, il est en fait constitué de 4 surfaces S1, S2, les parois verticales car les deux parois des pentes sont assurées par le grand récipient. Du coup, j'ai intégré le travail des force dues au gaz et dues à l'eau sur S1 et S2 uniquement. C'est peut être là mon erreur.

[LPFR]

Re.
Vous ne pouvez pas négliger les forces sur les parois latérales inclinées. Leurs composantes horizontales se compensent avec celles sur les autres parois. Mais la composante verticale joue et ne se compense pas.
Si les parois inclinées sont immobiles (c'est dur à faire en pratique, mais c'est une expérience imaginaire), alors, effectivement, seules les forces sur les parois horizontales sont à considérer.

Donc, à priori, vos intégrales semblent correctes. Mais il faut remplacer les pressions en fonction la position.
Pour la pression hydrostatique, seule la profondeur compte. Mais pour la pression du gaz, c'est le volume entre les surfaces qui compte.

Conseil: quand vous avez un problème de ce type il ne faut pas faire le dessin à une des extrémités du parcours, mais dans une position intermédiaire quelconque.

Pour l'instant, ces phases de la manip consomment du travail. Et ce travail sera récupéré quand on enlève le petit récipient du bas du grand. (Vous pouvez l'imaginer en tirant le petit réservoir sur le côté comme si c'était un tiroir. Après avoir rétabli les parois inclinées, bien sur).
A+

[invite86cd2fbf]

Re,

Oui, les parois inclinées sont immobiles, il n'y a que le grand récipient, effectivement, difficile à faire en pratique.

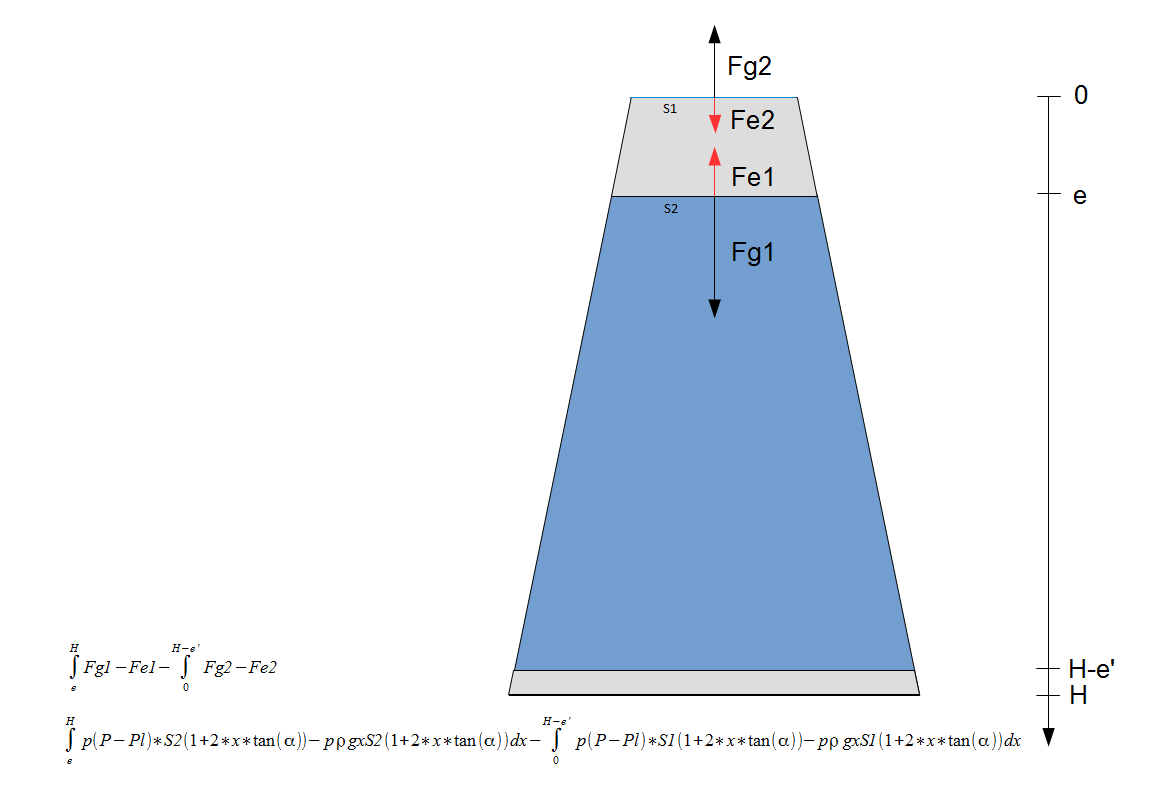
En ce qui concerne la pression en fonction de la position, comme le volume du petit récipient est constant, il y a toujours la même pression de 1 bar à l'intérieur, non ? Pour la pression de l'eau, j'ai pris avec x la position de profondeur, ce n'est pas comme cela qu'il faut faire ? Et comme le volume du petit récipient est constant la pression qui provient du gaz dans le grand récipient (0.1 bar pour l'exemple) doit être constante, non ?

Le calcul avec les intégrales indique une énergie fournie par la descente puisque j'ai compter en positif la force que fournit la pression sur S2, c'est peut être là mon erreur ?

Voici l'équation pour WxMaxima si vous voulez bien vérifier

float(integrate(1*(100000-10000)*1*(1+2*x*tan(0.261))-1*1000*10*x*1*(1+2*x*tan(0.261 )),x,0.2,5)-integrate(1*(100000-10000)*0.892*(1+2*x*tan(0.261) )-1*1000*10*x*0.892*(1+2*x*tan(0 .261)),x,0,4.95));

[invite86cd2fbf]

Désolé, petite erreur sur le dessin précédent:

[LPFR]

Re.
Je ne comprends pas les valeurs numériques que vous avez mis pour
p, P, Pl,
Ce qui m'empêche de deviner ce qu'il représentent.
Et l'intégrale peut se faire analytiquement.
A+

[invite86cd2fbf]

Re,

p est la profondeur
P est la pression du gaz à l'intérieur du petit récipient, constante 1 bar
Pl est la pression qu'on a après avoir mis l'eau (on retire de la pression essentiellement à l'eau car il y a peu de volume de gaz), elle vaut 0.1 bar

Je vous donne dès que j'ai trouvé l'intégrale analytique.

[invite86cd2fbf]

Voilà j'ai trouvé les intégrales analytiques, j'ai fait un changement de variable avec A et B pour simplifier les calculs. J'ai vérifier avec l'application numérique et ça donne le même résultat qu'avec mon exemple.

x1m.png

ou voici l'intégrale complète:

integrate(p*(P-Pl)*S2*(1+2*x*tan(\alpha))-p*\rho*g*S2*x*(1+2*x*tan(\alph a)),x)-integrate(p*(P-Pl)*S2*(1-2*e*tan(\alpha))*(1+2*x*tan(\a lpha))-p*\rho*g*S2*x*(1-2*e*tan(\alpha))*(1+2*x*tan(\a lpha)),x);

et:

x1n.png

[LPFR]

Re.
Ce que vous faites est incompréhensible.
Qu'est que fait la variable 'p' profondeur, constante, alors que vous intégrez sur la profondeur 'x' ?

Commencez par faire le calcul avec les parois verticales (alpha = 0) et regardez ce que vous obtenez.

L'intégrale est analytique. Faites-la à la main et vous comprendrez ce que vous faites.

Et que conquérez-vous avec le résultat une fois correctement calculé ?
Qu'il faut fournir du travail pour faire descendre le gaz ? Ça on le savait avant.
Et que faites-vous du travail pour "faire le vide" ?
Et alors, de quel cycle parliez-vous ? Vous ne calculez pas le travail pour revenir aux conditions initiales. Donc, je ne vois pas quel pourrait être le problème, avant de calculer le travail sur un cycle complet.


Franchement, j'ai de moins en moins envie de détricoter vos calculs. Car je ne vois même pas "l'astuce" de votre mobile perpétuel (ce qui le ferait passer, à première vue, par un mobile perpétuel. Il y en a de très amusants. Mais le vôtre n'est même pas un projet de "mobile perpétuel".
A+

[invite86cd2fbf]

Re,

J'intègre sur x, avec x est la hauteur, la profondeur est constante dans l'application numérique, elle vaut 1 m. Les surfaces S1 et S2 descendent, je dois intégrer sur la hauteur, non ?

Je vais faire les calculs à la main et essayer de trouver mon erreur. Oui, je vais trouver une consommation d'énergie, même si on connait le résultat, j'apprends.

Il est vrai aussi qu'il faut du travail pour réduire la pression à 0.1 bar dans le grand récipient mais théoriquement, si le volume de gaz est très faible l'énergie ne doit pas être énorme, la différence de pression est faible et l'eau ne doit pas se décomprimer beaucoup, ici j'ai 62000 J en trop, je ne pense pas que ce soit cela.

Merci pour votre aide et désolé de vous déranger

[invite86cd2fbf]

Je viens de vous comprendre, pour vous la profondeur c'est la profondeur dans l'eau, pour moi c'est la hauteur. Ce que j'ai appelé la profondeur de l'objet c'est la dimension qui traverse l'écran (z en math). La profondeur est bien constante et vaut 1 mètre. Maintenant, j'intègre bien sur la hauteur, donc votre profondeur mais ça n'a rien à voir avec p (petit p). Comme quoi les mots sont importants et leur contexte encore plus !

Comme vous me l'avez demandé j'ai remplacé dans l'équation de l'application numérique avec une angle , du coup ce n'est plus un trapèze, mais un rectangle de 4.8 m de haut et e vaut 0.2 m. Mon calcul me donne -9600 J maintenant il faut bien fournir de l'énergie. Et cela correspond à la hauteur de l'eau qui a monté de 0.2 m soit soit 9600 J.

Vous parliez d'astuce tout à l'heure, ici l'astuce serait de descendre un volume de gaz dans l'eau, avec une eau qui n'est plus en présence de gaz sous pression mais uniquement la pression de l'eau. Le petit volume descend avec plus de pression venant de P mais perd en contrepartie la pression de l'eau. Mais la pression de l'eau n'est plus dépendante de la pression du gaz. Tant qu'on est inférieur à 10 m cela me sembler une bonne idée. Bon on est d'accord c'est juste un jeu. Je sais pas si c'est clair pour vous ?

J'espère que vous n'êtes pas fâché et que vous voudrai bien m'aider encore un peu

Bonne soirée

[sitalgo]

B'jour,

Sérieux problème avec les forces qui agissent sur les plaques.
Gardons le système rectangulaire, c'est plus simple et ça ne change rien au principe.
Comment fais-tu pour que la pression du gaz et donc l'écartement des plaques indépendantes restent constants.
Parce que quand on passe l'eau de 1 à 0,1 bars, il y a fort à parier que le volume du gaz va être multiplié par 10.
Ça devrait répondre à ton questionnement.

[invite86cd2fbf]

@Sitalgo: vous parlez bien des surfaces S1 et S2 ? Si oui, imaginez qu'elles sont contrôlées chacune par un vérin hydraulique (si vous voulez pour l'aspect technologique), je peux les asservir en position avec des vérins il me semble. Maintenant les forces sont ce qu'elles sont et si je bouge les vérins je fournis une énergie étant la force multipliée par la distance (au rendement près bien entendu). Ce n'est pas possible ainsi ?

Ensuite quelque chose d'important est que le petit volume est constant. Le grand volume est clos et constant aussi.

Gardons le système rectangulaire, c'est plus simple et ça ne change rien au principe.

Je n'ai aucun problème de calcul avec le petit volume s'il est rectangulaire et je souhaite comprendre pour un trapèze si c'est possible.

[invite86cd2fbf]

@LPFR: pour répondre à votre question sur le cycle complet, je reprends l'image fournit au premier message:



Sur un plan théorique:

Etape1: on place le petit volume sur le grand, cela consomme de l'énergie pour monter le volume mais on gagne en énergie potentielle

Etape2: On grandit les parois du grand récipient pour envelopper le petit, cela consomme de l'énergie mais on gagne la même chose en énergie potentielle

Etape3: On ajoute de l'eau entre le récipient 1 et le récipient, si l'épaisseur entre R1 et R2 est de i = 2 mm, on consomme avec S la surface totale entre le petit récipient et le grand et H la hauteur. Ce qui donne dans l'application numérique 276 J si on considère qu'on monte du bas du grand récipient

Etape4: On ramène la pression à 0.1 bar. C'est difficile à calculer sur le plan pratique mais en théorie cela doit être faisable. On peut par exemple ne considérer que le volume de gaz de la cheminée pour baisser la pression. Si la cheminée fait 1 mm de diamètre et 20 mm de hauteur cela donne un volume de gaz à ce qui fortement limiter la perte d'énergie. Il y a aussi l'eau qui prend plus de volume. J'aurai bien besoin d'un coup de main pour un calcul précis même si pour moi la consommation d'énergie est très faible en théorie comparée à plusieurs dizaines de milliers de Joules. C'est peut être là mon erreur.

Etape5: On déplace les surfaces S1, S2 et les parois verticales. Il n'y a pas de paroi pentue car c'est le grand récipient (fixe) qui assure cela. Voir les intégrales pour les énergies. Les parois qui descendent fournissent très peu d'énergie, c'est l'énergie qu'on avait fournit à l'étape 1. J'ai un doute ici également.

Etape6: On reforme les parois des pentes du petit récipient pour le rendre clos. Et on le détache du grand récipient. L'eau a monté de 0.05 m soit un gain d'énergie. On reforme également le petit récipient comme il était au départ, cela ne consomme rien puisqu'il y a toujours 1 bar à l'intérieur. Le gain en énergie est de 5400 J car on monte de 0.05 m

Etape7 (pas de dessin): On remet la pression de 1 bar dans le grand récipient. La consommation d'énergie ne doit pas être très importante et s'il elle provient de la pression atmosphérique, elle ne demande pas d'énergie (c'est juste pour simplifier les calculs).

On recommence le cycle car on a les mêmes conditions qu'à l'étape 1.

[sitalgo]

Si oui, imaginez qu'elles sont contrôlées chacune par un vérin hydraulique (si vous voulez pour l'aspect technologique), je peux les asservir en position avec des vérins il me semble.

Pas besoin de vérin, une barre d'écartement suffit.
Maintenant quel est l'équilibre d'une plaque ?

[LPFR]

Bonjour.
Regardez la zone bleue entre les étapes 5 et 6 du dessin du post #17: Le volume d'eau est plus haut d'une distance égale à l'épaisseur de petit récipient.
Vous avez dépensé de l'énergie pour descendre le petit récipient, et cette énergie s'est transformée en énergie potentielle de la masse d'eau qui a augmenté de hauteur.

Vous avez utilisé un processus extrêmement tarabiscoté pour ne rien gagner ni perdre, si on ignore toutes les manips inutiles que vous avez ajoutées et qui ne servent qu'à rendre l'ensemble du processus plus opaque et vous entrainer à faire des erreurs dans le calcul.
Au revoir.

[invite86cd2fbf]

Bonjour LPFR,

Merci de m'aider. Oui, j'ai certainement dû faire une erreur de calcul. Effectivement, entre les étapes 5 et 6 le volume d'eau est plus haut et il y a un gain d'énergie de 5584 J. Ce que je ne comprends pas c'est que mes intégrales me donne une travail positif (je gagne de l'énergie) bon à la limite je pourrai dire que c'est une erreur de signe que je ne vois pas. Mais le résultat n'est pas en correspondance, je trouve 62000 J, on en est loin. Je ne trouve pas mon erreur. Malgré tout, j'ai fait le calcul en mettant et je trouve bien 9600 J avec les intégrales et cela correspond au calcul direct que l'on peut faire. Si vous voyez l'erreur ?

A++

[LPFR]

Re.
Non, je ne vois pas l'erreur et je n'ai pas envie de plonger dans vos équations. Commencez par faire un exemple simplifié, sans les complications absurdes que vous avez ajoutées. Parois verticales, surfaces égales et tenues à distance constante. Quand vous aurez trouvé votre erreur vous pourrez le compliquer.

Pour ce qui est du signe, si vous considérez les forces positives vers le bas quand les surfaces descendent, vous êtes en train de calculer le travail faut pas ces forces, c'est à dire le travail que vous avez été obligé de fournir et que le système a reçu. Il est évidement positif dans cette phase.

Au lieu d'appliquer des formules, il faut toujours savoir ce que l'on calcule. Surtout pour le travail. Il faut savoir si on calcule le travail fourni ou le travail reçu.
A+

[invite86cd2fbf]

Re,

D'accord. Voici un exemple plus simple, il s'agit de descendre un volume rectangulaire. Les parois sur les côtés du petit volume n'existent plus, et il y a des joints.

car1.png


Application numérique:

S = 1 m
H = 5 m
e = 0.2 m
p = 1 m

P = 1 bar
Pl = 0.1 bar

Voici l'équation WxMaxima si vous voulez vérifier:

float(integrate(1*(100000-10000)*1*(1+2*x*tan(0))-1*1000*10*x*1*(1+2*x*tan(0)),x ,0.2,5)-integrate(1*(100000-10000)*1*(1+2*x*tan(0))-1*1000*10*x*1*(1+2*x*tan(0)),x ,0,4.8));

x1e.png

On trouve 9600J

Maintenant, si on vérifie avec les formules, on a monté un volume d'eau de sur 0.2 m soit une énergie nécessaire de 9600 J

Cela correspond bien et montre que les intégrales semblent corrects à part peut être l'élément en tan ou j'ai peut être fait une erreur ?


Pour reprendre mon cas avec les trapèzes:

J'ai quand même essayé d'estimer théoriquement l'énergie nécessaire pour abaisser la pression pour le volume concerné. En abaissant la pression, l'eau va "gonfler" par conséquent, au lieu de rajouter de l'eau à l'étape 3, je peux simplement prévoir le gonflement de l'eau pour ajuster, à la fin il n'y a donc plus que de l'eau (théoriquement). Si j'ai pas d'erreur de calcul la densité de l'eau à 1 bar est de 0.9999993709, à 0.1 bar elle est de 0.99995663 soit une différence de densité de 0.0000427, comme le volume est de presque cela donne un volume en plus de 0.4 litre. Si j'ai bien compris, pour trouver l'énergie nécessaire à abaisser la pression, il faut faire l'intégrale de PdV. Ici le volume est de 0.0004 M^3 et la pression varie de 100000 Pa à 10000 Pa. Ce qui donne 42 J environ. Il y a certainement d'autres paramètres à tenir en compte comme la température mais peut que cela donne une idée de l'énergie nécessaire à faire le vide, juste pour comparer avec les 62000 J en trop. Donc, c'est certainement une erreur dans le tan ?

Merci d'avance pour votre aide.

[LPFR]

Re.
Arrêtez de vous prendre la tête avec l'abaissement de pression. Faites simplement toute la manip dans le vide (ou à la pression de vapeur de l'eau à la température de travail).
A+

[invite86cd2fbf]

Re,

C'est à dire ? Dans le vide pour l'eau mais je peux garder la pression P dans le petit volume ?

a+

[invite86cd2fbf]

Ouiiiiiiiiiiii ! je viens de comprendre, effectivement, cela évite ce calcul. Et cela ne change pas les résultats pour le modèle simplifié. Pour le modèle trapézoïdal, il suffit de mettre Pf à 2000 Pa par exemple et l'énergie fournit est encore plus grande.

a+

[invite86cd2fbf]

Ce n'est pas une erreur sur le terme ?



P = Pression dans le petit récipient
Pl = Pression de l'eau (pression que le gaz ajoute à l'eau), peut être limitée à la pression de vapeur
S2 = Surface du bas
S1 = Surface du haut
p = profondeur (pas l'altitude) de l'objet (axe qui traverse l'écran)
g = accélération de la gravité
= masse volumique de l'eau
x = terme de l'intégration (hauteur ou profondeur dans l'eau)
H = Hauteur totale
e = hauteur du petit récipient au départ (en haut)
e' = hauteur du petit récipient à la fin (en bas)
= angle du trapèze

Ou alors c'est une erreur conceptuelle, quelque chose dans une étape qui n'est pas possible. Car en abaissant le petit récipient, en utilisant les parois fixes du grand récipient pour les pentes, cela fait travailler la pression P sur une surface supplémentaire qui vaut (S2-S1), et S2-S1>0 pendant tout le déplacement, bien entendu l'eau fait travailler dans le sens contraire mais la pression de l'eau n'est dépendante que la profondeur (plus un terme fixe qui peut être très réduit à la pression de vapeur) mais comme on est à moins de 10 mètres, la pression P travaille plus que la pression de l'eau. Quelqu'un peut m'expliquer ce point ?

a+

[invite86cd2fbf]

Bonjour,

Pour moi l'énergie provient du gaz contenu dans le petit volume. Car S2 > S1 tout le temps de la descente du petit volume. Le gaz accélère la surface S2 mais S1 ne peut pas accélérer autant le gaz car elle est toujours plus petite. Si on recommence le cycle plusieurs fois (et on peut il suffit de reformer le petit volume ce qui ne consomme en théorie pas d'énergie), la température (et donc la pression) du petit volume va finir par être à 0. Certe la température à l'extérieur du petit volume est augmentée mais moins car la pression est moindre. Qu'en pensez vous ?

Merci d'avance pour votre aide

A++

[LPFR]

Bonjour.
Je pense qu'il est temps de fermer cette discussion sur un prétendu "mobile perpétuel".

Je vous ai déjà expliqué, y compris par MP, pourquoi ce n'est pas un "mobile perpétuel".
Mes explications ne vous satisfont pas. Tant pis.
En tour cas j'arrête.
Au revoir.