calcul de loxodromie...
Bonjour,
Beaucoup de sujets sur cette loxodromie, mais assez peu de calculs (ou alors j'ai mal regardé)
Voici mon petit problème :
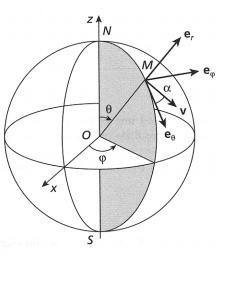
On considère la Terre sphérique de rayon R. un bateau navigue avec une vitesse de module v0 contant, et dont la direction fait en permanence un angle α constant avec le méridien du lieu. On désigne par ϴ0 et ϕ0 les valeurs de ϴ et ϕ à t=0.
1. Exprimer le vecteur vitesse du bateau situé en M dans la base locale sphérique.
2. En déduire les expressions de ϴ et ϕ’.
3. En intégrant l’expression de ϕ’ déterminée en 2, montrer que ϴ et ϕ sont reliés par l’équation suivante (trajectoire appelée loxodromie) :
C'est surtout cette dernière expression que je n'arrive pas à trouver... et pour laquelle je vous demande de l'aide...
Voilà jusqu'où j'arrive :
1) V du bateau dans le repère sphérique "classique"
2) En dérivant le vecteur position OM dans le repère sphérique, on obtient :
et donc en identifiant j'obtiens =>
le problème est donc bien d'intégrer ces expressions, mais avoir
merci de votre aide !
PS : je me demande si on calcule de la même manière l'orthodromie....(question subsidiaire...)
-----
