Oscillateur sinusoïdal

[Cajanec]

Bonjour,

J'ai un petit souci de compréhension pour l'exercice ci-dessous (la question 1 uniquement).

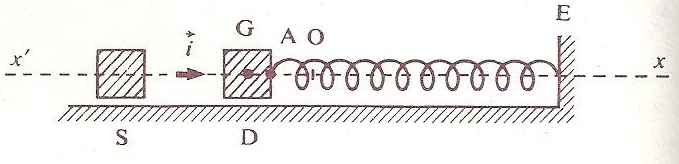
Une extrémité d'un ressort d'axe horizontal x'x, de raideur k et de masse négligeable, est fixée à une butée fixe E. L'autre extrémité est solidaire d'un palet D de masse M ; D peut se déplacer sur une table horizontale à coussin d'air d'un mouvement de translation rectiligne suivant un axe (x'x, )



1) Le palet est écarté de sa position d'équilibre, vers la droite, d'une distance a. On le lâche sans vitesse initiale. Montrer que le système constitue un oscillateur sinusoïdal dont on donnera l'équation horaire du mouvement.

Classiquement on trouve que l'équation différentielle du mouvement est :

Je ne récrit pas cette démonstration ici, car elle ne me pose pas de problème.
Ce qui me perturbe beaucoup c'est que, dans la correction proposée pour cette question, il est écrit que PUISQUE l'équation différentielle du mouvement est de cette forme (formule ci-dessus) ALORS le mouvement est oscillatoire sinusoïdal.
Ça me semble un peu rapide, pour moi ce n'est pas une vraie démonstration.

La solution d'une telle équation différentielle est-elle toujours une solution sinusoïdale ?
Si oui, comment le démontrer ?

Merci par avance.
-----

[ulyss]

Bonjour,

C'est plutôt une question de mathématiques, çà... il faut regarder la démonstration de la résolution des équations différentielles du second ordre.
Voilà un lien pour une démo complète :
http://www.math.u-psud.fr/~perrin/CA...iff07.K/m1.pdf

Sinon ici on veut résoudre : d²x/dt² + K/m * x = 0
L'équation caractéristique associée est x² + K/m * x = 0
de solution w = i * racine (K/m) (i racine imaginaire de -1)
D'où la solution : x(t) = A cos (wt ) + B sin (wt)
qui s'écrit usuellement en physique : x(t) = A cos (wt + phi) ou x(t) = A sin(wt + phi) au choix
avec A et phi à déterminer en fonction des conditions aux limites (initiales en générales)

Au revoir

[stefjm]

Le lien fonctionnel.

[ulyss]

Je me suis amusé à refaire cette démo pour ton cas :

Bon en gros la réponse consiste à considérer l'ensemble S des fonctions solutions de y" + w2 y = 0
On sait que c'est un espace vectoriel.
On connaît deux solutions évidentes : f1(t) = cos(wt) et f2(t) = sin(wt)
Ces deux fonctions solutions sont clairement linéairement indépendantes, donc il suffit de démontrer que S est de dimension 2 et le tour est joué!
(car si c'est le cas toute solution s'écrit comme combinaison linéaire de deux fctions sinusoïdales de même fréquence, et cela donne évidemment une fonction sinusoïdale)

Pour cela on raisonne ainsi : soit f solution quelquonque, à t fixé on cherche deux coefficients X(t) et Y(t) (ils dépendent a priori de t) tels que l'on ait:
f(t) = X(t) f1(t) + Y(t) f2(t) (a)
f'(t) = X(t) f1'(t) + Y(t) f2'(t) (b)

(à t fixé, X et Y sont les "inconnues" d'un système à 2 équations)

Le but est de montrer que X(t) et Y(t) existent pour tout t et qu'ils ne dépendent pas de t...

Existence de X(t) et Y(t) : on considère le déterminant du système soit:
| f1(t) f2(t)|
| f1'(t) f2'(t)|
qui s'appelle le "wronskien" W(t) de l'equa diff, on le calcule : il n'est pas nul (il vaut w ici)
X et Y existent donc.

"Unicité" : démontrons que X(t) et Y(t) ne dépendent pas de t. On va chercher à montrer que les dérivées de X et Y sont nulles.
Déjà X(t) et Y(t) sont dérivables (cf formule de Cramer de résolution du syst : X et Y sont des sommes et produits de f1 ; f1' ; f2; f2' tous dérivables avec une division par W(t) non nul)
Il ne reste plus qu'à montrer que X'(t) = 0 et Y'(t) = 0

Déjà par dérivation de (a) on a : f'(t) = X'(t) f1(t) + Y'(t) f2(t) + X(t) f1'(t) + Y(t) f2'(t)
Avec (b) on en déduit : X'(t) f1(t) + Y'(t) f2(t) = 0
on a alors aussi d'après (b) : f"(t) = X'(t) f1'(t) + Y'(t)f2'(t) + X(t) f1"(t) + Y(t)f2"(t)
Comme f , f1 et f2 sont solutions de y" + w2 y = 0 on remplace f" par -w2 f(t) dans cette expression, de même pour f1" et f2" et grâce à (a), tout cela s'annule et finalement on en déduit :
X'(t)f1'(t) + Y'(t)f2'(t) = 0
on a déjà X'(t) f1(t) + Y'(t) f2(t) = 0
Donc X'(t) et Y'(t) sont encore solutions d'un système dont le déterminant est encore le wronskien W qui est non nul, mais cette fois le second membre du système est nul. Et donc X'(t) = 0 et Y'(t) = 0 pour tout t.
CQFD

[A voir en vidéo sur Futura]

[Cajanec]

Ah, mes lacunes en mathématiques...
Merci à vous deux !