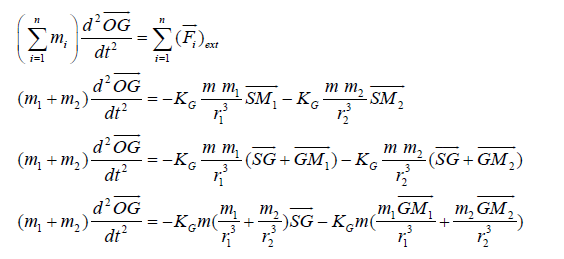Centre de masse et forces extérieurs, exemple : sys. solaire

[GaMeR-HAK]

Bonjour tout le monde j'éspère que vous allez bien

Lorsque je révisais la mécanique, je suis tombé sur une annexe expliquant l'erreur que se produit lorsqu'on utilise les propriétés du centre de masse dans
des cas bien précis.

Prenons l'exemple du système solaire ou nous allons étudier le soleil, la terre et la lune. La terre avec sa lune (la lune) looool, constitue le système en question, tandis que la force gravitationnelle du soleil représente la résultante des forces extérieurs appliquées au système.
Voici une image : meca.PNG

Terre (masse m1) Lune (m2) Soleil (m)
Les forces exercées par le Soleil seront considérées comme extérieures au système Terre Lune.
Si on voudrais simplifier le calcul, on pourrais se contenter d'étudier le mouvement du centre de masse du système Terre Lune en attribuant à celui ci la
masse (m1+m2)
on écrit donc :

meca 2.PNG

Mais le problème ici c'est que cette équation est FAUSSE !

commencant par le deuxième principe de la dynamique :
meca 3.PNG

Làààà je me coince !!
je n'ai pas compris comment a t-on fait pour passer de l'avant dernière ligne à la dernière ??

je vous donne la suite de l'annexe :
meca 4.PNG

Je vous en pris, aidez moi à comprendre cette manipulation !

Merci d'avance
-----

[LPFR]

Bonjour.
Pour le passage entre « l'avant dernière ligne à la dernière » je ne vois pas le problème. C’est un simple regroupement. Il suffit de développer les parenthèses pou constater qu’il n’y a pas d’astuce.

Pour ce qui est la démonstration dans son ensemble, je me demande dans quelle poubelle l’avez-vous trouvée. Son seul « mérite » est de compliquer l’écriture pour cacher la force interne au système (entre la Terre et la Lune) qui s’annulent tout simplement parce que sont des action et réaction (troisième loi de Newton).
Au revoir.

[Dynamix]

Salut

Si on voudrais simplifier le calcul, on pourrais se contenter d'étudier le mouvement du centre de masse du système Terre Lune en attribuant à celui ci la
masse (m1+m2)

Pour l'' équilibre des forces gravitationnelles le centre de masse ne joue aucun rôle .
C' est le centre de gravité qui compte .
Dans un tel champs ces deux points ne sont pas confondus et ta démonstration le prouve .

[GaMeR-HAK]

Merci monsieur Dynamix, mais la démonstration n'est pas la miènne , c'est juste copiée d'un cours
le problème ici est mathématique, je n'ai pas compris comment a t-on passé de l'avant dernière ligne à la dernière dans cette image ci-dessous illustrant la démarche :


SVP pourriez-vous m'aider

[A voir en vidéo sur Futura]

[Dynamix]

LPFR l' a expliqué :
1_développer ce qui donne :
-KG[(m.m1/r1³)SG+(m.m1/r1³)GM1+(m.m2/r2³)SG+(m.m2/r2³)GM2]
2_regrouper les termes de même couleur

Pour préciser un pau le sens de mon post précédent :

Mais le problème ici c'est que cette équation est FAUSSE !

Oui , le calcul de la force de gravité est faux du fait que l' accélération gravitationnelle n' est pas la même pour la terre et pour la lune .
Donc elle n' est pas égale au produit de la masse par l' accélération au point G

Si on voudrais simplifier le calcul, on pourrais se contenter d'étudier le mouvement du centre de masse du système Terre Lune en attribuant à celui ci la
masse (m1+m2)

On doit le faire du point de vue inertie .
Mais en donnant à la force gravitationnelle la bonne valeur et en considérant que son moment n' est pas nul au centre de masse .