Salut !
J'ai un problème avec cet exercice. En effet, je trouve une valeur de, pour tout t.
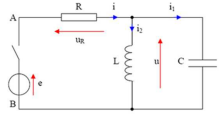
Voici le circuit :
Je trouve l'équation différentielle :
Et pour les conditions initiales :
Pareil que mon sujet précédent (je poste beaucoup aujourd'hui), je ne vois pas ou est-ce que j'ai pu faire une erreur...
Merci d'avance,
Dernière modification par JPL ; 17/01/2015 à 19h59.
Salut !
Je trouve pas la même équation différentielle que toi, tu es sûr de ton coup ?
Bonjour.
Votre deuxième condition initiale di/dt = 0 est fausse.
La pente initiale de ‘i’ est la même que pour la charge du condensateur sans la self.
Au revoir.
OK, je m'incline, je viens de voir !Envoyé par benjy_star
Oh, une petite précision (bien sur j'oublie un détail important) : RC = L/R
Mais je suis plutôt sur de mon équation différentielle. On a Uc aux bornes du condensateur, donc i1 = C*dUc/dt.
On a Ul aux bornes du self qui est de L*di2/Dt, mais on voit également que Uc = Ul.
Donc on a i = i2 + C*du/dt, et donc Ur aux bornes de la résistance R*C*du/dt + Ri2.
Loi des mailles :
0 = E - RC*dUc/dt - Ri - L*di/dt, donc L*di/dt + RC*dUc/dt + Ri = E.
On dérive Uc et dUc/dt = L*d²i/dt² et on injecte :
RLC*d²i/dt² + L*di/dt + Ri = E et en divisant le tout par RLC on trouve :
d²i/dt² + 1/RC*di/dt + 1/LC*i = E/RLC !
Pourtant, en t=0, le condensateur se comporte comme un générateur de tension, et vu qu'il n'est pas chargé, il est équivalant à un fil.
La tension dans un fil est nulle, donc Uc(0)=0.
Mais Uc = L*di/dt, d'ou di/dt(0) = 0. Non ?
D'une autre manière, aux bornes de la self en t=0, on a L*di/dt. On fait donc une loi des mailles puisqu'on connait la valeur de i et 0 = E - Ri - L*di/dt.
Ri = E, donc L*di/dt = 0 !
Ça a plutôt l'air de coller avec les valeurs de i en t=0 et en régime DC. Dans les deux cas, i=E/R.
Re.
Vous mélangez i, i2 et i1.
A+
Ah oui, effectivement.
Mais du coup je n'ai aucune idée de comment calculer di/dt(0)...
Re.
(10 caractères inutiles)A+
Ce qui m'intéresse ce n'est pas de résoudre un exercice, à la limite si celui-là reste sans solution, tant pis. Ce que je veux savoir moi, c'est le raisonnement derrière, comment on trouve les conditions initiales d'un circuit d'un second ordre.
La j'ai le droit à un résultat parachuté sans aucune explication. Je veux bien admettre que
Bonsoir,
la condition initiale est fixée par le condensateur -> uc(0)=0 donc i(0)=?
Je ne vois pas quoi conclure ici... Mais j'ai essayé de bricoler quelque chose pour trouver un lien entre di/dt et du/dt :
Déjà, i2(0) = 0, donc i(0)=i1(0).
En faisant une loi des mailles, on a 0 = E - Ri - u. En dérivant le tout, on a di/dt(0) = -du/dt(0)*1/R.
Or, C*du/dt(0) = i(0) = E/R, d'où di/dt = -E/(R²C) ?
Pour vous mettre sur la piste:
pour trouver la condition initiale sur la dérivée du courant i il faut se servir de la continuité de la tension aux bornes du condensateur.
uc(t0-)=uc(t0+)=0
uc(t)=Ri(t)+Ldi/dt
donc di/dt(t0+)=?
Du coup di/dt(0+) = -E/L.
Mais je ne vois pas comment on arrive à l'égalité uc(t)=Ri(t) + Ldi/dt. Ni pourquoi ce que j'ai fait est faux..
J'ai écrit une anerie, il fallait lire uc(t)=Ldi/dt évidemment.
Cela vous débloque la situation?
Comme uc(0) = 0 on trouverait di/dt(0) = 0, c'est pourtant ce que j'avais trouvé au début ?
Il y a le courant i qui circule dans R, le courant i1 qui circule dans L et i2 qui circule dans C.
Il faut donc lire uc=Ldi1/dt
et i2=i-i1
Que vous écriviez di1/dt(t0+)=0 soit mais pas di/dt(t0+)=0
