J'ai d'autres questions sur la poussée d'Archimède

[Poincare2poin0]

Bonjour,
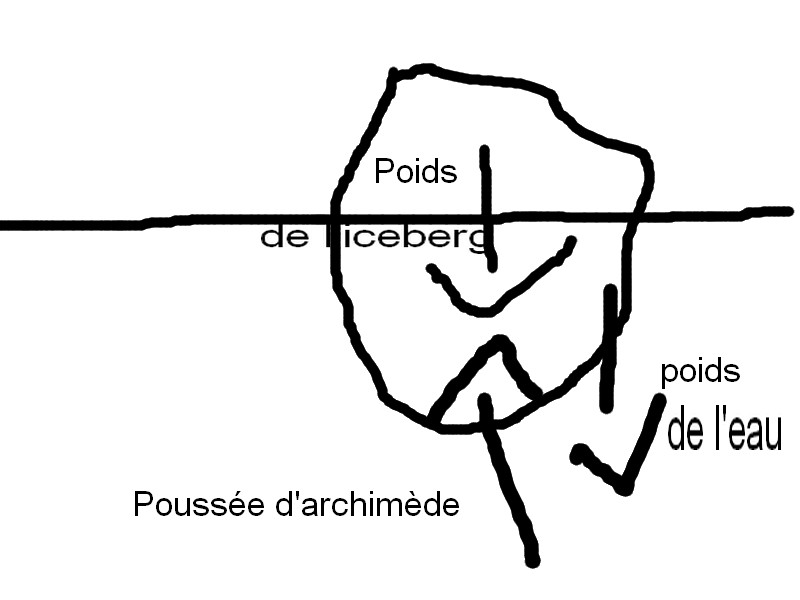
J'ai vu dans un livre que pour calculer le taux d'immersion d'un iceberg il fallait divier la poussée exercée par l'eau par la poids de l'iceberg.
E/P=Vi x ds x g/Vt x dd xg = Vi x ds/ vt x dd => Vi/VT=E x Dd / P x d puis on arrive à une égalité que je comprends dd/ds x 100
E = poussée de l'eau
P=poids de l'iceberg
Vi=V immergé
Vt= Volume total
ds= densité eau salée
dd= densité eau douce

Mes questions sont :
Comment arrive-t-on à l'égalité de la double flèche ?
Pourquoi doit-on calculer un rapport et pas une soustraction : la poussée de l'eau moins le poids de l'iceberg
ET L'accélération gravitationnelle ne devrait-elle pas diminuer la poussée d'arcimède puisque la terre étant plus lourde que l'eau elle devrait exercée une force du haut vers le bas et donc diminuer la poussée d'archimède ?

Mes questions peuvent paraître un peu bête mais je ne comprends pas :/
Merci d'avance

Ps: Désolé pour les fautes d'orthographe je suis pressé
-----

[LPFR]

Bonjour.
Utiliser des ‘x’ pour indiquer un produit était correct (en école maternelle) quand il n’y avait pas de variables littérales mais de nombres.
Le ‘x’ est une variable comme toutes les autres.
Ce qui rend vos équations inhabitables.
Je ne comprends pas que les enseignants tolèrent (et pratiquent) ce type d’écriture.
Au revoir.

[Dynamix]

ET L'accélération gravitationnelle ne devrait-elle pas diminuer la poussée d'arcimède puisque
1_la terre étant plus lourde que l'eau
2_elle devrait exercée une force du haut vers le bas
3_et donc diminuer la poussée d'archimède ?

1_La terre est plus lourde que l' eau ??? Pas compris .
2_C' est le cas , on nomme cette force "poids"
3_Si la gravité est plus forte , le poids de l' eau est aussi plus grand et donc la poussée d' Archimède aussi .
En contrepartie le poids de l' objet augment de la même façon .

[Poincare2poin0]

2_C' est le cas , on nomme cette force "poids"

J'y avais pas pensé je suis bête :/

3_Si la gravité est plus forte , le poids de l' eau est aussi plus grand et donc la poussée d' Archimède aussi .
En contrepartie le poids de l' objet augment de la même façon .

Oui mais la poussée est effectuée du bas vers le haut hors la terre étant l'objet le plus lourd elle exerce une "force" contraire à la poussée d'Archimède il faudrait donc ces deux poids (eau+iceberg) qui figurent sur les calculs : quelque chose du style Poids eau + poids iceberg / Poussée d'archimède (je n'ai pas de tablettes pour dessiner mais j'ai essayé de faire un dessin)


Utiliser des ‘x’ pour indiquer un produit était correct (en école maternelle) quand il n’y avait pas de variables littérales mais de nombres.

Ok je le réécris ^^

E/P=Vi * ds x g/Vt x*dd xg = Vi *Ds/ vt * Dd => Vi/VT=E * Dd / P * Ds
Merci d'avance

[A voir en vidéo sur Futura]

[Poincare2poin0]

Plus personne ?

[invite07941352]

Bonsoir,
Mes remarques en regardant de loin ( pour l'instant ) votre problème ... Qu'il faudra peut être bien retranscrire en entier et complet , plutôt que de dire " j'ai vu dans un livre ..." .
C'est quoi " le poids de l'eau " ??? Ici, c'est un simple problème d'Archimède et l'on n'emploie jamais cette expression , donc utilisez la bonne expression .
Je regarde les données : on dirait que c'est un glaçon d'eau douce ( oui ou non ? ) qui flotte dans l'eau salée ( oui ou non ?) .
A quoi peut servir la densité de l'eau douce ???
On ne parle pas de la densité du glaçon ( étonnant ...) , qui n'est pas celle de l'eau douce , jusqu'à preuve du contraire .
Votre figure n'apporte rien, au contraire , encore une fois , c'est quoi ce poids de l'eau ???
Donc, si vous pouvez expliquer toutes ces anomalies ...
Quand un glaçon flotte en surface , il est en équilibre entre son poids et la poussée d'Archimède .

[Poincare2poin0]

Je m'excuse d'être si peu précis :/
C'est un iceberg donc bien de l'eau douce qui flotte dans de l'eau salée. Donc la densité de l'eau douce est celle de l'iceberg. Je ne sais pas comment expliquer le poids de l'eau. Bon, je vais essayer : L'eau ayant une masse elle est attirée part la Terre et c'est donc cela que je cherche à exprimer par le "poids de l'eau".
EN plus de ce problème de force (c'est le cas de le dire) j'ai un problème mathématiques :
Ah non en fait je viens de résoudre le problème c'était tout bête et j'ai résolu aussi un autre problème en réflechissant juste 2sec --' (pardon de vous avoir dérangé)
Cependant il reste la question : le "poids de l'eau" n'est pas pris en compte ou est-ce une erreur de raisonnement de ma part ? (je pense à la deuxieme solution mais j'aimerai qu'on m'explique pourquoi)

Merci en essayant cette fois ci d'être clair et précis

[invite07941352]

Re,
L'eau remplit les lavabos, les baignoires, les océans et grâce à la gravité , reste à sa place .
L'air qui nous entoure , forme une couche d'environ 50 km d'épaisseur et grâce à la gravité , reste à sa place .
Les corps plongés dans l'eau , dans l'air subissent la poussée d'Archimède .
Un corps plongé dans le vide ne subit pas la poussée d'Archimède .
L'action de l'eau , de l'air s'arrête là pour ce genre de problème .
C'est déjà une bonne chose de ne pas savoir expliquer " le poids de l'eau " qui n'existe pas pour votre problème .

[Poincare2poin0]

Je dois vous paraître bête mais grâce à vous je crois avoir compris (malgré que ce soit un etat bien dangereux)
Merci de tout m'avoir expliqué

[gammler]

C'est un iceberg donc bien de l'eau douce qui flotte dans de l'eau salée.

Ca c'est secondaire . C'est surtout de la glace dans de l'eau, deux corps qui diffèrent par leur masse volumique. C-à-d que la glace est plus légère que l'eau, pour utiliser un langage trivial. C'est peut-être là que le "poids de l'eau" intervient. Si tu places le glaçon dans de l'huile, tu n'obtiendras pas le même résultat car l'huile est plus "légère" que l'eau. Elle exercera une pression moindre sur le glaçon.

[Poincare2poin0]

Non, c'est juste que j'avais mal compris mais le but des calculs etait de savoir le pourcentage immargé de l'iceberg
Merci pour vos réponses, explications

[le_STI]

Une petite précision qui pourrait aider: il manque des parenthèses dans la première formule.

Ce n'est pas:

E/P=Vi x ds x g/Vt x dd xg = Vi x ds/ vt x dd

mais:


Pour info ce quotient est égal à 1 puisque les forces se compensent (l'unité de E et P est le Newton).

Comment arrive-t-on à l'égalité de la double flèche ?

On fait passer et du côté gauche de l'égalité :
donne

Or on sait (ou on doit savoir, au choix ) que

On en déduit donc que

donc le rapport des volume est égal au rapport des densités.