Détermination du centre de gravité dans un triangle

[Zvoragor]

Bonjour,

Je suis en train de réviser pour ma seconde session (honte à moi) et je suis tombé sur un problème dont la solution n'est pas fournie dans mon livre, et, donc, dont j'ignore la réponse. Il faut déterminer la position x,y du centre de gravité d'un cheval positionné sur trois de ses jambes (Arrière gauche, arrière droite et avant droite. Les jambes arrière gauche et avant droite supportant chacune 1500N, et le poids total valant 5000N, j'en ai déduit que la jambe arrière droite supportait 2000N (très impressionnant, je sais))

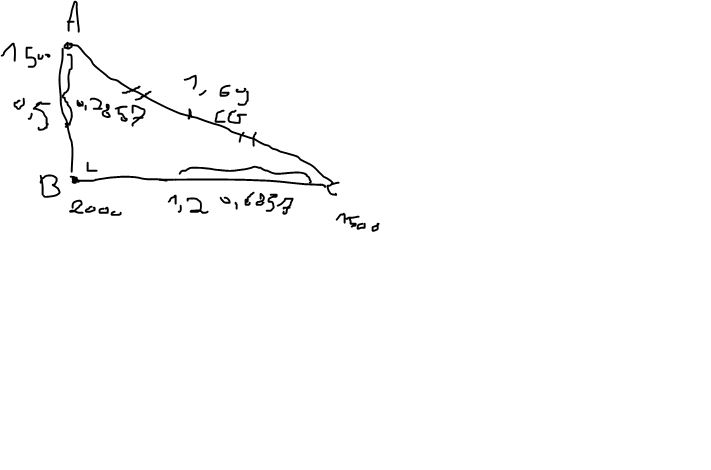
Pour commencer, j'ai cherché les CG de chaque côté, et j'ai trouvé : (petit dessin, les longueurs des segments AB et BC étaient donnés)



C.G AB se situe à 0.2857 et A
C.G de BC se situe à 0.6857 de C
C.G de AC se situe à équidistance des deux points, soit 0.845 de chaque

Et c'est là que ça coince, j'ai trouvé les points où les moments résultants sont nuls pour chaque "barre" prise indépendamment des autres, mais j'ignore totalement comment trouver les coordonnées X,Y du point où la somme des moments de force présents dans le triangle vaudrait 0, et ce même si je connais les coordonnées x,y des trois "cg locaux" (je sais pas comment les appeler du coup.)

Si quelqu'un pouvait m'expliquer, ça m'aiderait beaucoup, j'ai l'impression de passer à coté de l'essence même du problème.

(Il s'agit de mon tout premier message sur ce forum, j'espère avoir posté ce sujet dans la bonne catégorie et je m'excuse d'avance si jamais il y a une section réservée aux questions, je ne l'ai pas trouvée)
-----

[LPFR]

Bonjour et bienvenu au forum.
Le plus simple est décomposer le problème en deux : suivant l’axe des ‘x’ (je choisis BC) puis suivant les l’axe de ‘y’ (BA)

Pour les ‘x’, vous avez A et B confondus avec 3500 N et C avec 1500 N. Il s’agit de trouver le point pour lequel le moment des 3500 N se compense avec celui des 1500 N.
Cela vous donne la position du centre de gravité dans la direction des ‘x’.
Puis, pour les ‘y’, on confond B et A avec 3500 N. Il faut trouver le point sur ‘y’ pour lequel le moment des 3500 N de A+B se compense avec les 1500 N de C. Cela vous donne la position du centre de gravité en ‘y’.
Au revoir.

[Dynamix]

Salut

j'ai cherché les CG de chaque côté

Curieuse méthode .
Le triangle est fictif et les cotés n' ont pas de poids .

Pour résoudre ce genre de problème il n' y a qu' une méthode valable (sans doute celle qu' on t' a enseigné)

1_calculer la résultantes des 3 forces
2_calculer le moment de chaque force en un même point (en B par exemple , c' est pas mal )
3_calculer le moment total .
4_diviser le moment par la résultante pour trouver la position du CG par rapport au point de référence des moment .

Noter que :
_Les forces n' ont qu' une composante en Z , alors que les moments ont une composante X et une composante Y .
_On peut pour simplifier prendre comme axe x le coté BC

[Resartus]

Pour faire graphiquement ce genre d'exercice, on peut procéder en deux temps.
L'ensemble des deux jambes en A et C est équivalent à une force unique de 3000 N au CG soit le milieu de AC.
Ensuite on calcule le CG de cette force au milieu de AC avec la force en B.. Cela va donner un point sur la médiane en B au triangle.
Le plus difficile est de calculer la longueur de cette médiane...
On aurait pu commencer par n'importe quel coté du triangle, ce ne sera plus des médianes car les forces n'ont pas la même valeur, mais le résultat final sera le même


Sinon, la méthode la plus efficace est de calculer vectoriellement les coordonnées de ce CG.
On doit avoir en tout point O :

OG*5000=OA*1500+OB*2000+OC*150 0 (OG, OA, OB, OC sont des vecteurs)

On peut choisir un repère "facile" pour simplifier les calculs. On prend par exemple le répère de centre A et d'axes AB et AC, et cela va donner un résultat qui sera sous la forme OG=x*AB+ y*AC

Avez-vous déjà appris à faire ce genre de calculs vectoriels?

[A voir en vidéo sur Futura]