bonjours tous le monde
apres une grande recherche dans ce forum j'arrive finalement à comprendre cé quoi concretement une derivation et j'ai compris comment une derivée exprime le taux de variation, au math cé pas la pene de reconaitre ca mais quand je viens au physique je trouvais beaucoups de problemes et jé pas compris comment une derivée exprime la variation apres je comprend que f prime c'est egale à la tengante . brièvement j'arrive à comprendre la relation entre la derivée dans notre vie.
mais malheureusement je trouvais maintenant la meme probleme avec l'integration par exemple:
I={a b f(x).dx= F(a)-F(b)
(dsl mais jé pas trouvé le symbole de l'intergration alors je le remplace par { :entre a et b)
vraiment je comprend pas pourque et à cause de ca je trouvais beaucoup de probleme de comprendre la D.T.E car je pense que pour comprendre cette derniere on doit comprendre les relation non jute les apliquer
et mezci d'avance pour vos reponses
-----





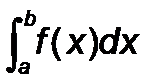 donc dx c'est une variation trés petite qu'on peut considerer comme largeur et on le multupie par la longeur "Sba f(x)" mais je comprends pas comment cette derniere represente la longeur
donc dx c'est une variation trés petite qu'on peut considerer comme largeur et on le multupie par la longeur "Sba f(x)" mais je comprends pas comment cette derniere represente la longeur

