
- Forum
- Futura-Sciences : les forums de la science
- MATIERE
- Physique
- Gain en tension pour un filtre avec AOP.
Gain en tension pour un filtre avec AOP.
- 14/01/2016, 16h23 #1invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Gain en tension pour un filtre avec AOP.
------

- 15/01/2016, 07h40 #2invite6dffde4c

- Date d'inscription
- janvier 1970
- Messages
- 43 330
Re : Gain en tension pour un filtre avec AOP.
Bonjour.
Vous vous compliquez la vie pour rien.
La contre-réaction fait que la tension sur la patte ‘-‘ sera égale à zéro.
Comme l’impédance de l’AO est infinie, tout le courant qui circule sur l’impédance d’entrée est égal à celui qui circule entre la patte ‘-‘ et la sortie.
Il suffit donc de calculer le courant d’entrée, puis la chute de tension sur l’impédance de la contre-réaction.
Une ou deux lignes de calcul. Pas plus.
Au revoir.
- 15/01/2016, 13h35 #3invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Re : Gain en tension pour un filtre avec AOP.
Ah ok,effectivement,c'estpeut être bon mais c'est long à écrire en effet,merci LPFR.Bonjour.
Vous vous compliquez la vie pour rien.
La contre-réaction fait que la tension sur la patte ‘-‘ sera égale à zéro.
Comme l’impédance de l’AO est infinie, tout le courant qui circule sur l’impédance d’entrée est égal à celui qui circule entre la patte ‘-‘ et la sortie.
Il suffit donc de calculer le courant d’entrée, puis la chute de tension sur l’impédance de la contre-réaction.
Une ou deux lignes de calcul. Pas plus.
Au revoir.
- 16/01/2016, 14h47 #4invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Re : Gain en tension pour un filtre avec AOP.
Bonjour,pour la question 2) on demande de tracer l'allure,mais je me demandais si il faut la tracer à partir des limites de |Vs/Ve| quand
 tend vers 0 et +l'infini?
tend vers 0 et +l'infini?
Ou il faut d'autres limites?
- Aujourd'huiA voir en vidéo sur Futura
- 16/01/2016, 14h59 #5invite6dffde4c

- Date d'inscription
- janvier 1970
- Messages
- 43 330
Re : Gain en tension pour un filtre avec AOP.
Bonjour.
Pour ω -> 0 le gain tombe à zéro et pour ω -> infini le gain aussi tombe à zéro.
Il est probable qu’entre les deux il y ait des choses intéressantes. Comme un maximum de gain, par exemple.
Au revoir.
- 17/01/2016, 15h00 #6invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Re : Gain en tension pour un filtre avec AOP.
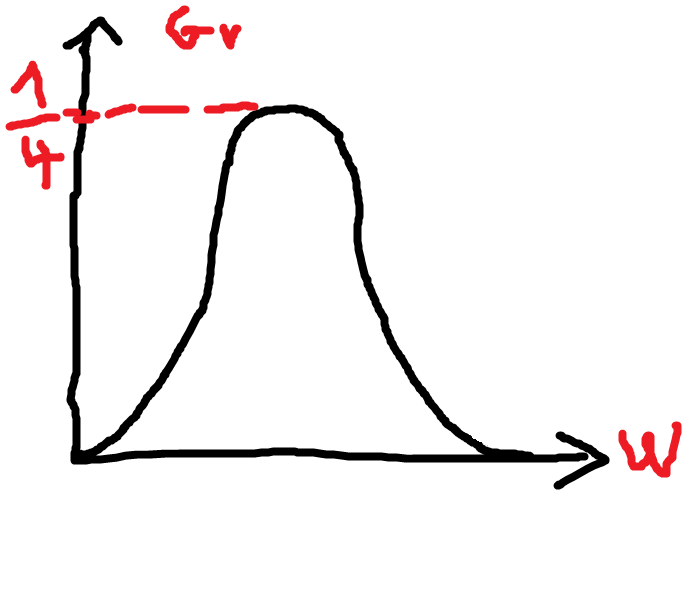
J'avais même pas vu que tu me mettais sur la piste,alors le gain est maximum quand le dénominateur est minimum donc quand -1/(rcw)+rcw=0=>w=1/rc Ce qui implique que le gain maximum vaut 1/4;(1/(1+1+2)).
Donc ça devrait donner ça l'allure:

- 18/01/2016, 09h55 #7curieuxdenature
- Date d'inscription
- mai 2005
- Âge
- 74
- Messages
- 5 125
Re : Gain en tension pour un filtre avec AOP.
Bonjour Argon39
A la fréquence Fo je trouve plutôt un gain de 1/2, c'est ce que laisse entendre la fonction de transfert quand la condition C1=C2=C et R1=R2=R. (T = 1 / (2 jA) )
Ta fonction de transfert n'est donc pas correcte, avec l'AOP dans le circuit, on n'a pas un filtre de Wien classique ( où T = 1/ (3 jA) ) parce que le montage est inverseur.
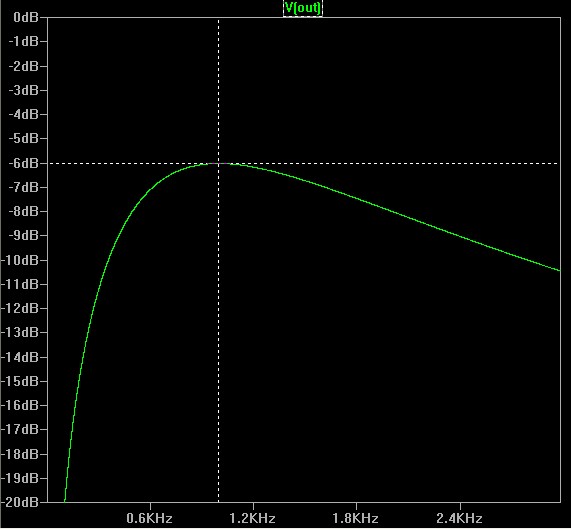
L'allure de la courbe est à peu près correcte, mais la pente descendante est bien plus douce (Axes des x et y en mode linéaire.)
Cliquez pour afficher
L'electronique, c'est fantastique.
- 18/01/2016, 15h05 #8invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Re : Gain en tension pour un filtre avec AOP.
Bonjour,en refaisant mes calculs je trouve aussi 1/2 effectivement.Bonjour Argon39
A la fréquence Fo je trouve plutôt un gain de 1/2, c'est ce que laisse entendre la fonction de transfert quand la condition C1=C2=C et R1=R2=R. (T = 1 / (2 jA) )
Ta fonction de transfert n'est donc pas correcte, avec l'AOP dans le circuit, on n'a pas un filtre de Wien classique ( où T = 1/ (3 jA) ) parce que le montage est inverseur.
L'allure de la courbe est à peu près correcte, mais la pente descendante est bien plus douce (Axes des x et y en mode linéaire.)
Cliquez pour afficher
Mais on m'a dit que ce que je trouve est correcte seulement pour un AOP idéal mais personnellement j'en sais rien.
Donc je vous crois peut être il y a-t-il une erreur dans mon raisonnement,en tout cas merci pour votre aide et pour la courbe .
.

- 18/01/2016, 15h27 #9invite6dffde4c

- Date d'inscription
- janvier 1970
- Messages
- 43 330
Re : Gain en tension pour un filtre avec AOP.
Bonjour.
C’est vrai que les hypothèses d’ampli idéal font que le résultat ne correspond pas à 100 % à la réalité. Mais il correspond peut-être à 99,99 %.
Alors, sauf pour des applications critiques, c’est la réalité à un chouia près.
Il ne fait pas oublier que la tolérance dans la valeur des composants réels est, ordinairement, de 5% pour les résistances et de 10-20% pour les capacités. On peut avoir mieux, mais il faut le payer.
Au revoir.
- 18/01/2016, 17h47 #10invite9c5f7482
- Date d'inscription
- janvier 1970
- Messages
- 659
Re : Gain en tension pour un filtre avec AOP.
Ah ok,on considérera donc que ça représente quasiment la réalitéeBonjour.
C’est vrai que les hypothèses d’ampli idéal font que le résultat ne correspond pas à 100 % à la réalité. Mais il correspond peut-être à 99,99 %.
Alors, sauf pour des applications critiques, c’est la réalité à un chouia près.
Il ne fait pas oublier que la tolérance dans la valeur des composants réels est, ordinairement, de 5% pour les résistances et de 10-20% pour les capacités. On peut avoir mieux, mais il faut le payer.
Au revoir. .
.
Sinon on me demande dans la question 3) d'estimer pour
pour  et l'infini.
et l'infini.
Je suppose qu'il demande le déphasage de |vs/ve| mais pour les deux limite,Gv=0 et on sait que vu que
vu que  pour les 2 limites.
pour les 2 limites.
Mais je sens que les mathématiciens et les physiciens de ce forum diron que n'existe pas!
n'existe pas!
On me demande aussi l'intérêt du filtre avec AOP,je chercherai encore...
- 18/01/2016, 20h18 #11invite6dffde4c

- Date d'inscription
- janvier 1970
- Messages
- 43 330
Re : Gain en tension pour un filtre avec AOP.
Re.
Quand vous étudiez une limite il faut la calculer « avant » la limite. Si vous écrivez sin(o)/0 vous avec une indétermination. Il faut écrire sin(x)/x et regarder comment ça évolue quand x -- > 0.
Pour votre ampli, vous pouvez dire que ωRC = x et demander à wolframalpha de vous faire le calcul et la courbe :
http://www.wolframalpha.com/input/?i=bode+plot+ix%2F%281+%2B+ix% 29^2
A+
- 19/01/2016, 10h58 #12curieuxdenature
- Date d'inscription
- mai 2005
- Âge
- 74
- Messages
- 5 125
Re : Gain en tension pour un filtre avec AOP.
Bonjour
Pour revenir la dessus, en simulation avec un AOP, je mesure un écart d'environ 45 µV entre le point milieu du filtre (la borne '-' de l'AOP) et la masse.
C'est si faible qu'on peut considérer la théorie comme étant exacte en posant que ce point est une masse virtuelle.
En situation réelle, il faudrait aussi mettre une résistance en série dans la branche '+', de valeur R1 en // sur R2, de plus comme c'est un exercice théorique, l'alimentation symétrique de l'AOP n'apparait pas non plus. Ce sont des détails inutiles pour les calculs.L'electronique, c'est fantastique.
- 19/01/2016, 11h06 #13invite6dffde4c

- Date d'inscription
- janvier 1970
- Messages
- 43 330
Re : Gain en tension pour un filtre avec AOP.
Bonjour.
Dans la réalité ça risque d’être bien pire à cause de la tension de offset des AOP ordinaires.
Mais toujours négligeable dans la plupart d’applications.
Au revoir.
Discussions similaires
-
Problème avec gain en tension
Par invite09104ce0 dans le forum PhysiqueRéponses: 8Dernier message: 22/10/2013, 13h56 -
Filtre passe bande avec gain 20
Par invite5c711ba9 dans le forum ÉlectroniqueRéponses: 4Dernier message: 10/04/2009, 16h26 -
Filtre et gain
Par invite59c3ef45 dans le forum PhysiqueRéponses: 0Dernier message: 25/01/2009, 17h41 -
filtre avec résistances commandées en tension
Par invitecf1974fd dans le forum ÉlectroniqueRéponses: 7Dernier message: 20/06/2008, 15h24 -
formule gain en fonction de la freq pour un filtre
Par invite945e8d31 dans le forum ÉlectroniqueRéponses: 3Dernier message: 03/12/2007, 22h34
Fuseau horaire GMT +1. Il est actuellement 08h18.

