Centre de masse, d'inertie, barycentre

[Charlycop]

Bonjour à tous,

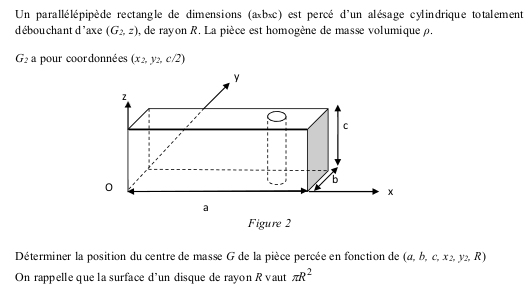
Prenons un parallélépipède rectangle homogène de côtés a, b, c et de masse m et ayant son coin en bas à gauche à l'origine d'un repère cartésien, puisque le centre géométrique sera le centre de masse, on aura :


Dans mon cours, on me balance la formule suivante pour le calcul du barycentre :


Je ne comprends pas comment l'appliquer.

Quelqu'un serait-il assez sympa pour me détailler me détailler la méthode ? (j'ai peut-être simplement du mal à lire la formule)

Merci d'avance !
-----

[LPFR]

Bonjour.
Elle est curieuse la formule de votre cours.
Quand c’est une somme, il faut utiliser de petites masses et non des différentielles, ce qui demande un nombre infiniment grand de masses.
On écrit alors des intégrales et on tombe sur la vraie définition du centre de masses.
Pour un nombre fini de masses on devrait vous donner :


Cela veut dire que quand vous avez un objet formé de N masses ponctuelles mi, le centre de masses est celui donné part la formule. Vous pouvez ainsi calculer le centre de masses d’une galaxie (en considérant les étoiles comme masses ponctuelles).

Mais dans le cas général, il faut passer par des masses infiniment petites (des différentielles ‘dm’) et la définition du centre de masses devient :



Cette fois vous pouvez diviser l’objet en petit bouts de volume de la forme qui vous chante avec la seule condition que le vecteur qui va de l’origine à la masse puisse être considéré comme constant dans tout la petite masse ‘dm’.

Vous trouverez une explication plus détaillée et plus utilisable dans le chapitre 6 de ce fascicule :
http://www.sendspace.com/file/ttrwye Cliquez sur: download

Au revoir.

[Dynamix]

Salut
Comme dm = ρ.dv
avec un solide homogène ρ est constant et tu peux le sortir de la somme .
Comme il figure en haut et en bas , il s' élimine .

[Charlycop]

Bonjour,

Voici un exercice, voici ma réponse, j'aimerai votre critique, si vous le voulez bien.



Ma réponse :
--------------
Masse m₁ de l'objet sans trou : m₁ = ρabc
Coordonnées du centre de masse original : G₁(a/2, b/2, c/2)

Masse m₂ du cylindre en moins : m₂ = ρπR²c
Coordonnées du centre de masse dy cylindre : G₂(x₂, y₂, c/2)


Donc, sur x, on a :


et ensuite, je propose de faire la même chose sur y, qu'en pensez-vous ?

[A voir en vidéo sur Futura]

[LPFR]

Bonjour.
La formule est mauvaise (signes) et mal appliquée.
Regardez la formule du fascicule dont je vous ai donné la référence.

Et par la suite il faut l’appliquer pour ‘y’ et non ‘xy’.
Au revoir.

[Titiou64]

Bonjour Charlycop,

Personnellement, je trouve la même formule que toi...

[LPFR]

Re.
Oui. Désolé, j’ai oublié qu’on enlève la masse du trou.
Mes excuses.
A+