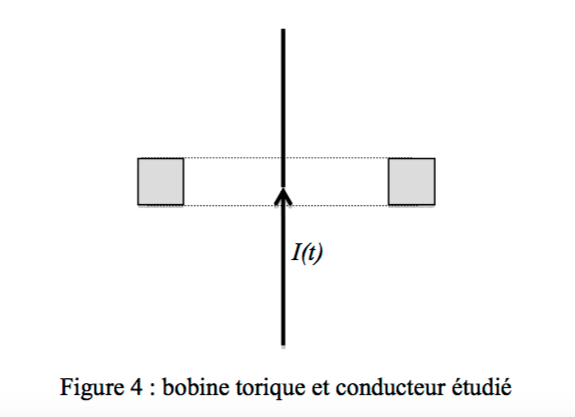
On a un tore avec un courant variable Im=cos(wt) qui passe selon ez.
Il faut justifier un courant i(t) dans le bobinage torique. C'est parce que le courant Im est variable, qu'il crée un champ magnétique variable qui d'après Maxwell crée un champ électrique variable, qui recrée un champ magnétique variable qui crée i(t) ?
Ou je vais trop loin ?
Bjr à toi,
Mais en général ça dure pas !! ( auto-induction)
Bonne journée
Bonjour,
Je vous remercie pour votre réponse.
Mais en fait ma proposition je n'en suis pas trop sûr, j'aimerai rédiger proprement mais c'est un peu difficile.
Pouvez vous m'apportez plus de détails ?
Rédigé proprement, si je dis : "Le courant I(t) variable est associé à un champ magnétique variable et crée d'après les équations de Maxwell un champ E (rot B = y0(j+espilon0 * dE/dt)), champ E variable qui va lui-même créer un champ magnétique variable dans le tore (rot E = -dB/dt). C'est le principe d'induction."
Est-ce correct ? D'ailleurs l'auto-induction agit également sur l'axe (Oz), non ?
Bonjour.
L’ordre est : le courant I(t) crée un champ magnétique variable qui donne un flux magnétique variable à l’intérieur de la bobine torique.
Ce flux variable induit (loi d’induction de Faraday) une tension sur le extrémités de la bobine.
Remarquez que ce qui est induit est une tension. Le courant dépendra de ce qui est branché sur les extrémités de la bobine.
Au revoir.
Bonsoir,
Je vous remercie pour votre réponse !
D'après la formule de mon cours je vois pourquoi c'est une tension qui est induite, e=-dflux/dt
Cependant, pourquoi est-ce que le courant dépendra de ce qui est branché aux extrémités ? Dans l'exercice le tore est entièrement rebouclé sur lui-même.
Bonjour.
Dans ce cas, ce qui est branché aux extrémités est un court-circuit.
Mais pour calculer le courant il faudra tenir compte non seulement de la résistance du bobinage si ce n’est pas un conducteur idéal, mais aussi du fait que dans la formule de l’induction de Faraday :
E = N ∂Φ/∂t
Dans le Φ il faut inclure non seulement le flux crée par le courant I(t) mais celui crée part le courant induit lui-même.
Si la résistance totale du bobinage court-circuité est nulle, le courant dans le bobinage sera tel qu’il n’y aura pas de variation de flux dans le tore, car le E dans la formule est nul.
Au revoir.
Bonjour,
Je reviens sur ce vieil exercice.
On me demande de montrer en utilisant les propriétés de symétrie de la distribution de courant que le champ magnétique est nécessairement orthoradial, et de montrer à l'aide des invariances qu'il se met sous le forme.
B = Bthéta (r,z,t) * ethéta
Sachant B le champ magnétique total créer par le courant I(t) dans le fil et i(t) dans la pince.
Je ne vois pas comment résoudre cette question sans dire que l'on est dans l'ARQS, on est obligé de le dire je me trompe ?
Et comme on est dans une bobine on utilise l'ARQS magnétique pour les équations de Maxwell et on ne se soucie plus de t pour les invariances et symétrie. Ai-je raison ?
Je vous remercie par avance.
Re,
J'ai une ou deux autres questions.
Par le suite on nous demande de calculer B, et par un contour passant par M un point dont les coordonnées sont r entre 2a et 3a et z entre -a/2 et a/2 j'obtiens le champ suivant :
B(t) = mu0 * (I(t) + N*i(t)) / (2*pi*r) ethéta
On me demande de calculer l'expression du flux du champ magnétique à travers une spire du tore.
Je fais donc double intégrale de B et dS et j'obtiens : Phi(t) = mu0 * (I(t) + N*i(t)) * a^2 / (2*pi*r)
Mes questions sont donc : Sachant divB = 0 et donc la double intégrale de B à travers toute surface fermée est nulle, qu'est-ce qu'une surface fermée précisément, une surface qui délimite un volume ? La surface d'une spire est la surface s'appuyant sur le contour de cette spire et vu que je n'obtiens pas 0 j'en déduis qu'elle n'est pas fermée.
Enfin on me demande d'en déduire le flux total à travers les N spires du tore.
Dans mon cours j'ai : flux total = flux extérieur + flux propre (avec flux propre toujours négligé sauf dans le cas d'une self)
Je sais qu'on peut lier le flux au coefficient L mais je n'arrive pas dans le cas présent à retrouver le L que l'on me donne :
Capture d’écran 2016-04-28 à 18.21.30.png
Je vous remercie par avance.
Bien à vous,
Capture d’écran 2016-04-28 à 18.13.59.png
Bonjour.Envoyé par Tirlititi
Bonjour,
Je reviens sur ce vieil exercice.
On me demande de montrer en utilisant les propriétés de symétrie de la distribution de courant que le champ magnétique est nécessairement orthoradial, et de montrer à l'aide des invariances qu'il se met sous le forme.
B = Bthéta (r,z,t) * ethéta
Sachant B le champ magnétique total créer par le courant I(t) dans le fil et i(t) dans la pince.
Je ne vois pas comment résoudre cette question sans dire que l'on est dans l'ARQS, on est obligé de le dire je me trompe ?
Et comme on est dans une bobine on utilise l'ARQS magnétique pour les équations de Maxwell et on ne se soucie plus de t pour les invariances et symétrie. Ai-je raison ?
Je vous remercie par avance.
La symétrie ne suffit pas.
Le problème a un axe de symétrie de rotation mais il a aussi une symétrie de translation le long de cet axe.
Ce que l’on peut conclure à partir de la symétrie de rotation est que si le champ avait une composante radiale, elle serait la même tout autour de l’axe de symétrie et tout le long de l’axe (à cause de la symétrie de translation).
Cette composante radiale impliquerait que la divergence de B serait non nulle, ce qui serait en contradiction avec les lois de Maxwell.
Car cela impliquerait de la divergence de B serait non nulle.
Le problème est que je ne suis pas sur que vous ayez étudié les lois de Maxwell.
Mais c’est la seule façon que je vois d’exclure une composante radiale.
Pour ce qui de la composante axiale (parallèle au conducteur) de B, je ne sais pas comment l’exclure à partir de la symétrie.
La façon la plus simple de montrer que le champ est tangentiel, est de faire appel à la loi de Biot et Savart. Mais il faut, un fois encore que vous l’ayez vu en cours.
Oui. Vous êtes en régime quasi stationnaire.
Je vous ai déjà dit que ce qui s’induit dans la bobine n’est pas un courant mais une tension. Le courant dépend de ce que l’on branche sur la bobine. Si on la court-circuite, alors le courant dépendra de la résistance de la bobine.
Et si de plus la bobine est supraconductrice, alors, le flux dans le tore sera constant, et le courant dans la bobine aura la valeur qu’il faut pour annuler le flux produit la le conducteur axial.
Pour les invariances je m’abstiens. Je ne les utilise pas.
Au revoir.
Re.
Votre Phi est mal calculé. Vous n'avez pas intégré B. Vous l'avez multiplié par la section du tore, comme s'il ne dépendait pas de 'r'.
A+
Bonjour,
Je vous remercie pour cette longue réponse, claire et précise. J'apprécie votre aide.
On a vu la loi de Biot et Savart en cours seulement notre prof nous a dit de l'utiliser en dernier recours après le théorème d'ampère.
Et il est mentionné dans la question d'utiliser invariances et symétries.
Ce n'est pas précisé dans l'énoncé pour le régime quasi stationnaire, je dois le mentionner non ?
Concernant les invariances et symétries je dis qu'une fois qu'on est en régime quasi stationnaire (et donc que je ne tiens plus compte de t pour mes invariances et symétries), tout plan contenant l'axe Oz est plan de symétrie. Ainsi c'est un plan d'antisymétrie pour B qui est donc perpendiculaire à tous ces plans. Et par conséquent il est orthoradial.
Et j'utilise les invariances pour dire que c'est invariant par toute rotation selon tétha et ainsi on obtient B = Bthéta (r,z,t)
Si mon raisonnement est faux n'hésitez pas à me le dire. (je ne me suis pas servi des lois de Maxwell effectivement pour déterminer l'expression littérale de B)
La bobine est court circuité ici on s'en sert comme pince ampèremétrique, et elle a une résistance, donc il y a un courant d'après ce que vous m'avez dit.
Vous n'avez pas répondu pour les questions de mon deuxième post, je ne sais pas si vous l'avez vu.
Je vous remercie pour votre aide.
Bien à vous,
En effet, j'ai voulu intégrer trop vite, je vous remercie pour votre précision.
En recalculant j'obtiens : Phi(t) = mu0 * (I(t) + N*i(t)) / (2pi) * a * ln(3/2)
Car on intègre 1/r dr de 2a à 3a.
Ainsi mon Phi se rapproche bien plus de ce à quoi ressemble L et M. Savez vous comment je peux les déterminer ?
Je vous remercie.
Pour avoir Phitotal(t) on multiplie donc par N vu qu'il y a N spires.
Je pense avoir trouvé, L serait la partie de phitotal qui s'exprime en fonction de i(t) et M celle qui s'exprime en fonction de I(t).
Par contre je ne sais pas vraiment pourquoi. Dans cet exercice il n'y a pas de notion de flux extérieur et flux propre ou si ? Ce sont des choses que l'on n'a pas souvent vues en cours.
Et ma justification n'est que purement visuelle vu qu'ils donnent les résultats de L et de M mais nous demande comment les retrouver. Je suppose que M est en rapport avec le champ magnétique extérieur (celui qu'on obtient depuis le fil) et L en rapport avec le champ magnétique qu'on obtient depuis le courant i(t) du tore.
Je vous remercie par avance.
Re.
‘L’ doit être d’inductance (auto-inductance, self) de la bobine du tore.
Et ‘M’ peut être l’inductance mutuelle entre le conducteur central et la bobine du tore.
Mais je trouve un peu « surprenant » de calculer l’inductance ou l’inductance mutuelle d’une bobine court-circuitée.
A+
Re,
C'est juste pour un concours ca doit être pour tester nos connaissances.
Ce sont bien l'auto-inductance et la mutuelle inductance. Mes raisonnements sont donc justes ?
Ca me ferait vraiment plaisir et m'aiderait si vous pouviez répondre à ces deux questions :
-Ce n'est pas précisé dans l'énoncé pour le régime quasi stationnaire, je dois le mentionner non ?
-Sachant divB = 0 et donc la double intégrale de B à travers toute surface fermée est nulle, qu'est-ce qu'une surface fermée précisément (qu'on doit avoir pour utiliser le théorème de la divergence), une surface qui délimite un volume ? La surface d'une spire est la surface s'appuyant sur le contour de cette spire et vu que je n'obtiens pas 0 (j'obtiens la résultat que vous m'avez fait recalculé), elle n'est donc pas fermée.
Bonjour.
- Ça ne peut pas faire de mal de le rappeler. Même si pour ce type de problème c’est évident.
- Oui. Une surface fermée est celle qui entoure complètement un volume. Que vous pourriez remplir d’eau ou d’un gaz, sans qu’ils s’échappent.
Je ne vois pas ce que la divergence vient faire dans ce problème (à part la justification de la nullité de la composante radiale du champ).
Ici c’est la loi d’Ampère qui vous permet de déterminer le champ produit par le conducteur central d’un côte, et par les spires du tore d’un autre côté.
La surface utilisée est celle délimitée par le chemin de l’intégrale de B. Dans les deux cas c’est un disque de rayon ‘r’ (dans vos formules).
Au revoir.
Bonjour,
Je vous remercie pour vos 2 réponses, c'est exactement ce que je souhaitais !
Je parlais de la divergence de B car pour calculer le flux de B à travers une spire on fait la double intégrale de BdS, or dans le théorème de la divergence si la surface est fermée on obtient double intégrale sur surface fermée de BdS = triple intégrale de divBdT sur le volume délimité par la surface qui vaut 0.
Et comme le flux de B à travers une spire n'est pas nul, j'en ai déduit que ma surface n'était pas fermé. Je voulais donc un éclaircissement sur la définition de surface fermée, que vous m'avez apporté.
Dans la suite du problème on me demande en utilisant les notations complexes de définir H = i / I
Sachant I le courant dans le fil égal à
Et i(t) celui dans le tore égal à
On doit déterminer la fonction de transfert en fonction de L, M, w et R la résistance du tore.
Je suppose qu'on doit de servir de i(t) = L * di(t)/dt / R pour le numérateur mais je ne vois pas comment exprimer ma fonction de transfert seulement en fonction de L, M, w et R.
Avez-vous une idée ?
Je vous remercie par avance.
Bien à vous,
Re.
Une intégrale de surface peut être une intégrale double. Mais ce n’est pas nécessaire. Cela dépend si le différentiel de surface est de premier ordre (L.dx) ou de deuxième ordre (dx.dy).
Même chose pour le volume. Si le différentiel est de troisième ordre (comme dx.dy.dz) alors c’est une intégrale triple. Mais ça peut être une intégrale double (L.dx.dy) ou simple (S.dx). Je ferme la parenthèse.
Le flux magnétique à travers une surface quelconque est l’intégrale de. Si la surface est fermée alors, bien sur, le flux est nul, à cause de la div B = 0.
Ici la surface qui vous intéresse est la section du tore, qui est un petit carré.
Le flux à travers une surface fermée n’est intéressant qu’en électrostatique où l’on peut utiliser le théorème de Gauss : « ce qui sort d’un volume est égal à ce qui se crée dedans ». En magnétostatique il ne sert à rien (on arrive à 0 = 0). Car il n’y a pas des sources de champ magnétique (des monopôles).
Dans votre problème (tordu) le flux dans le tore est nul. Simplement à cause de la loi de Faraday. Comme la bobine est court-circuitée et que sa résistance est nulle ∂Φ/∂t est aussi nul. Et comme Φ ne peut pas être continu, car vous n’avez du courant continu dans le conducteur central, cela implique que Φ est nul. Mais c’est parce qu’on utilise une bobine supraconductrice.
Et je vous rappelle que le flux dans le tore est nul car le courant induit dans la bobine est tel qu’il doit maintenir le flux nul.
On vous demande d’utiliser de la notation complexe pour quoi faire ?
En général, quand on travaille avec des selfs (inductance) ou des condensateurs, la notation complexe simplifie les calculs. Mais ici, elle me semble totalement inutile. D’autant plus qu’il n’y a pas de déphasage entre les deux courants (si la bobine est toujours court-circuitée)
A+
@ LPFR : le courant varie, il y a donc induction, sinon, il serait inutile d'utiliser des fonctions de transfert.
@ Tirlititi : Remplacez les d/dt dans vos équations différentielles en t par des j.w et vous aurez la fonction de transfert demandée.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Re,
Je vous remercie pour ce gros détail sur les intégrales, j'ai bien compris ce que je voulais comprendre.
Je ne pense pas que le flux est nul dans mon problème. Corrigez moi si je me trompe ci-dessous, je vais essayer d'expliquer ce que je pense.
e=-dΦ/dt et sachant mon Φ obtenu #13 : Phi(t) = mu0 * (I(t) + N*i(t)) / (2pi) * a * ln(3/2)
On obtient Phitot(t) en multipliant par N puisque j'avais fait le flux à travers une spire seulement.
Ainsi e = - mu0*N*dI(t)/dt *a * ln(3/2) / (2pi) - mu0*N*di(t)/dt *a * ln(3/2) / (2pi)
Ce qui donne si l'on utilise L et M : e = - (MdI(t) + Ldi(t))
Vous avez dit que la résistance de la bobine était nulle, or elle vaut R.
Du coup je comprends mal votre avant dernier paragraphe, mais ca doit être parce que le problème est tordu. (Je vous donne le sujet si cela peut vous aider, c'est le troisième problème vous serez familiers avec toutes les questions jusqu'à celle que je pose vu que vous m'avez aidé à les résoudre : sujet)
Je vous remercie de m'aider, c'est vraiment gentil !
Re.
Depuis le début vous m’avez laissé croire que la bobine était court-circuitée.
Si maintenant la bobine est branchée sur une résistance R, le courant qui y circule est égal à la tension induite (sans oublier ce même courant) divivée par la résistance.
J’arrête pour le moment.
Peut-être que je reviendrai quand je me serai calmé.
A+
Re,
Je suis vraiment désolé ce n'était pas mon but, mais je n'ai jamais vu des circuits de ce genre. Pour moi un tore étant rebouclé sur lui-même, je ne vois pas comment on pourrait le brancher sur autre chose. De plus, pour moi lorsque la résistance interne du tore n'est pas quelque chose sur lequel il serait bouclé. Pour ainsi dire, je pense que je n'ai pas moi même compris le circuit, j'hésite entre :
- un tore branchée sur une résistance R comme vous le dites
- un tore dont la résistance interne est R branché sur rien du tout
Après c'est peut-être que je comprends mal le concept de résistance interne.
Je vous remercie tout de même pour toute l'aide apportée.
Si quelqu'un d'autre aurait la gentillesse de m'aider, je lui en serai reconnaissant.
Je pense que pour ma fonction de transfert H = i/I on peut exprimer i = Ldi(t)/dt / R ou -Ldi(t)/dt / R (je penserai plus pour le second dû à la formule e = -dΦ/dt mais j'aimerai avoir une confirmation)
Par contre pour exprimer I(t) en foncion de L,M, w et R je bloque. Pourtant je suis pas loin du but je pense, est-ce en lien avec la mutuelle inductance ?
En effet si je veux exprimer I = Tension/Résistance il me faudrait la tension et la résistance mais je ne pense pas que la résistance soit également R.
J'apprécierai réellement comprendre cette question.
Bien à vous,
Il me semble que vous avez tout.
La fem induite et d'auto induction e.
La loi de maille et la loi d'Ohm avec la résistance.
Votre tore présente une résistance R et on le court-circuite sur un ampèremètre de résistance nulle.
Vous pouvez donc trouver la relation entre i et I, en temporel, puis en complexe.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Bonjour,
Je vous remercie pour votre réponse.
Reprenez moi si je me trompe mais quand on dit qu'on court circuit le tore sur un ampèremètre de résistance négligeable c'est comme si on avait un circuit avec une seule résistance R rebouclé et avec un courant i(t) dedans non ?
Et donc dans mon cas la tension de cette résistance est le e que j'ai calculé ?
C'est bien cela.
On modélise en séparant les aspects inductifs des aspects résistifs et on met les deux en série avec le court-circuit.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Je vois bien le circuit, par contre je crois que j'ai des difficultés avec le concept de court circuit.
Comment le courant peut-il circuler sans générateur ? C'est parce que l'auto induction va entrainer les charges tout le temps ?
Et pour calculer la tension de l'aspect inductif, vous prenez e = - d phi / dt avec le phi qui comprend le flux extérieur à savoir l'apport de I(t) et du fil ou vous ne considérez pas cet apport ?
Quelqu'un aurait une idée s'il vous plait ?
Je peux avec plaisir étayer mes propos si mes questions ne sont pas claires. J'apprécierai réellement résoudre cette question.
Bien à vous,
Bonjour.
Joignez l’énoncé original et complet du problème et non la version interprété par vous.
Ça nous fera gagner du temps.
http://forums.futura-sciences.com/ph...s-jointes.html
Au revoir.
Bonjour,
Je vous l'ai donné dans mon commentaire #21.
Ce n'est pas cela dont vous parlez lorsque vous vouliez l'énoncé original ?
Je vous remercie.
