Trous d'Young et intensité lumineuse.

[Tirlititi]

Bonjour,

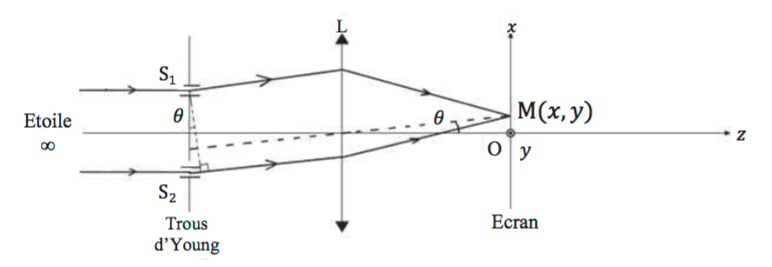
J'ai un exercice sur les trous d'young avec le schéma suivant :



La question est :

On rappelle que les capteurs optiques quadratiques fournissent un signal proportionnel à l'intensité lumineuse, cad proportionnel à la moyenne du carré du signal notée

On donne la formule de linéarisation suivante :
On donne aussi l'intensité lumineuse de chacune des ondes.

Exprimer l'intensité lumineuse au point M en fonction de et de la différence de marche entre les deux chemins optiques.

Je n'ai absolument jamais fait ca du coup ca m'arrangerait si l'un de vous pouvait me donner la réponse et m'expliquer comment on le calcule.
Pour la différence de marche, je sais que par le principe de retour inverse de la lumière (PRIL) appliqué en M, et le théorème de Malus, on obtient



Je vous remercie par avance pour votre aide.
-----

[LPFR]

Bonjour.
Encore un problème simple rendu merdique par la façon de le poser.
Le problème est celui classique des trous de Young avec diagramme de diffraction à l’infini (sans la lentille) (diffraction de Fraunhofer).
La lentille faut converger en un seul point sur le plan focal tous les rayons qui ont une même direction. Cela évite, en pratique de devoir placer l’écran trop loin.
Donc, il faut savoir que le chemin optique de tous le rayons qui vont de la ligne pointillée entre S1 et S2 et le point focal est le même. Donc, la différence de marche δ entre les deux rayons est la petite distance donnée par l’angle θ au niveau bas.

Au niveau de l’écran on a deux rayons qui arrivent avec une différence de marche δ.
Donc les amplitudes sont de la forme
cos(ωt) et cos(ωt ± δ)
Et c’est avec ça qu’il faut utiliser les formules données.
Au revoir.

[Tirlititi]

Bonjour,
Je suis désolé que tous mes problèmes soient mal posés, il faut croire que je n'ai pas de chance.
Je vous remercie pour votre aide.

Ce que je ne comprends pas bien est que l'on nous parle jamais du champ électrique. J'ai un moyen d'obtenir l'éclairement dans mon cours avec :
la puissance traversant une surface.
Et l'éclairement est cette même valeur divisée par la surface.
Donc avec l'expression de E je pourrais m'en sortir mais avec I je n'ai pas de formule. :/

Est-ce que je dois sommer et en faire la valeur moyenne pour obtenir l'éclairement ?
J'aimerai savoir quelle est la formule à utiliser en fait, n'ayant pas dans mon cours une formule partant de I.

Je vous remercie.

[LPFR]

Re.
Le champ électrique d’une onde plane est bien donné par la formule de votre cours.
Mais ça vous fait une belle jambe. Vous ne connaissez pas la puissance par unité de surface.
Mais vous n’a avez pas besoin.
Et ce qui varie avec ωt n’es pas l’intensité, mais la valeur instantanée du champ électrique :
E1 = Eo.cos(ωt) et E2 = Eo.cos(ωt ± δ)
L’amplitude (sans la dépendance avec le temps) du carré de l’addition de ces deux termes est l’intensité.
A+

[A voir en vidéo sur Futura]

[Tirlititi]

Re,
Je connais en effet le champ électrique d'une onde ppm, dans mon cas elles sont progressives selon z

J'ai donc E1 = A*cos(kz-wt) et E2 = A*cos(kz-wt+δ)
On a donc le champ résultant E = E1 + E2 = A(cos(kz-wt) + cos(kz-wt+δ))

En un point M fixé on est à z fixé donc on aurait E(M,t) = A (cos(-wt)+cos(-wt+δ))
En complexe E(M,t) = Aexp(-iwt) + Aexp(-iwt+iδ)
D'ou E(M,t) = (A+Aexp(+iδ))exp(-iwt)

Sachant I proportionnel à la moyenne quadratique de E on a I = K*( module de (A+Aexp(iδ)) )^2

or ( module de (A+Aexp(iδ)) )^2 = (A+Aexp(iδ)) * (A+Aexp(-iδ)) = 2*A^2 + A^2*(exp(iδ)+exp(-iδ))
Ce qui donne en réel : 2*A^2 + 2*A^2*cos(δ)

Donc I(M,t) = 2K * A^2 *(1+cos(δ)) = 4*K*I0 *(1+cos(δ))

Mais je ne me suis pas servi de la relation.

Pouvez vous me dire si mon raisonnement est bon et/ou le corriger à l'endroit où je me trompe/n'utilise pas la relation.

Je vous remercie par avance.

[LPFR]

Re.
Vous n’avez pas eu besoin d’additionner des cosinus car vous êtes passée directement en notation complexe (ce qui est nettement plus commode).
Mais comme on vous donne la relation, j’imagine qu’ils voulaient que vous le fassiez « à la dure » sans utiliser les complexes.
A+

[Tirlititi]

Du coup mon raisonnement est bon, le résultat final s'exprime avec un K dont on ne connait pas la valeur ?

J'essaye de le faire "à la dure" pour voir :

Je repars de E(M,t) = A (cos(-wt)+cos(-wt+δ))

Sachant I proportionnel à la moyenne quadratique de E on a I = < [A (cos(-wt)+cos(-wt+δ))]*[A (cos(-wt)+cos(-wt+δ))] >



Ce qui me donne



Et là je ne vois pas trop comment continuer ce qui est en -wt me gène.

[LPFR]

Re.
Faites la somme des cosinus d'abord et la moyenne quadratique ensuite.
A+

[Tirlititi]

Re,
J'essaye ci-dessous :
A(cos(kz-wt) + cos(kz-wt+δ))
= A(cos(kz)cos(wt)+sin(kz)sin(wt )+cos(kz-wt)cos(δ)-sin(kz-wt)sin(δ))
=A(cos(kz)cos(wt)+sin(kz)sin(w t)+cos(kz)cos(wt)cos(δ)+sin(kz )sin(wt)cos(δ)-sin(kz)cos(wt)sin(δ)+sin(wt)co s(kz)sin(δ))
=A(cos(kz)cos(wt)(1+cos(δ))+si n(kz)sin(wt)(1+cos(δ))-sin(kz)cos(wt)sin(δ)+sin(wt)co s(kz)sin(δ))
=A((1+cos(δ))(cos(kz)cos(wt)+s in(kz)sin(wt)+sin(δ)(cos(kz)si n(wt)-sin(kz)wos(wt))
=A((1+cos(δ))(cos(wt-kz))+sin(δ)(sin(wt-kz)))

Et je dois encore un peu simplifier je pense mais je bloque. Je n'ai pas l'impression d'avoir utilisé l'égalité fournie qui plus est.

[LPFR]

Re.
Vous faites l’inverse de ce qu’il faut faire. Il ne faut pas décomposer chaque cosinus en somme de fonctions, mais transformer la somme de cosinus en produit de fonctions.
Et la moyenne quadratique ne peux pas dépendre du temps. L’amplitude est constante.
A+

[Tirlititi]

Re,
Le problème est qu'avec cos(kz-wt) + cos(kz-wt+δ)
Je ne vois pas de a et de b qui me donnerait cos(a-b) + cos(a+b)

Bien à vous,

[LPFR]

Re.
Regardez ici:
https://fr.wikipedia.org/wiki/Identi...es_en_produits
A+

[Tirlititi]

Re,
Mais c'est le contraire de l'aide qui m'est donnée dans l'énoncé, je vais donc transformer une somme en produit non un produit en une somme. Ils mentionnent sur la page que vous m'avez donné a=p+q/2 et b=p-q/2, c'était l'astuce en plus à trouver tout seul ?

Donc sans tenir compte de z qui est fixe pour M fixé
cos(wt) + cos(wt+δ)
Je pose a=wt+δ/2 et b=-δ/2
Et j'obtiens le résultat : 2*cos(wt+δ/2)*cos(-δ/2)

Et en moyenne quadratique cela donnerait (cos(-δ/2))^2

Ca m'a l'air correct, à ceci près que je sais pas trop comment je le rédigerai.
Au fond, comment on sait dans les cos au début si on écrit cos(wt+δ/2) ou cos(wt-δ/2) quand on a la différence de marche ?

[LPFR]

...
Au fond, comment on sait dans les cos au début si on écrit cos(wt+δ/2) ou cos(wt-δ/2) quand on a la différence de marche ?

Re.
Ça dépend du chemin que vous prenez comme référence de chemin optique.
Dans l'énonce je pense qu'ils prennent la distance du rayon (inexistant) qui part du milieu entre les sources.
Mais tous les choix donnent le même résultat.
A+

[Tirlititi]

Re,
En effet avec la parité du cos.
Et pour "le résultat final s'exprime avec un K dont on ne connait pas la valeur, ce n'est pas grave ?"

[LPFR]

Re.
Je ne vois pas de quel K vous parlez.
Mais l’intensité des franges d’interférence dépend de l’éclairement des trous, de leur dimension et de plusieurs autres choses. Donc, il est normal que vous n’ayez le résultat qu’à un facteur près.
A+

[Tirlititi]

Re,
J'ai mis un K car on mentionne que les capteurs fournissent un signal proportionnel à l'intensité lumineuse.
Le K apparait dans les développements de calculs que je vous ai écrit.
Il ne devrait pas y être ?

[LPFR]

Re.
On s’en fout de K. Et il n’aurait pas du figurer dans vos calculs.
Ce qui compte est l’intensité lumineuse I.
Une fois que vous l’aurez calculée vous pourrez écrire que la tension des capteurs V = K.I
A+

Je ferme boutique pour ce soir.

[Tirlititi]

Re,
Je vous remercie pour votre réponse.
Et je vous remercie pour l'ensemble de l'aide que vous m'avez apportée aujourd'hui.

Bonne soirée à vous,