Calcul de Vs/Ve,en notation complexe

[invite9c5f7482]

Bonsoir,j'ai entamé cet exo,mais avant de poursuivre mes calculs,je voulais savoir si le début de mon raisonnement est bon s'il vous plait.
Voici l'énoncé suivit de mon raisonement.
2pi34.jpg.
2pi35.jpg
J'ai omis de préciser que Zeq'=Z1+Zeq=R+zeq.
-----

[phys4]

Mauvais début :
Vous n'avez pas le droit de remplacer

par

il faut appliquer les règles de calcul usuel.

[invite9c5f7482]

Bonsoir,je n'ai pas remplacer,c'est quand je calcul Yeq=1/Zeq que je passe aux inverse.

[phys4]

L'écriture complète est assez lourde.
Je vous conseille de calculer H en gardant Z1, Z2 et Z3 jusqu'au calcul final et de remplacer par leurs valeurs seulement après avoir simplifié.

A noter que je ne trouve pas le résultat proposé, mais un coefficient différent au dénominateur.
Je serais curieux de voir ce que vous trouvez.

[A voir en vidéo sur Futura]

[invite9c5f7482]

Bonsoir,je suis partie de Vs/Ve=zeq/(R+Zeq) d'ou Vs/ve=1/(1+R/Zeq) et je trouve au final(sauf erreur) vs/ve=(-(Lw)²+RjLw)/(R²+3jLwR)-(Lw)²).
Mais pas sûr que c'est ce qu'on demande,vous avez probablement raison.

[invite9c5f7482]

L'autre problème qui se pose c'est que dans mon cours je trouve que le "m" de l'expression qu'on dois trouvé vaut m=(R/2).racine(C/L). or le circuit qu'on a c'est du RL pas du RLC.

[phys4]

Ce n'est pas cet exercice, et dans le cas présent, m est un nombre sans dimension.

[invite9c5f7482]

Ok merci,ce que j'ai trouvé est ci-dessus,mais je vérifierai si c'est bien ça .

[invite9c5f7482]

Bonsoir,je dois calculer le module et l'argument de cette fonction de transfert,mais je n'ai pas bien compris comment calculer l'argument de H(jw);(H(jw) étant écrit tout en bas de la photo).
Quelqu'un peut-il m'aidé si possible?

Pour la n-ième fois, les images doivent être insérées comme pièces jointes.

Si il y a des erreur dans le module veillez me le dire svp.

[invite9c5f7482]

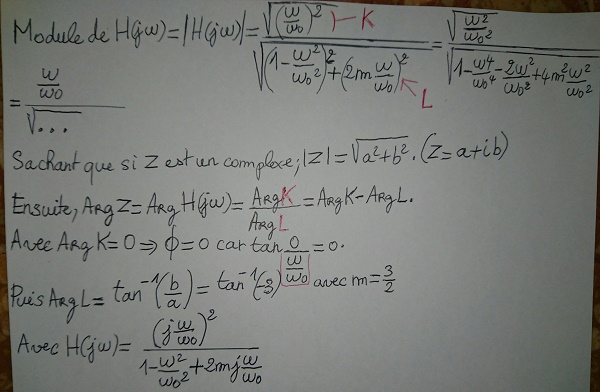
XXXX La critique de la modération doit se faire par messages privés, comme indiqué dans la charte XXXX

[phys4]

Je ne vois pas l’intérêt de créer de une nouvelle discussion pour traiter des réponses, et de la suite du problème ?

La valeur de m à trouver, est bien m = 3/2

[albanxiii]

Bonjour,

Je ne vois pas l’intérêt de créer de une nouvelle discussion pour traiter des réponses, et de la suite du problème ?

En effet, j'ai fusionné les deux discussions.

Pour la modération.

[phys4]

Pour la réponse concernant l'argument, vous pouvez écrire que l'argument d'un nombre est la différence entre l'argument du numérateur et l'argument du dénominateur.

Pour le résultat vous êtes encore loin : l'argument d'un réel négatif (numérateur) n'est pas zéro mais

L'argument du dénominateur ne se résume pas à un angle fixe, il varie entre et

[invite9c5f7482]

Pour la réponse concernant l'argument, vous pouvez écrire que l'argument d'un nombre est la différence entre l'argument du numérateur et l'argument du dénominateur.

Pour le résultat vous êtes encore loin : l'argument d'un réel négatif (numérateur) n'est pas zéro mais

L'argument du dénominateur ne se résume pas à un angle fixe, il varie entre et

Ok merci pour votre aide ,je ne savais pas que pour un réel négatif on avait toujours pi,bon à savoir.
Je vais revoir ça pour le dénominateur.
je suppose que mon module est bon(quoique j'aurai pas dû dévelloper le bas).

[stefjm]

Ok merci pour votre aide ,je ne savais pas que pour un réel négatif on avait toujours pi,bon à savoir.

Dessinez la représentation de -1 dans le plan complexe et vous verrez bien combien vaut l'argument.
Certains auteurs préfèrent -pi, plutôt que pi.

[invite9c5f7482]

Dessinez la représentation de -1 dans le plan complexe et vous verrez bien combien vaut l'argument.
Certains auteurs préfèrent -pi, plutôt que pi.

Effectivement c'est ça!

[invite9c5f7482]

Pour la réponse concernant l'argument, vous pouvez écrire que l'argument d'un nombre est la différence entre l'argument du numérateur et l'argument du dénominateur.

Pour le résultat vous êtes encore loin : l'argument d'un réel négatif (numérateur) n'est pas zéro mais

Bonjour phys4,alors pour le dénominateur c'était effectivement pas bon,pour mon dénominateur on peut dire que Arg(K)=Arg(-w²/w0)+Arg(3w/w0)=pi+Arg(3w/w0) avec m=3/2 donc 2m=3.

[phys4]

Pour le dénominateur il faut prendre l'expression complète.
Je vous invite à revoir la définition et comment s'exprime l'argument pour un complexe quelconque.

Une bonne astuce serait de supprimer le numérateur en écrivant


ainsi il n'existe plus qu'un seul terme.