Bonjour à toutes et tous,
Je suis en train de lire le tome 1 (en français) de Mécanique du renommé Richard Feynman.
Je suppose que nombre de gens ici en ont au moins entendu parler, sinon sûrement lu.
Dans le chapitre 4 sur la conservation de l'énergie, paragraphe 4.2 sur l'énergie potentielle gravitationnelle, j'ai du mal à comprendre le raisonnement de Feynman pour démontrer l'impossibilité d'un mouvement perpétuel.
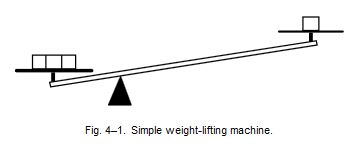
Feynman utilise l'exemple de machines à soulever des poids comme celle-ci:
Pour illustrer cela, voici ce que Feynman explique :Si nous avons soulevé et abaissé un certain nombre de poids et ramené la machine à sa situation initiale, nous trouvons que le résultat total est d'avoir levé un poids, alors nous avons une machine à mouvement perpétuel, car nous pouvons utiliser ce poids pour faire fonctionner quelque chose d'autre. C'est dire qu'il faut que la machine soit ramenée à sa situation initiale exacte, et de plus qu'elle soit un système complètement clos - qu'elle n'ait pas reçu de l'énergie pour soulever ce poids d'une certaine source extérieure
On considère une machine (cf schéma ci-dessus) qui soulève des poids de trois unités à l'aide d'un poids d'une unité. Pour faire fonctionner la machine de manière effective (je comprends "dans la vraie vie", avec frottements & co.) il faut soit enlever un peu de masse des trois unités de poids pour soulever le plateau de droite, soit rajouter un peu de poids sur le plateau de droite pour soulever les trois poids de gauche. Ceci illustre qu'on a besoin d'apporter un peu plus d'énergie dans la vraie vie, je pense notamment pour compenser les frottements avec la liaison etc... Il dit de plus que :
On est d'accord que même une machine idéale, que j'entends moi sans aucune perte de type frottements, nécéssite quand même un léger déséquilibre de poids d'un côté ou de l'autre pour fonctionner ? sinon la machine ne lèverait rien mais serait avec les deux plateaux à l'horizontal ?Les machines idéales, bien qu'elles n'existent pas, ne nécessitent rien de plus
De plus, prise de manière isolée, on est d'accord qu'une telle machine ne reviendrait pas à son état initial toute seule, donc pas de mouvement perpétuel avec une machine seule telle quelle ?
Ensuite, venons à la démonstration elle-même visant à démontrer que le mouvement perpétuel n'existe pas:
Voici mes interrogations :On suppose qu'il existe une machine réversible (machine A), qui abaisse une unité de poids d'une unité de distance, et en même temps soulève trois unités de poids d'une distance X. Supposons également une machine B, pas nécéssairement réversible, qui abaisse un poids d'une unité de distance, mais qui soulève trois poids d'une distance Y. Nous pouvons prouver que Y n'est pas plus grand que X, c'est à dire qu'il est impossible de construire une machine qui soulève un poids d'un hauteur plus élevée que celle à laquelle il sera soulevé par une machine réversible.
Supposons que Y>X. Nous prenons un poids d'une unité et nous l'abaissons d'une unité de hauteur avec la machine B, et celle-ci soulève le poids de 3 unités d'une hauteur Y. Alors nous pouvons descendre le poids de Y à X, produisant de l'énergie disponible, puis nous utilisons la machine réversible A en sens inverse pour abaisser le poids de trois unités sur une distance X et lever le poids d'une unité d'une unité de hauteur. Ceci ramènera le poids d'une unité à sa position initiale, et laissera les deux machines prêtes à être utilisées à nouveau ! Si Y est plus grand que X, nous aurions donc un mouvement perpétuel, ce que nous avons supposé impossible.
Ce que je comprends c'est que la machine B peut soulever trois unités de poids d'une distance Y en abaissant l’unité de poids, d'une unité de hauteur. Si on abaisse le poids de trois jusqu'à X<Y, alors le poids unitaire sera abaissé d'une distance inférieure à l'unité. Si maintenant on place à gauche de cette machine B la machine A de manière à abaisser le poids de trois (qui est sur la machine B, je suppose) de X, il faut que la machine A soulève son plateau droit de moins d'une unité de hauteur. Alors que Feynman parle d'abaisser le poids de 3 de X et de lever le poids unitaire d'une unité... Déjà là il y a quelque chose que je ne comprends pas ! en tout cas dans la manière dont je me suis imaginé en schéma son explication.
De plus il conclut sur "on revient donc à l'état initial. Et si Y>X, chouette on aurait un mouvement perpétuel, ce qui est impossible, donc une machine réelle soulève moins haut qu'une machine réversible.
Je n'ai toujours pas saisi la notion de mouvement perpétuel qui pour moi est un mouvement qui par définition ne s'arretrait jamais, car ne perdrait aucune énergie par frottements d'une quelconque nature. Mais pour cela, il faudrait un mouvement périodique, où il y a un transfert d'énergie constant entre deux entités par exemple. Alors que dans l'explication de R. Feynman, je ne retrouve que la notion de retourner à son état initial en ayant fait un mouvement sans avoir travaillé pour autre chose que ce mouvement (sans perdre par frottement). mais pour moi revenir à son état initial ne signifie pas qu'il y a de l'énergie pour réitérer le mouvement à l'infini, du coup la manière dont je comprends sa définition ne me convainc pas.
Quelqu'un pourrait-il m'éclairer sur ces questions ? Peut-être que j'ai une mauvaise schématisation dans ma tête de où sont placés les poids, les machines etc.
Pour ce qui voudraient avoir le texte intégral, le cours de Feynman est en libre accès sur internet en anglais:
http://www.feynmanlectures.caltech.edu/I_04.html
Merci d'avance et bon weekend,
tibmaster
-----





 mais pas facile de se représenter la réalité avec le modèle quantique.
mais pas facile de se représenter la réalité avec le modèle quantique.