Théorème d'Ampère, direction du champs

[mronyme]

Bonjour,
je suis actuellement entrain de retravailler le théorème d'Ampère ( je passe des rattrapages fin août ), et j'avais une question concernant la direction du champs.
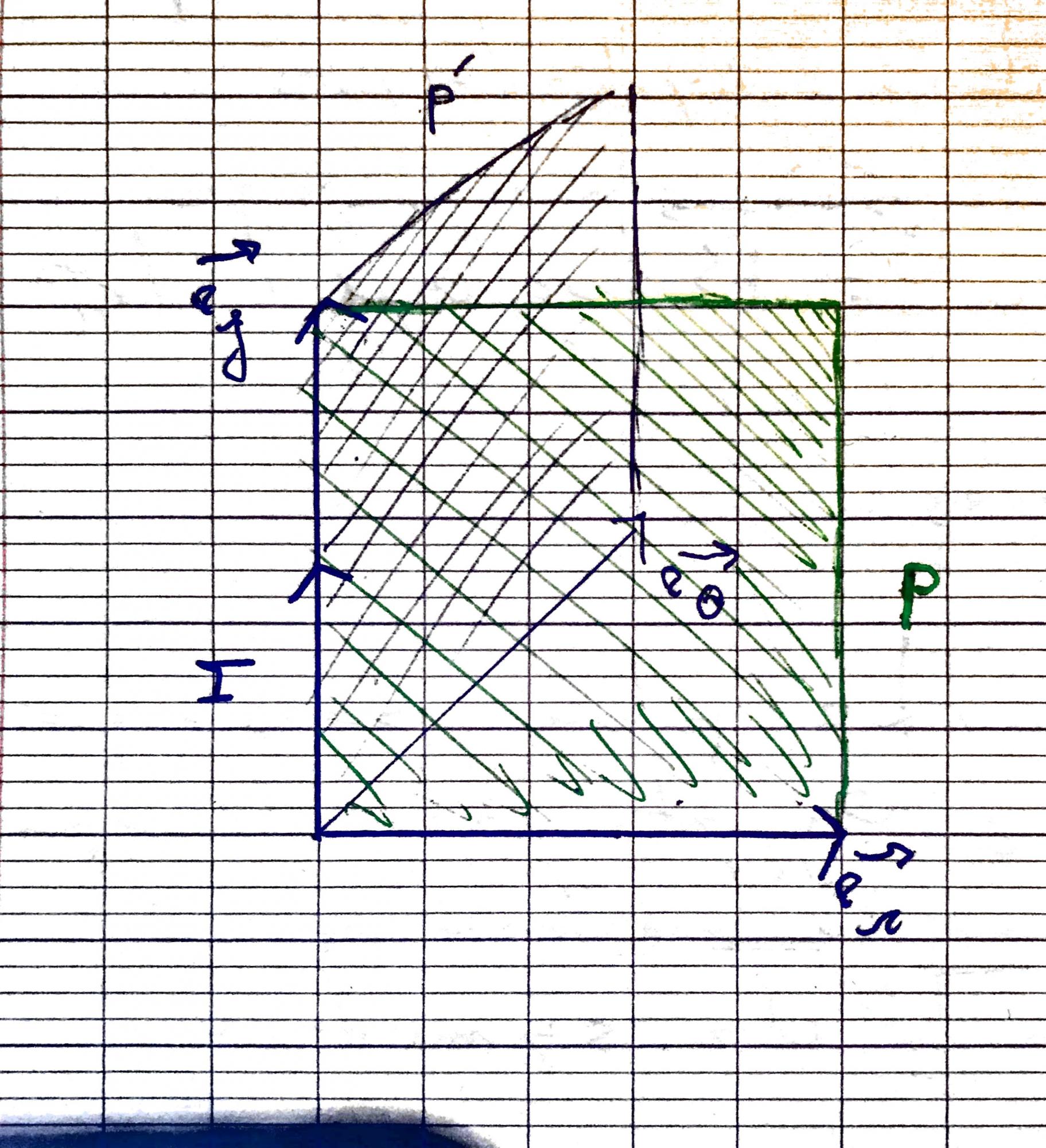
Prenons le cas canonique d'un fil infini, avec le courant orienté vers le haut.
On se place en coordonnées cylindriques (er,e0,ez). On sait que le champs B ( magnétostatique ) est perpendiculaire au plan de symétrie du courant passant par M.
Or pour moi il y a deux plans de symétrie, P(M,Er,ez) et P'(M,e0,ez) le champs pourrait donc être selon e0 ou eR, or dans tous les exercices ont indique qu'il est selon e0, pourquoi ? Je bloque sur cette question qui me paraît primordiale depuis un certains temps déjà, HELP !
Merci d'avance, n'hésitez pas à me demander des précisions.
-----

[coussin]

Le plan P' n'est pas un plan de symétrie. J'ai du mal à visualiser ce plan comme vous le définissez d'ailleurs mais j'imagine que vous voulez dire un plan horizontal, non ?
Les seuls plans de symétrie sont ceux contenant le fil. La direction perpendiculaire à ces plans est eTheta.

[LPFR]

Bonjour et bienvenu au forum.
Comme règle générale, des qu’on est dans le champ magnétique, le principe de Curie n’est pas applicable. Par exemple, un fil infini a des plans de symétrie qui contiennent le fil. Mais ces plans ne sont pas des plans de symétrie du champ magnétique. Certains on essayé de sauver le principe de Curie en disant que le champ magnétique n’est pas un vecteur pais un pseudo-vecteur. Grand bien leur fasse.

De même, la symétrie n’empêcherai pas le champ dans cet exemple d’avoir une composante radiale. Le seul moyen que je connais de réfuter le champ radial est de faire appel à l’équation de Maxwell div B = 0.

Donc, je vous conseille de ne pas utiliser la symétrie sans des infinies précautions dans ce type de problème.
Au revoir.

[mronyme]

Merci pour vos réponses rapides, je tente un schéma en perspective pour essayer d'être plus clair :


J'ai représenté le fil infini qui est selon ez, et les deux plans ( verticaux ) P(er,ez) et P'(e0,ez)
A mon sens un plan horizontal, c'est à dire selon les vecteurs er et e0(Theta), est plan d'antysimétrie du courant. (Et donc le champs B lui appartient )
J'espère avoir été clair

[A voir en vidéo sur Futura]

[coussin]

Oui et donc...
B appartient au plan horizontal (antisymétrie : composante ez nulle) et doit être perpendiculaire aux plans de symétrie verticaux (doit être suivant eTheta).
L'argument des plans de symétrie est suffisant pour déterminer complètement B. L'argument du plan d'antisymétrie n'est pas nécessaire en fait...

[mronyme]

Si P' est bien un plan de symétrie du courant, je ne vois pas pourquoi le champs ne pourrait pas être selon er, puisque ( sauf erreur de ma part ) le vecteur er est bien orthogonal au plan P', plan qui est défini par les vecteurs ez et eTheta comme sur ma figure ci dessus.

Oui effectivement le plan d'antisymétrie sert juste à confirmer le résultat.

[coussin]

Le plan défini par ez et eTheta n'est pas un plan de symétrie ni d'antisymétrie... Sauf si le point M est sur le fil au quel cas le système de coordonnées est mal défini...

[mronyme]

J'avoue être un peu perdu, pourquoi le plan défini par ez et eTheta n'est ni plan de symétrie ni d'antisymétrie ? ( à quoi correspond t'il alors ? ). Désolé ça fait bcp de question mais je cherche vraiment à comprendre un point du cours qui me paraît bien ambigüe.
Je considère que le point M est situé n'importe où, sauf sur le fil.
Pour moi les lignes de courant sont contenues aussi bien dans P que P'. J'ai peut être omis de préciser que je considère que le fil est un cylindre (Il n'est pas en 2D).

[coussin]

Je comprends en voyant votre dessin : votre système de coordonnées est faux. Les vecteurs unitaires er, eTheta et ez doivent être centrés à la position du point M. Ce que vous avez dessiné est en fait un système de coordonnées cartésien...

http://mathworld.wolfram.com/Cylindr...ordinates.html

[mronyme]

Merci bcp ! Je viens de comprend d’où venais mon soucis de compréhension, je confonds cartésien 3D et cylindrique.
Encore merci ! Bonne soirée à vous.