Kruskal and co

[mach3]

S'il s'agit de la singularité r=0, c'est à dire T²-X²=1 en coordonnées de KS, c'est un volume.

Pour la taille, je n'en sais rien. En coordonnées de KS comme en coordonnées de Schw. région II, ses coordonnées (X, Θ, φ) sont celles d'un cylindre sphérique infini (X couvre tout le droite réelle). Faudrait calculer le volume propre. Possible qu'il tendre vers 0.

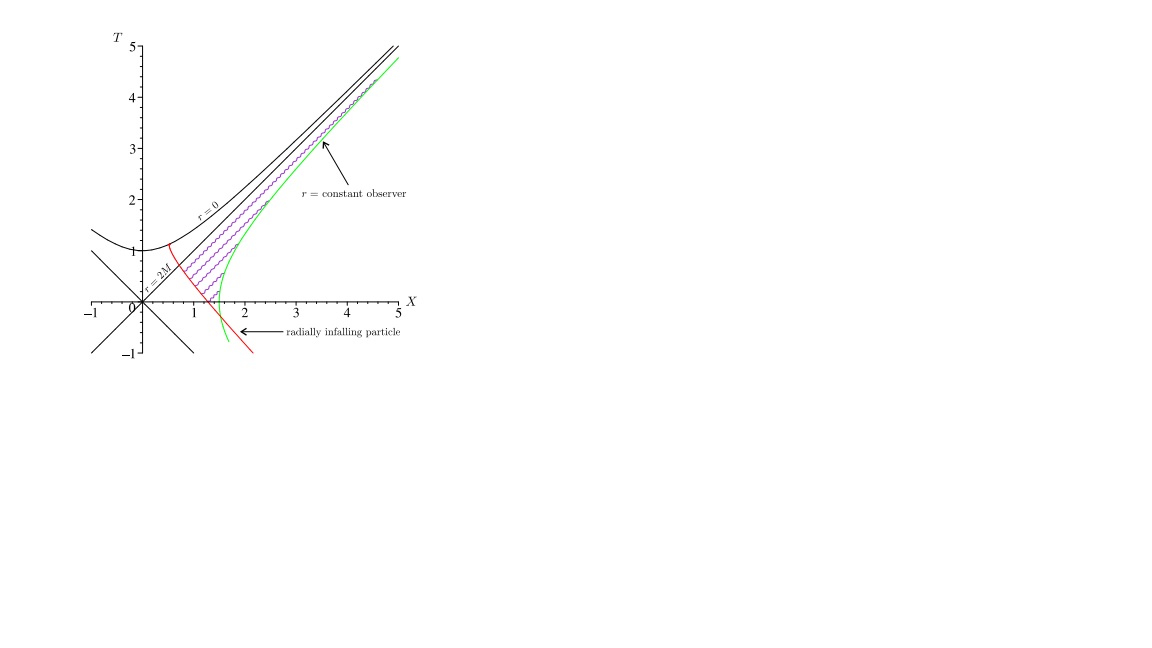
La dernière fois que nous avions évoqué le sujet, j'avais été convaincu qu'il s'agissait d'une ligne de genre espace (tel l'axe z des coordonnées cylindriques euclidiennes, avec les coordonnées angulaire dégénérées) alors que je pensais qu'il s'agissait d'un volume. Quels arguments ou réflexions pour expliquer ce revirement?

m@ch3
-----

[Amanuensis]

En gros je mélange limite de la forme et forme de la limite, désolé pour le manque de clarté.

Comme la variété est sans bord, la notion de la forme de la singularité n'est pas très claire en fait. Ce qui est sûr, c'est qu'on s'intéresse à des volumes (des cylindres sphériques) «inclus les uns dans les autres», et qu'on voudrait parler de la limite. En topologie sans métrique, cela peut être aussi bien une surface, qu'une ligne ou un point, et même d'autres trucs.

Les considérations métriques semble pointer vers une ligne.

Une ligne limite d'une série de cylindres sphériques.

(Maintenant, il n'y pas de «ligne» représentant la singularité dans la variété elle-même, seulement des volumes l'approchant.)

Donc

S'il s'agit de la singularité r=0, c'est à dire T²-X²=1 en coordonnées de KS, c'est un volume.

est mal dit, au mieux. J'ai été entraîné par le fait que la question portait sur la taille, et là faut s'intéresser aux volumes dont c'est la limite.

[mach3]

Ok. La difficulté c'est donc qu'on parle de la forme d'un truc qui ne fait pas partie de la variété. Au mieux on peut dire que c'est contenu dans un cylindre sphérique arbitrairement petit.
J'avais pensé à une autre formulation de la question, est-ce que 2 particules, partant en chute libre sans vitesse coordonnée initiale (de Schwarzschild) des mêmes coordonnées r et t mais de coordonnées angulaires différentes, aboutissent au même "événement final"?

m@ch3

[Amanuensis]

Pas un même événement dans la variété. Mais intuitivement même limite sur la singularité, par symétrie.

Les différentes limites sur la singularités correspondent à des instants de départ (en Schw.) différents.

[viiksu]

Une ligne limite d'une série de cylindres sphériques.

'est la tête qu'aurait la singularité si on avait le temps de l'approcher? Une ligne sans épaisseur et infinie?

[viiksu]

J'avais pensé à une autre formulation de la question, est-ce que 2 particules, partant en chute libre sans vitesse coordonnée initiale (de Schwarzschild) des mêmes coordonnées r et t mais de coordonnées angulaires différentes, aboutissent au même "événement final"?

m@ch3

Question conjointe quelle est la trajectoire d'un solide tombant sans vitesse initiale depuis un rayon r dans un KS est-ce la tangente à l’hyperbole?

[Amanuensis]

'est la tête qu'aurait la singularité si on avait le temps de l'approcher? Une ligne sans épaisseur et infinie?

Pourrait être ça. C'est ce qu'on trouve avec les coordonnées de KS (ou celle de Schw. région II) sous certaines hypothèses.

Mais comme dit précédemment, la notion de forme d'une limite demanderait à être clarifiée du point de vue mathématique.

---

Quant au volume propre limite, quelques tentatives de calcul que j'ai faites arrivent toutes à la même chose: indéterminé, un produit d'un 0 et d'un infini, les deux facteurs semblant indépendants l'un de l'autre (limite quand r tend vers 0 pour l'un, et quand X tend vers l'infini pour l'autre). Le volume des cylindres sphériques est infini (produit de r² non nul par un infini).

[mach3]

Question conjointe quelle est la trajectoire d'un solide tombant sans vitesse initiale depuis un rayon r dans un KS est-ce la tangente à l’hyperbole?

c'est, il me semble, traité dans la discussion que j'ai mis en lien dans le message 131.

m@ch3

[mach3]

'est la tête qu'aurait la singularité si on avait le temps de l'approcher? Une ligne sans épaisseur et infinie?

c'est la tête qu'a, vraisemblablement, la singularité dans la solution de Schwarzschild. Par contre, si je comprends ce qui est peut-être sous-entendu, on ne peut pas voir (au sens avec ses yeux) la tête de la singularité, même si on avait le temps de s'en approcher.

m@ch3

[viiksu]

Et alors pour le TN de Kerr on dit que la singularité a la forme d'un anneau ou d'un tore et qu'on peut même passer au travers, alors info ou intox?

[Amanuensis]

Je ne me suis jamais coltiné les maths.

Je remarque juste qu'on voit la même chose qu'en Schw. : l'usage des coordonnées extérieures pour traiter de l'intérieur, malgré le changement de signe de g^tt. Ce changement implique que t est alors une coordonnée spatiale, et qu'une autre des coordonnées est devenue temporelle (a priori c'est r).

Dans la figure https://en.wikipedia.org/wiki/File:S...Black_Hole.jpg la singularité est décrite comme x²+y²=a² et z=0, ce qui ne décrit pas un anneau spatial si les coordonnées ne sont pas toutes spatiales.

D'ailleurs le cas limite a=0 (TN sans rotation) donne r=0, ce qui ne décrit pas un lieu en géométrie de Schw., ce qui a été répété plusieurs fois.

Cela semble le pendant de dire que la singularité dans la géométrie de Schw. est un point spatial...

[viiksu]

Donc c'est faux a priori?

[Amanuensis]

Donc c'est faux a priori?

Je n'en sais rien. En tout cas, je ne véhiculerai pas cette description.

[viiksu]

Il me semble que vous faites une distinction entre la variété mathématique théorique à quatre dimensions et la relativité générale, n'est-ce pas une variété "pure" . Le fait que le temps soit la quatrième dimension en RG est-ce que cela change quelque chose ? Je suppose que dans une variété mathématique les 4 dimensions sont équivalentes?

Ensuite on nous parle de singularité en anneau pour un objet qui a priori est hors du champ théorique de la RG, donc inconnaissable avec elle.

[mach3]

Il me semble que vous faites une distinction entre la variété mathématique théorique à quatre dimensions et la relativité générale, n'est-ce pas une variété "pure" . Le fait que le temps soit la quatrième dimension en RG est-ce que cela change quelque chose ? Je suppose que dans une variété mathématique les 4 dimensions sont équivalentes?

Il y a les variétés riemanniennes, où localement la métrique est euclidienne, c'est à dire que c'est une forme définie positive (le tangent à la variété est un espace euclidien et les vecteurs non nuls sont tous de carré scalaire strictement positifs), et les variétés pseudo-riemmanniennes, où localement la métrique n'est pas euclidienne (pas définie positive, c'est à dire que des vecteurs non nuls du tangent ont un carré scalaire nul ou négatif). Parmi ces dernières, on a les variétés minkowskiennes, qui ont 4 dimensions, et où l'espace tangent est l'espace-temps de Minkowski, où on peut trouver (en convention -+++) des sous-espaces à 3 dimensions qui sont euclidiens (vecteurs non nuls de carré strictement positifs) et dont les orthogonaux à 1 dimensions sont peuplés de vecteurs dont le carré est négatif. Dans cet espace l'ensemble des vecteurs non nuls de carré nul (dit de genre nul) forment un cône "sphérique" (connait pas le bon terme, c'est l'analogue du cylindre sphérique, mais pour le cône), souvent appelé cône de lumière, séparant les vecteurs de carré positif (genre espace) et les vecteurs de carré négatif (genre temps).
Les variétés riemanniennes et pseudoriemanniennes (dont les minkowskiennes) ont beaucoup en commun (même notions de connexion, de géodésiques, de courbure) mais les propriétés géométriques sont différentes. Cela est hérité du fait que la géométrie euclidienne est différente de la géométrie de Minkowski (par exemple, pas d'inégalité triangulaire en général, existence d'angles hyperboliques, etc).

Ensuite on nous parle de singularité en anneau pour un objet qui a priori est hors du champ théorique de la RG, donc inconnaissable avec elle.

La forme en anneau sort des équations qui elles-mêmes sortent de la RG. Après, tout comme la singularité d'un trou noir de Schwarzschild, cette singularité est en dehors de l'ouvert (c'est sa limite si j'ai bien capté les dernières explications d'Amanuensis), donc d'une certaine manière non incluse...

m@ch3

[Amanuensis]

Il me semble que vous faites une distinction entre la variété mathématique théorique à quatre dimensions et la relativité générale

Il y a toujours une distinction entre les maths et la physique, non? En quoi la RG serait particulière?

Le fait que le temps soit la quatrième dimension en RG est-ce que cela change quelque chose ?

Que le temps soit une dimension n'a pas grand sens en RG. Comme l'explique Mach3, en RR et RG la distinction temps/espace s'exprime autrement, à partir de la métrique et de la classification des vecteurs en genre.

Et changer quelque chose à quoi?

Je suppose que dans une variété mathématique les 4 dimensions sont équivalentes?

Non. Avec une métrique minkowskienne il y a trois genres distincts pour les vecteurs, les directions (les "dimensions") ne sont pas toutes interchangeables comme en géométrie euclidienne.

Ensuite on nous parle de singularité en anneau pour un objet qui a priori est hors du champ théorique de la RG, donc inconnaissable avec elle.

Il y a les maths qu'il faut pour traiter des singularités, c'est juste moins simple que les figures géométriques du plan euclidien.

(Et les remarques que j'ai faites ne portent pas seulement sur la singularité mais de tout le traitement de l'intérieur.)

----

Dans toutes ces remarques on sent une difficulté quant à l'articulation entre maths et physique.

[Amanuensis]

comme en géométrie euclidienne.

Lire "comme en géométrie du plan euclidien".

Pour réfléchir sur l'idée "d'équivalence des dimensions", essayer de l'appliquer sur le tore euclidien (une surface, i.e., une variété de dimension 2, munie d'une structure différentielle et d'une métrique).

[viiksu]

Ci-joint si ça marche une trajectoire en chute libre dans KS.

[Mailou75]

Celui ci a l'air juste : particule tombant depuis l'infini spatial, située à environ r=1,4Rs à t=0, atteignant la singularité r=0 à t=Rs/c et vue par un observateur à environ r=1,5Rs constant. Il n'y a pas le temps propre de la particule ni celui de l'observateur, le graph ne donne donc pas d'info sur le redshift perçu malgré ce que laissent supposer les trajectoires lumineuses. Elles montrent toutefois que rien ne sera perçu au delà de l'horizon.

[Amanuensis]

C'est qualitativement ça. Maintenant, comme déjà écrit, la fonction exacte demande calculs. Sauf à tout vérifier en détail, pas de raison de penser que ce ne soit pas correct.

(Perso je n'utilise pas «trajectoire», mais plutôt «mouvement» ; on parle aussi d'équation horaire au lycée.)

[mach3]

Pièce jointe 349446

Ci-joint si ça marche une trajectoire en chute libre dans KS.

sinon, dans le fil cité par moi-même plus haut, il y a ça :
http://forums.futura-sciences.com/at...futura-253.jpg
ou ça :
http://forums.futura-sciences.com/at...futura-254.jpg
ou encore ça :
http://forums.futura-sciences.com/at...futura-255.jpg

mais bon, j'ai l'habitude de voir certain de mes messages totalement ignorés...

m@ch3

[viiksu]

mais bon, j'ai l'habitude de voir certain de mes messages totalement ignorés...

m@ch3

Mais non ce n'est pas ça c'est que la recherche des fils anciens n'est pas simple.

[Amanuensis]

Je suis curieux de savoir ce que vous tirez du tracé d'une ligne d'univers de chute libre. En particulier par rapport aux tracés des autres chutes.

[viiksu]

Ben c'est la chute de base, non?

[Amanuensis]

Cela ne répond pas à la curiosité indiquée...