Analyse Harmonique marée

[X1977]

Salut,
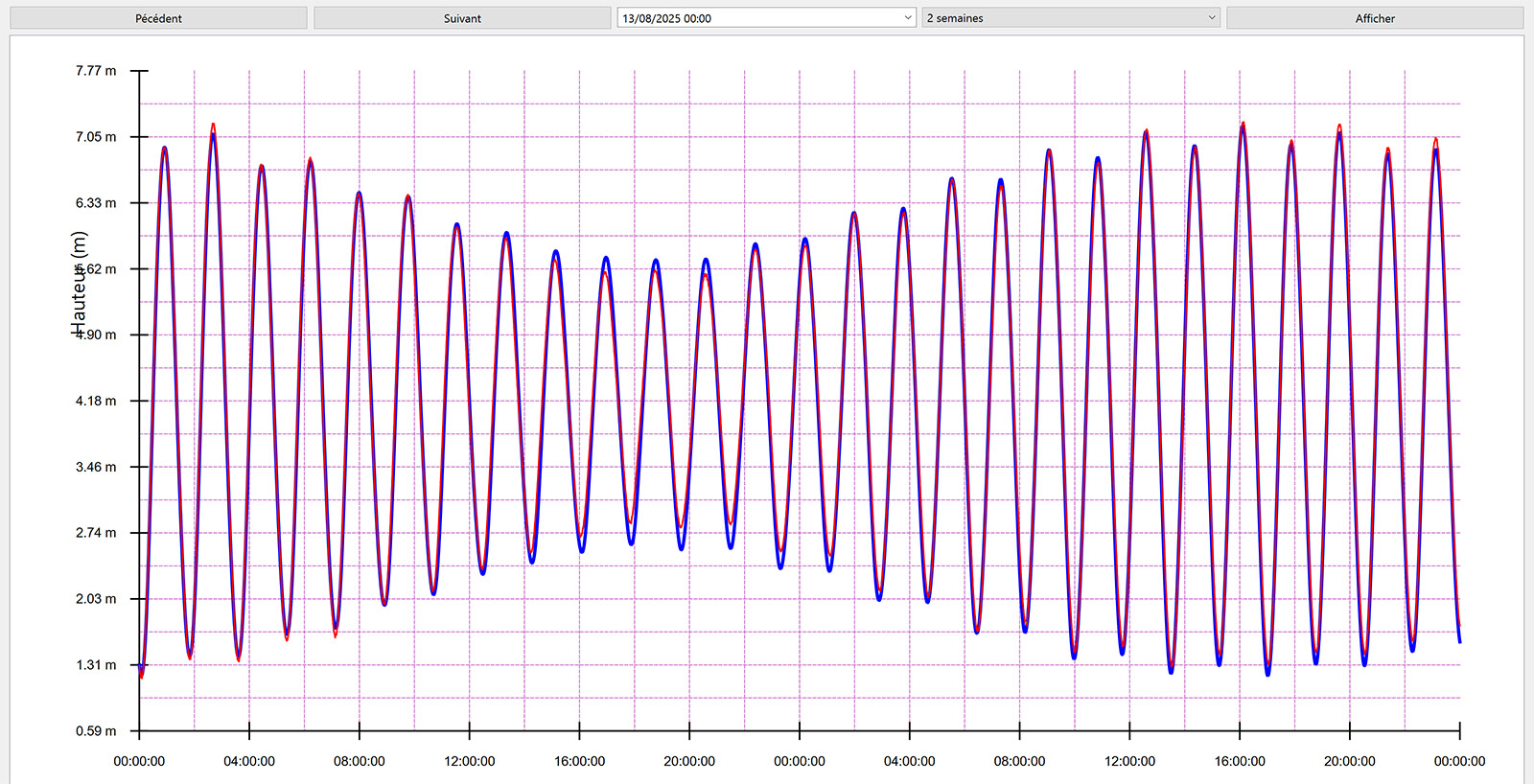
Je suis actuellement en train d’essayer de monter un petit programme Python qui me calculerait la hauteur d’eau suite aux marées à Brest.
Pour cela, j’utilise une forme harmonique, comme proposée par le site S.H.O.M (http://www.shom.fr/les-activites/act...sant-la-maree/) .
Toutefois, j’ai un petit problème :
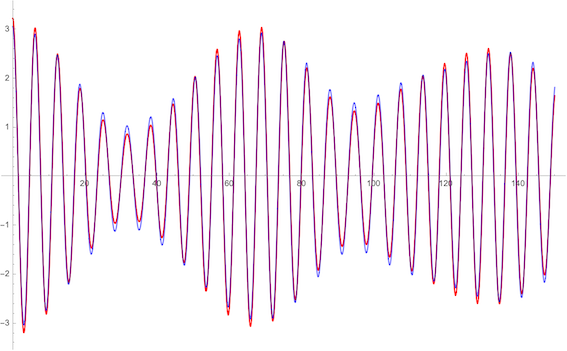
En utilisant les composantes les plus importantes (soit M2, S2, K1, O1, N2, P1), j’arrive à une somme d’amplitude environ égale à 2.5. Cela signifie qu’au maximum la hauteur d’eau sera de 2.5m au-dessus de la hauteur moyenne. Or, des marées peuvent parfois monter à près de 4M au-dessus de ce niveau moyen (21 Mars 2015 par exemple si vous voulez voir).

Auriez-vous une explication à proposer à cette différence ? Je sais que j’ai négligé pas mal d’harmonique mais je ne pense pas pouvoir combler la différence juste avec ça

En vous remerciant
-----

[phys4]

Dans ce logiciel, le résultat est par rapport au niveau moyen, qui n'est pas celui donné sur les cartes marines, car ces dernières se basent sur le niveau minimum.

Quand vous avez l'amplitude de 2,5 m, il faudra *2 pour avoir le marnage soit 5m, ce qui correspond à Brest !

Si vous voulez retrouver votre annuaire de marée local, il faut effectuer l'addition amplitude actuelle + niveau moyen.

[X1977]

Je comprends que dans les cas "classiques", une amplitude de 2.5 est suffisant ( on va d'une hauteur de 1.5 m à 6.5m au dessus du 0 hydrographique ) car le niveau moyen est d'environ 4m à Brest

Toutefois, cela interdit toute possibilité de hauteur d'eau au dessus de 6,5m ou en dessous de 1.5m ( ce qui est notamment le cas aujourd'hui !)

Auriez-vous une idée de comment dépasser cette limite ?
Je suis notamment tombé sur ce qu'il appelle un "terme constant", d'amplitude assez importante ( 0.8 environ) mais je ne comprends pas son utilité, étant donné que l'on a déjà une hauteur moyenne qui est utilisé .

[X1977]

Petit up
J'ai réussi en grande partie à retrouver les infos mais un soucis demeure.

La formule harmonique est de la forme Somme (cos(wt+phi) avec w la vitesse angulaire en degré/heure.
Je ne vois pas quelle caractéristique attribuer à t. Il est en h pour ne pas avoir de problème d'homogénéité mais si je mets simplement t=heure actuelle, alors la fonction est 24h périodique ce qui n'est absolument pas le cas des marées.
Une idée de quoi mettre ?
En vous remerciant

[A voir en vidéo sur Futura]

[phys4]

Vous devez avoir plusieurs composantes : le fondamental à une période de 12h 25, mais il des harmoniques et sous harmoniques en particulier une fréquence moitié qui correspond à 24h 50

Amusez vous bien.

[X1977]

Je comprends, mais tout ceci sont des constantes et on a une fonction h(t) où t est la variable .

Et je ne vois pas concrètement ce que ce t représente puisque si je mets simplement l'heure, j'ai une fonction qui ne dépend que de l'heure et non de la date, , ce qui ne représente absolument pas le phénomène des marées. Est- ce que t représente le nombre d'heures depuis une date t=0, une unité horaire propre au domaine des marées ...

Pour le reste, le tableau est fait et prêt à être utilisé avec les différentes composantes, leurs vitesses angulaires et leur phases mais qui sont tous des constantes .

[petitmousse49]

Bonjour
J'interviens peut-être un peu tard...
As-tu lu l'article suivant du shom : http://www.shom.fr/les-activites/act.../special-tipe/ ?
Tu peux y télécharger un fichier "formulation.zip" où les calculs sont très bien détaillés. J'ai eu la curiosité (et la patience !) de créer un petit programme sous Matlab reprenant pas à pas les calculs proposés. Les résultats que j'obtiens sont exactement ceux que proposent les applications gratuites pour téléphones portables (Marées...). Ces résultats diffèrent de quelques minutes parfois de ceux publiés annuellement par le shom, ce qui me parait logique dans la mesure où le shom ne rend pas public la totalité des composantes prises en compte ni les dernières mises à jour.

[X1977]

Salut

Merci de ta réponse
J'ai effectivement trouvé ce dossier fort intéressant et décidé d'en faire un programme et les résultats sont très satisfaisants !

Par simple curiosité , combien d'harmoniques as-tu utilisé ?
L'objectif derrière mon travail est de créer un bon compromis entre complexité du système et précision des résultats .

J'en ai personnellement utilisé 6 et c'était pour voir si ta meilleure précision est dû à des choix plus appropriés d'harmoniques ou une plus vaste sélection .

[petitmousse49]

Bonjour
J'ai pris en compte tous les termes explicités sur le fichier dont je t'ai fourni les références et j'obtiens, à la minute près, les valeurs fournies par l'application gratuite "Marée" de mon téléphone portable. J'y vois plus qu'une coïncidence ! Ces résultats peuvent différer de quelques minutes (pas plus de trois) des valeurs officielles fournies par le shom. Des termes, d'amplitudes a priori très faibles, peuvent avoir une influence non négligeables si, à certaines dates, ils se interviennent en phase. Puisqu'il s'agit juste de quelques minutes supplémentaires de copie sous MATLAB, autant garder tous les termes disponibles !

[X1977]

Les temps sont du même ordre chez moi mais les amplitudes varient plus pour les raisons que tu cites ( cela se voit notamment en testant le 21 Mars 2015 , ou une marée à coefficient 119 se produit) .

Toutefois, je travaille avec un modèle très simplifié ( système isolé Terre Lune Soleil) et donc je préfère avoir ces quelques variations et un modèle très simple au niveau des harmoniques !

Merci beaucoup en tout cas de ton aide

[CocoTyla]

Bonjour,
Je me permet de déterrer ce sujet. J'ai moi aussi tenté d'écrire un programme pour prévoir les marées à l'aide du dossier du SHOM mais malheureusement je bloque. Je n'y arrive pas et je ne sais pas comment faire. Je m'interresse pour l'instant simplement à la prévision de la hauteur d'eau à un instant donné. J'ai l'impression que mon souci vient du fait des conversions en radian ou degré de mes valeurs et aussi les termes en mètres ou en millimètres... Enfin je suis un peu dans le flou, sachant que vous l'avez fait, je serai ravi de bénéficier de votre aide.
En vous remerciant

[petitmousse49]

Bonjour
L’existence d'années bissextiles fait que le calcul de la durée entre deux dates n'est pas si simple qu'il n'en a l'air. Ce calcul conduit à la formule (4), l'origine des dates étant choisie arbitrairement au 1 janvier 1980 à 0h. Petite précision sur l'heure notée "t" dans la formule. Pour faire simple : c'est en très bonne approximation l'heure solaire à Greenwich (heure légale en France moins une heure l'hiver, moins deux heures l'été) à laquelle il faut retrancher une correction due à la longitude. Il faut retrancher (L*24/360) si L est la longitude mesurée en degrés. Ayant ainsi T, tu calcules, mesurés en degrés, les paramètres astronomiques qui permettent de situer sensiblement la lune et le soleil par rapport à la terre ( j'essaie de faire simple) :
s : longitude moyenne de la lune en degrés
h : longitude moyenne du soleil en degrés
p : longitude moyenne du périgée lunaire
N' : opposé de la longitude moyenne du nœud ascendant de la lune en degrés
p1 : longitude moyenne du périhélie
Il faut ensuite entrer les différents coefficients de la somme (1) du document et cela prend du temps. Attention dans les calculs de cosinus : toutes les données correspondent à des angles exprimés en degrés alors que certains logiciels de calculs n'acceptent que les radians...

[Lomiop]

Bonjour.

Je remonte le sujet, car tout comme l'auteur, je conçois un programme pour calculer la hauteur d'eau d'un port donné, dans le cadre de mon TIPE. Cependant, j'ai constaté (et le SHOM m'a confirmé) que le service d'aide aux TIPE n'était plus disponible suite aux changements du site. En effet le lien https://www.shom.fr/les-activites/ac.../special-tipe/ renvoie à une page non trouvée.
J'ai cependant trouvé des documents du SHOM au sujet des TIPE, sur le site de http://refmar.shom.fr/fr/documentati...88CC28A7CFEE9E . Quelqu'un sait-il si ces documents sont les mêmes que ceux de l'ancien lien ? Le problème étant que ce deuxième lien n'offre pas les informations que je recherche.

Premièrement, pour appliquer la formule harmonique du type h(t) = Z0 + Somme (Ai cos(qi t + Voi - Gi)), je cherche à déterminer les constantes harmoniques Ai et Gi pour un port donné. Je sais que ces données ne sont pas publiques mais que le SHOM met à disposition les moyens de les calculer. Cependant, après avoir pris contact, ils m'ont semblé assez fermé avec une réponse avoisinant : "Tu peux télécharger les mesures à tel endroit, et obtenir les constantes avec une analyse harmonique. Pour savoir comment faire cette analyse, tu peux livre ce livre". J'ai donc lu La marée océanique côtière, de Bernard Simon, mais je l'ai trouvé un peu trop théorique pour savoir que faire exactement pour appliquer les principes expliqués. Et j'avoue ne pas avoir compris les détails de tous les calculs non plus.
J'ai cru comprendre que je devais réaliser des filtres passe-bande, des transformées de Fourier, pour en déduire des vecteurs réduits Ck , et qu'il y aurait alors des systèmes d'équation à résoudre. Je ne comprends pas exactement quelles fréquences choisir, comment savoir à quel composante (K1, O1, P1, Q1, M2, S2, K2, N2) correspond tel pic du spectre après transformée de Fourier. Je n'ai pas compris non plus s'il était nécessaire de passer par la méthode des hauteurs réduites, ou des moindres carrés, où si l'on pouvait se contenter uniquement de TFR.
Où pourrais-je trouver des explications accessibles à un étudiant de deuxième année de prépa, pour déterminer les constantes harmoniques à partir d'une série de mesures de la hauteur d'eau sur une année ? L'absence de réponse du SHOM me fait penser qu'ils ont commencé à m'ignorer.

Deuxièmement, après l'obtention des constantes harmoniques Ai et Gi pour les 8 composantes auxquels je compte me restreindre dans un premier temps, je ne sais pas comment établir le reste de la formule harmonique (hauteur moyenne 20, pulsation de l'onde qi, argument V0i). J'avais déjà programmé des modélisations simples (la méthode des douzième, ou sinusoïdale) en me basant sur le chapitre I de http://educmath.ens-lyon.fr/Educmath...cret_tome2.pdf. Il suffisait d'initialiser la fonction à l'instant de basse mer du jour où l'on veut prédire la marée. Mais là, je ne vois pas comment fixer les arguments de toutes les composantes sinusoïdales, ni que prend pour le niveau moyen.

Des utilisateurs du site sauraient-ils répondre à ces questions, où sauraient-ils où trouver ces informations ?

[gts2]

La transformée de Fourier vous donnera tout : fréquence, phase, amplitude ...
Vous avez un module Python dans numpy fft pour faire le travail.
L'affectation des noms se fera à partir de la fréquence.
Un (gros) bémol : les données disponibles sont affectées de perturbation atmosphérique, ce qui fait qu'on ne peut raisonnablement trouver que les harmoniques les plus fortes.
Le niveau moyen est arbitraire, c'est un choix d'origine.

"après l'obtention des constantes harmoniques Ai et Gi" : avec quelle méthode, que ce soit théorique ou expérimentale, on obtient en même temps amplitude, phase, fréquence. Par Fourier, on obtient en fait la phase Voi - Gi. La distinction V0i Gi est une distinction entre V0i : la phase du potentiel générateur et Gi le retard de la réponse. Gi ne me parait pas évident à obtenir, alors que Voi résulte simplement du choix de l'origine des temps.

A moins que vous ne preniez le problème dans l'autre sens : vous vous donnez la fréquence (K1, O1, P1, Q1, M2, S2, K2, N2) et vous calculez la composante par transformée de Fourier (sans passer par la FFT) pour cette fréquence.

[gts2]

Quand j'ai dit sans passer par la FFT, je voulais dire sans récupérer la fonction A(f), mais il faudra utiliser une transformée de Fourier discrète (puisqu'on part de données échantillonnées limitées...) pour obtenir juste la valeur correspondant à la fréquence désirée.

[gts2]

Eventuellement un lien avec des exemples Python : [URL="http://www.tangentex.com/PythonTFD.htm#Par2"PythonTFD[/URL]

[Lomiop]

Bonjour,

j'essaye encore de procéder à une TFD sur les mesures, avec Python. Cependant le résultat n'est pas satisfaisant. J'essaye d'utiliser le module fft de numpy.

Voici mon code, j'aimerais savoir si j'ai mal utilisé la fonction.

## Lecture des mesures et création de la liste des mesures

mesures = open('Mesures Brest 2019.txt', 'r')
next(mesures)       #Ignorer la première ligne
liste_mesures = []
for ligne in mesures:
    decoupe = ligne.split(';')
    print(decoupe)
    liste_mesures.append(float(decoupe[1])) # Une ligne est du type ['01/04/2019 20:27:30', '2.4441', '1\n']

## Conversion de la liste en tableau, affichage de la courbe réel

tab_mesures = np.array(liste_mesures)
n = len(tab_mesures)
temps = np.arange(n)/60/24    # En jour
plt.figure('Courbe hauteur/temps')
plt.plot(temps, tab_mesures)
plt.show()

## TFD

Te = 60 # secondes
fe = 1.0/Te
T = n*Te

import numpy.fft
tfd = numpy.fft.fft(tab_mesures)
plt.figure('TFD')
plt.plot(temps, np.absolute(tfd)*2.0/n)
plt.show()

Voici la courbe réelle de la hauteur en fonction du temps, et la TFD obtenue, avec à chaque fois un zoom à droite.



J'ai mis l'unité en jour, pour vérifier que le résultat est cohérent. À noté que sur la courbe de hauteur, certains pics en 0 sont dus à des moments où aucune mesure n'avait été relevée. Ça peut durer un certain nombre de minutes. Je ne sais pas si je dois les gérer ça avant de faire la TFD.

Pour la TFD, en dehors d'un fondamental très élevé, je ne trouve que 2 pics à des fréquences peu cohérentes. Ça m'a tout l'air d'être faux.

[gts2]

Il me semblait que les données étaient en heures, donc temps=np.arange(n)/24 pour avoir le temps en jour.

Ceci étant votre graphe temporel a l'air cohérent, donc les données 2019 seraient toutes les minutes !

L'axe du spectre est la fréquence pas le temps.



Voici ce que j'obtiens (données en heures) : pic à
0,0788 heure-1 soit période de 12,68h N2
0,0804 soit 12,43 h M2
0,0832 soit 12 h S2

[gts2]

En abscisse du spectre, prendre :
freq = np.linspace(0, fe, n)

Remarque : en fait la seule partie utile est entre 0 et fe/2. C'est ce que vous avez déjà fait (deuxième graphe maxi 175 vs. 350 pour le premier), même si je ne le vois pas dans votre code.

[Lomiop]

En effet, les données étaient bien en heures.

Dans mon graphe, troisième image, le pic à 175h est-il le début de la partie fe/2 - fe ?

Avec quelles données avez-vous obtenu ce graphe ? En modifiant mon programme pour avoir les fréquences (freq ci dessus) en abscisse, le problème de l'allure des résultats est inchangé.



Je ne distingue pas plusieurs pics distincts, et je me demande pourquoi.

[gts2]

Vous avez pris les fréquences en Hz, ce qui rend le décodage peu lisible, vous avez un pic principal autour de 0,000022 Hz soit 0,079 heure-1=1/(12,6 heure) raisonnable ; ou 1,9 jour-1 soit une période d'en gros une demi-journée.
Donc le graphe est le bon.

Si vous faites un zoom autour de ce point, vous devriez trouver les pics attendus. Les quatre composantes autour de 12 heures sont à 12,417 ; 12 ; 11,97 ; 12,67 donc une variation max de l'ordre de 5%, donc les pics sont resserrés.

[petitmousse49]

Bonjour à tous
Je redécouvre ce sujet après une période d'absence. Pour répondre au message #13 de Lomiop : on trouve le détail de la méthode ainsi que les constantes harmoniques concernant le port de Brest ici :
http://refmar.shom.fr/documents/1022...ormulation.pdf
Pour les autres ports, il y a des correctifs à apporter. Si cela t'intéresse vraiment, je pourrai te retrouver les constantes du port des Sables d'Olonnes...

[OceanFlo]

Bonjour à tous,
Je suis également en cours de réalisation d'un modèle de calcul de marée à l'aide de python pour réaliser de la modélisation et vos explications sont vraiment très utiles !
petitmousse49, si tu as la possibilité, je suis preneur pour les valeurs de constantes du port de Boulogne sur Mer ou celles de Calais !
Merci à toi par avance !

[petitmousse49]

Le SHOM ne publie pas ses données pour diverses raisons. J'ai trouvé ceci sur le port de Boulogne : il s'agit de données un peu anciennes ; sans garantie de fiabilité !