Question sur le régime sinusoïdal

[Loosgin]

Oyé, oyé,

Je me suis appuyé sur ce cours : http://www.physagreg.fr/electrocinet...sinusoidal.php, qui est très bien expliqué, d'ailleurs. Grâce à ce dernier, je ne suis plus obligé d'apprendre bêtement les formules des dipôles éléectriques lorsqu'ils sont en régime sinusoïdal. Cependant, 3 incompréhensions persistent.

Etude du dipôle RC

Un générateur impose aux bornes de RC, une tension e(t)=E cos(ωt+ϕ). -> OK


Ils appliquent la loi des mailles dans ce circuit simple où les dipôles sont tous placés en série : u(t)+Ri(t)=e(t). ->OK

Ils utilisent la notation complexe ⟺ u(t)+Ri–(t)=E * expo( j(ωt) ). -> OK car à toute forme sinusoïdale, on peut lui associer une grandeur complexe (je sais, je sais, je prêche des converties)

i(t)=Cdu(t) / dt et i(t)=Cdu(t)/dt=jCωu(t) <=> i(t) = jCωu(t). -> Eh oui ! Deriver un signal sinusoïdal revient à le multiplier (en nombre complexe) par jω.

Premier point bloquant

u(t)+jRCωu(t)=Eej(ωt) KO -> Pourquoi l'intensité traversant la résistance peut être substituée par la relation intensité/tension du condensateur ?!
L'une des raisons à cela, (dites-moi si c'est n'importe quoi) le condensateur agit sur l'intensité du courant un peu comme un barrage situé dans un fleuve agit sur le courant d'eau. Autrement expliqué : on peut dire que le condensateur donne en quelque sorte le tempo du courant ?

Deuxième point bloquant

u(t)=U * exp(jϕ) * exp(jωt) <=> U = u(t), cette équivalence est-elle correcte ?

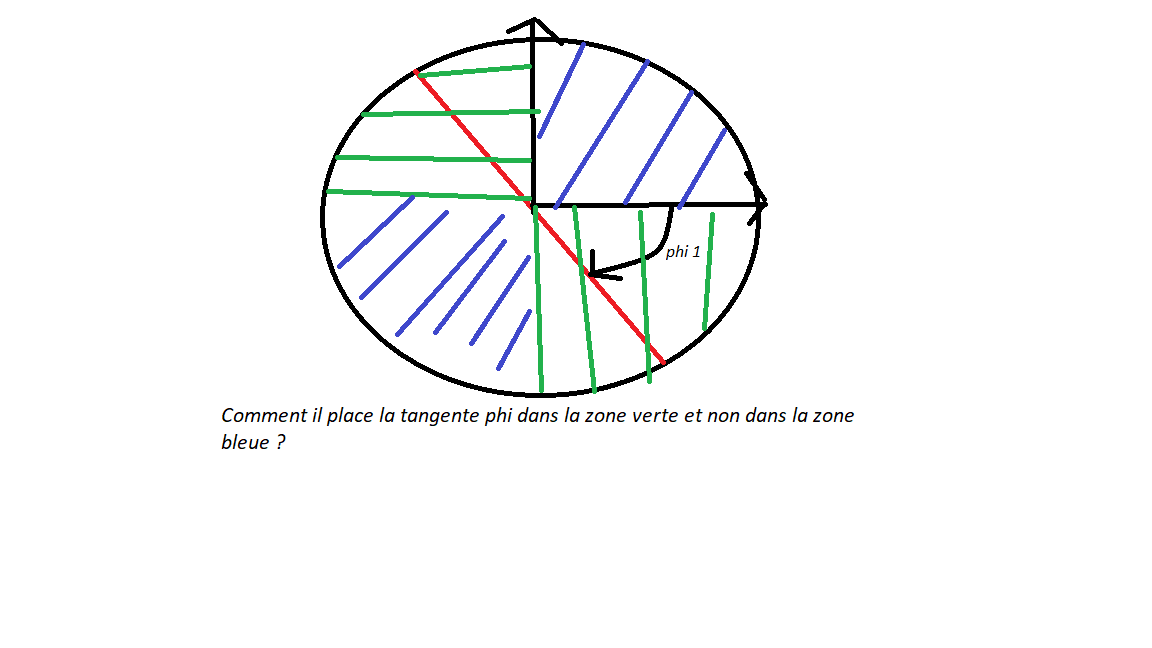
Troisièmepoint bloquant

tan( phi ) = −RC ω
Il place cet angle soit dans le premier quart du cercle en partant de 0 et dans le sens trigonomètrique soit dans le dernier quart. J'ai compris que la fonction tangente a une précision au pi près. Cependant, je n'arrive pas à comprendre comment il sait que la tangente se situe dans ces 2 quarts et non dans les 2 autres

Pour illustrer mes derniers propos (je l'accorde, ils sont peu limpides) :



Je vous remercie par avance pour toutes réponses.
-----

[calculair]

bonjour

La charge d'un condensateur est Q = C V donc dQ/dt = C dV/dt car C est constant

dQ/dt est le courant i ( Q = i t et dQ/dt = i )

Si V(t) = E exp (J w t) alors dV/dt = J w E exp (J wt ) = Jw V(t)

[Loosgin]

Merci pour votre réponse. Mais pourquoi cela au i (t) de i (t) * R.

i (t) * R est la tension aux bornés de la resistance. Pourquoi emploie-t-on la relation intensité/ tension du condensateur aux bornes de la résistance?

[stefjm]

Dans un circuit série, le même courant circule dans les deux éléments.
On peut donc substituer le courant par sa valeur en fonction de la tension du condensateur.

[A voir en vidéo sur Futura]

[Loosgin]

Si je comprends bien, le choix est arbitraire. Si c'était un circuit RLC en série, j'aurais très bien pu remplacer l'intensité des dipôles par la relation intensité/tension du condensateur ou par la relation intensité/tension de la bobine ?

[Chtulhu]

Bonjour,

comme il a été dit précédemment, i est commun aux 3 éléments en série.

vL=Ldi/dt, avec i=dq/dt => vL=Ld(dq/dt)/dt=Ld²q/dt²

Bien voir que iL est nul à t(0+) et uC est nul à t(0+), si on considère tout le monde déchargé à t=0

[Loosgin]

Merci, j'aurai une meilleur lorsque je ferai des exercices.


et vous savez me dire pour les 2 autres incompréhensions ?