Bonjour à tous!
Soit dans C l'équation fonctionnelle suivante (voir pj) où f_chapeau est un opérateur complexe , psi_m est une fonction complexe et f_m une constante complexe. Je dois prendre le complexe conjugué de cette équation, et j'ai un doute dans l'ordre des termes ??? Merci d'avance pour votre aide!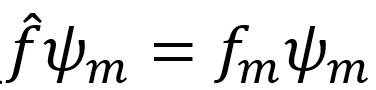
Bonjour,
C'est une équation aux valeurs propres, pas un produit hermitique (produit scalaire dans un espace de Hilbert). Pourquoi doutez-vous de l'ordre des termes ?
Not only is it not right, it's not even wrong!
Merci pour ta réponse!
Je travaille actuellement sur le tome II du cours de physique de Landau et Lifchitz "Mécanique Quantique", et, page 20, je n'arrive pas à retrouver le résultat de la dernière équation... Voici l'extrait:
La formulation de la dernière phrase est un peu trop raccourcie, ce qu'il faut faire :
1) multiplier la première équation par
2) multiplier la seconde équation par
3) soustraire la seconde de la première.
La première multiplication donne :
Merci pour ta réponse!
Jusque là, ça va ... c'est ensuite que j'ai des doutes ....
Re,
À mon avis, c'est une forme de masochisme...Envoyé par Jon83
Landau & Lifschitz sont parfois un peu rapides sur les explications et justifications mathématiques. Le terme 'égalité complexe conjuguée" est un raccourcis (de mon point de vue).
En repartant de la définition de l'adjoint d'un opérateur et avec quelques manipulations vous devriez arriver à prouver la relation qui vous pose problème. En n'oubliant pas que l'opérateur ici est hermitien (auto-adjoint).
Ajout : je viens d'ouvrir mon tome 2 du cours de L&L, il faut aussi tenir compte du fait que l'opérateur f correspond à une observable réelle.
En fait, tout est donné dans ce qui précède votre extrait (mais la mise en page de mon livre n'est pas du tout celle de l'extrait que vous avez posté. C'est quelle édition ?).
Dernière modification par albanxiii ; 15/05/2018 à 06h50.
Not only is it not right, it's not even wrong!
Bonjour!
Merci pour ta réponse ...
1) je ne maîtrise pas encore suffisamment bien la manipulation des opérateurs adjoints, hermitiens ...
2) c'est l'édition MIR 1966 (probablement la 1ère? mais ce n'est pas indiqué). L'extrait que j'ai envoyé est une remise en forme manuelle sous Word, que j'effectue au fur et à mesure de mon avancement ...
il y a une notation interessante mais que je suis incpable d'écrire ici en latex
elle untilise une double fleche <-> au dessus d'un opérateur
c'est du genre <f1 O^{<-> f2>
elle signifie qu'il opere d'abord a droite puis a gauche et qu'on fait la soustraction
si quelqu'un sait l'écrire proprement ce serait bien de nous en faire profiter.
O^\leftrightarrow
ou alors
\overleftrightarrow{O}
Dernière modification par Sethy ; 15/05/2018 à 10h49.
La double flèche est normalement utilisée pour les dyadiques. Je ne l'ai jamais vu dans le contexte d'opérateurs agissant à gauche ou à droite...
il y'a une note en bas de la page d'avant (19), le reste est bien expliqué, mais aller directement aux tomes de L&L sans bagage mathématique complet, il faut diversifier les références pour se rendre compte de leur style ...
je n'ai pas retrouvé dans quel bouquin il y avait cette notation mais elle avait rapport avec le vecteur densité de courant d'un champ chargé.
on a
qui était noté
