Bonjour,
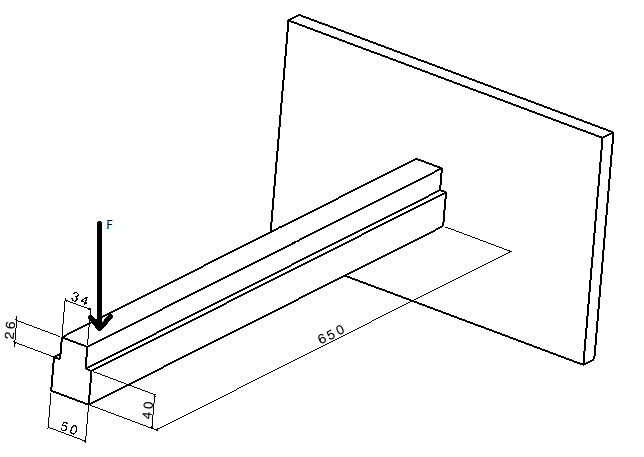
J’aurais besoin de connaitre la flèche maximum à l’extrémité d'une poutre en acier et fixé à son autre extrémité .
Celle ci n'est pas de section carré ou rectangulaire et la force exercé en son bout est de 294 N.
Merci pour votre aide
-----

Bonjour,
J’aurais besoin de connaitre la flèche maximum à l’extrémité d'une poutre en acier et fixé à son autre extrémité .
Celle ci n'est pas de section carré ou rectangulaire et la force exercé en son bout est de 294 N.
Merci pour votre aide


Bonjour Plume29,
C'est le calcul d'un cantilever, dans votre cas j'obtiens une flèche de 0.14159 [mm] pour une charge de 294 [N] à son extrémité, par simulation.
Cordialement.
Jaunin__


Bonsoir,
Juste une précision : il faut évidemment que la tôle verticale soit suffisamment épaisse pour pouvoir négliger sa déformation (qui, sinon, augmenterait alors beaucoup le déplacement en bout de poutre).
Cordialement

Oui, j'ai mis de l'épaisseur.

Merci pour vos réponses.
Pouvez vous me dire, le calcul qu'il faudrait que je pose pour obtenir le résultat, car il faut que je puisse le démontrer et comprendre la méthode.
En faite la poutre est fixé à un mur qui ne risque pas de bouger.

La formule avec la charge à l'extrémité pour la flèche est :
f= (P*L^3)/(3*E*J)
P=294 [N]
L=650 [mm]
E=210 [GPa]
B=50 [mm]
H=66 [mm]
J=(B*H^3)/12 [mm^4] en gros.
Ce n'est pas la valeur juste de votre forme.
Il faut trouver la valeur de J.
La formule ne donnera pas le même résultat que la simulation.
Avec l'approximation j'ai une flèche de 0.107 [mm] au lieu de 0.14159 [mm]

bonjour,
Module de young 21000daN/mm²
Inertie de votre profilé 98,4063cm4
centre de graviité en x=3,0115cm
Moment de flexion sous la charge de 29,4daN soit 29,4x0.650=19,11daN.m
calcul de la flèche a l'extrémité par Verechaguine
= ['19,11x0.65x0.5)2/3x0.65]/21E9x98.4063E-8=0.00013023m soit 0.130mm
en négligeant la flèche due a l'effort tranchant terme négligeable
si on tient compte du poids propre de votre profilé soit 23.69kg/m
la flèche due au pods propre['5x0.650x0.33333)0.750x0.650]/21e9x98.4063E-8=0.000025579m soit0,02557mm
la flèche totale a l'extrémité est de 0.13mm+0.0255mm=0.155mm
la flèche a l'extrémité en négligeant le poids propre est de 0.13mm,sans le poids propre
cordialement
géagéa
ais

Bonjour,
merci pour vos réponses.
Jaunin je comprends votre calcul et c'est celui auquel j'ai pensé mais il n'est pas précis car il est adapté pour une poutre carré ou rectangulaire.
Geagea, je comprends pas du tout votre calcul.

Bonjour Plume29,
Vous avez tout à fais raison, pour simplifié j'ai pris une poutre rectangulaire.
Geagea que je salue vous a donné le moment quadratique juste passant par le centre de gravité de votre pièce :98,4063cm4.
Mais il faut le calculer.
Dans la formule avec ce J, j'obtient 0.13 [mm]
En simulation avec le poids propre j'ai une flèche de 0.16224 [mm].
Cordialement.
Jaunin__

bonjour,
en tenant compte du poids propre,je présume que vous avez calculer le poids propre avec une section rectangulaire
,si en veut aller plus loin il faudrait tenir compte de la flèche due a l'effort tranchant,mais ce terme est négligeable pour les sections massives,hormis pour les potres en treillis
cordialement
géagéa

bonjour Plume 29
que voulez vous savoir,car apparemment vous n'avez pas compris mon calcul
cordialement
géagéa

Bonjour Geagea,
Non le calcul est fait avec la vrai forme de la poutrelle.
Cordialement.
Jaunin__
Gros soucis avec FS Forum

bonjour,
les valeurs sont pratiquement identiques,
cordialement
géagéa

Une petite méthode pour le calcul du moment quadratique de la forme T

bonjour
il y a une erreur,essayez de décomposer vos surfaces,et centre de gravité de chaque élément,calcul du moment statique,et du centre de gravité,attention aux formules toutes faites
cordialement
géagéa

Bonjour Geagea,
Je trouve bien la même chose que vous, non ?
@Geagea #7
Inertie de votre profilé 98,4063cm4
La total :
AIRE = 2.8840000e+03 MM^2
CENTRE DE GRAVITE relatif au repère _ :
X Y 0.0000000e+00 -9.8848821e+00 MM
INERTIE relative au repère _ : (MM^4)
TENSEUR D'INERTIE*:
Ixx Ixy 1.2658613e+06 0.0000000e+00
Iyx Iyy 0.0000000e+00 5.0182533e+05
MOMENT POLAIRE D'INERTIE*: 1.7676867e+06 MM^4
INERTIE au CENTRE DE GRAVITE relative au repère _ : (MM^4)
TENSEUR D'INERTIE*:
Ixx Ixy 9.8406311e+05 0.0000000e+00
Iyx Iyy 0.0000000e+00 5.0182533e+05
Moments surfaciques d'inertie par rapport aux axes principaux: (MM^4)
I1 I2 5.0182533e+05 9.8406311e+05
MOMENT POLAIRE D'INERTIE*: 1.4858884e+06 MM^4
MATRICE ROTATION _ orientée par rapport aux AXES PRINCIPAUX :
0.00000 -1.00000
1.00000 0.00000
ANGLE DE ROTATION _ orienté par rapport aux AXES PRINCIPAUX (degrés):
Autour de l'axe z 90.000
RAYON DE GYRATION PAR RAPPORT AUX AXES PRINCIPAUX*:
R1 R2 1.3191029e+01 1.8471997e+01 MM
Module section et points correspondants*:
MODULE 1 2 COORD
Autour de l'A 2.00730e+04 MM^3 9.8849e+00 -2.5000e+01 MM
2.00730e+04 MM^3 9.8849e+00 2.5000e+01 MM
Autour de l'A 3.26767e+04 MM^3 -3.0115e+01 2.5000e+01 MM
2.74228e+04 MM^3 3.5885e+01 1.7000e+01 MM

bonjour jaunin
en effet on trouve les mêmes valeurs,excusez moi j'ai répondu hativement ,tout rentre dans l'ordre
cordialement
gégaéa

Coucou
Je trouve bien comme Jaunin, une inertie de 98.4 cm4 pour cette section, ce qui conduit à une flèche hors poids propre et hors effort tranchant de 0.146 mm.
Attention :ça n'existe pas. Il y a toujours une élasticité du mur, et de la plaque, donc de l'assemblage. Donc, il y a une rotation d'appui qui va ajouter de la flèche au bout de la console.En faite la poutre est fixé à un mur qui ne risque pas de bouger.
C'est ce qui fait d'ailleurs tout le charme du calcul des assemblages en charpente acier. Je ne pense pas que Géagéa me contredise sur ce point ?

Ooups, je voulais dire je trouve 0.13 mm comme géagéa

bonjour Ilovir,
en effet,je suis d'accord,un encastrement parfait n'existe pas en pratique,lors des assemblages métalliques,assemblages des jarrets de portique,on a un assemblage élastique
cordialement
géagéa

