Le centre de gravité du cercle

[Echo83]

Bonjour, j'ai une question par rapport au moment statique d'un cercle. Avec théorème de GULDIN si c'est possible, mais je n'arrive pas comprendre comment faire. Merci d'avance !
Voila se que j'ai trouvé.

-----

[jacknicklaus]

dans ton cours, tu as dû apprendre que le moment statique d'une section (homogène) par rapport à un axe est le produit de l'aire de la section par la distance entre l'axe et le centre de masse de cette section.
- quelle est l'aire à considérer ?
- où est le centre de masse d'un cercle ?
- quelle est sa distance à l'axe ?

conclure.

[phys4]

Bonjour, j'ai une question par rapport au moment statique d'un cercle.

Bonjour,
Et merci de respecter les termes mathématiques : un cercle est le bord d'un disque, et n'a pas d'aire, seulement une longueur.

[Echo83]

Bonjour,
L'énoncé du problème:
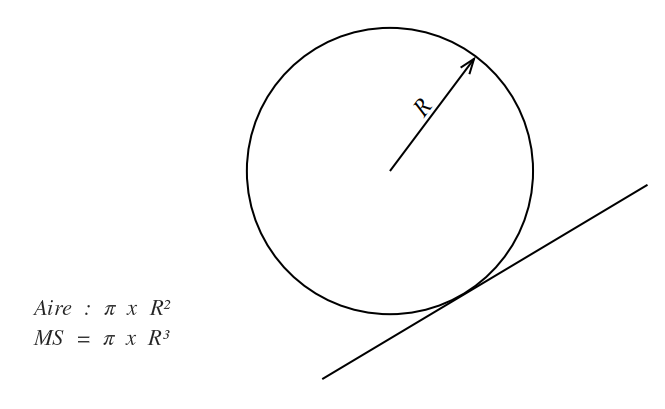
Calculer le moment statique d'un cercle par rapport à un axe tangent à celui-ci. Le rayon de cercle est R.


- où est le centre de masse d'un cercle ? Au centre
- quelle est sa distance à l'axe ? 2 pi OG

Pour l'autre question ne n'ai pas trop compris.
- quelle est l'aire à considérer ? ....

Mes cours sont assez dur a comprendre...mais j'ai un cours sur le théorème de Guldin qui nous dit : 2 pi OG A.

[A voir en vidéo sur Futura]

[coussin]

Qu'est-ce-que OG?

[jacknicklaus]

Bonjour,
L'énoncé du problème:
- où est le centre de masse d'un cercle ? Au centre

oui

- quelle est sa distance à l'axe ? 2 pi OG

mais non ! ton axe est tangent au cercle, il est donc distant de R de son centre !

Enfin, quelle est l'aire délimitée par un cercle de rayon R. L'aire d'un disque de rayon R si tu préfères. Ca n'est pas compliqué ! non ?

le théorème de Guldin qui nous dit : 2 pi OG A

Tu ecris des choses qui n'ont pas de sens. En l'occurence Guldin donne un moyen habile de calculer le volume d'une surface de révolution : c'est le produit de la surface (= une "section" du volume final) multiplié par le périmètre d'un cercle de rayon égal à la distance entre l'axe de révolution et le centre de masse de la section.

Appliqué à un disque de rayon R, dont la distance entre le centre et l'axe de révolution serait noté a, Guildin dit que V = (pi.R²).(2.pi.a) = 2.pi².R².a

il y a un lien évident entre volume d'une surface de révolution et moment statique de la surface : V = 2.pi.Ms (se ramener à la définition par les intégrales). C'est un autre moyen de calculer Ms à partir de V, et d'utiliser Guldin pour calculer V.

la formulation "le moment statique d'une section (homogène) par rapport à un axe est le produit de l'aire de la section par la distance entre l'axe et le centre de masse de cette section" est en fait équivalente au théorème de Guldin.

[Echo83]

OG c'est la distance entre le centre de rotation et le centre de gravité de la surface.

L'aire est d'un disque est pi.R²

[jacknicklaus]

oui, et donc tu as compris maintenant pourquoi Ms = pi.R³ ?

[Echo83]

Non tout...dsl

[jacknicklaus]

Procédons alors par étape.
est-ce que tu es d'accord avec "le moment statique d'une section (homogène) par rapport à un axe est le produit de l'aire de la section par la distance entre l'axe et le centre de masse de cette section."

Si oui, il n'y a rien de plus à comprendre que Ms = Aire.distance = (pi.R²).R = pi.R³
Sinon, à toi de donner (très précisément) ce que ton cours utilise comme définition et/ou méthode de calcul du moment statique


PS

Non tout...dsl

il manque des touches à ton clavier ???

[Echo83]

Ha d'accord !! j'ai compris !

[Echo83]

Pouvez - vous me corriger ce exercice s’il vous plaît..?
Problème 3 D.png

daum_equation_1530263883598.png