Bonjour,
Je suis nouveau sur le forum et ma première question porte sur la statistique d'échange des particules.
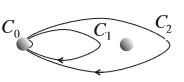
Dans le cas 3D, on justifie les statistiques fermionique et bosonique en disant qu'une particule qui retourne à sa position initiale après avoir parcouru un chemin quelconque doit avoir un état quantique identique à l'état de départ car tous les chemins sont équivalents. En effet, même s'il existe d'autres particules, on peut toujours déformer le chemin C2 en C1 en contournant les particules. In fine la phase qu'acquiert le système après l'échange de deux particules doit être +1 ou -1 pour que deux échanges consécutives de particules qui est équivalent à une particule contournant une autre particule redonne le même état quantique ( -12 = 1 et 11 = 1).
Dans le cas 2D, par contre, les chemins C1 et C2 de la figure ne sont pas équivalents car on ne peut pas déformer C2 en C1 tout en évitant la particule de droite. Donc les états quantiques initiale et finale ne sont pas les mêmes.
Mes questions sont :
Pourquoi la statistique d'échange dépend des caractéristiques topologiques ? Quel est le point physique qui se cache derrière tout çà ? Pour moi, que la particule emprunte le chemin C1 ou C2, l'état final reste identique à celui de départ. Pourquoi le fait qu'il y est une particule en 2D influence l'état final alors qu'on ne suppose aucune interaction ?
Si quelqu'un pouvait m'éclairer car j'ai l'impression que tout le monde explique çà comme si c'était évident que la statistique d'échange dépende des caractéristiques topologiques. J'ai lu nul part une justification claire, donc soit on justifie proprement ou soit on dit clairement que c'est un postulat !!!
Merci
-----