La vie et l'entropie

[yvon l]

Je pense que de ne voir l'entropie que comme une mesure de la "qualité" de l'énergie fait passer à côté de pas mal de choses.

Un exemple. Imaginons deux solutions aqueuses distinctes à même concentration, de deux substances proches (par exemple deux "sucres" ayant la même formule chimie mais reflets l'un de l'autre dans un miroir, comme le D- et le L-Glycéraldéhyde https://fr.wikipedia.org/wiki/Glycéraldéhyde ).

Leur énergie est parfaitement identique. Si je les mets en contact (en enlevant la plaque qui les sépare par exemple), il ne va pas y avoir de variation d'énergie. Et pourtant, l'entropie va fortement augmenter puisque les deux substances vont se mélanger.

Alors que si de part et d'autre de la paroi, j'avais les mêmes substances, il n'y aurait ni variation d'énergie, ni variation d'entropie (l'entropie totale étant rigoureusement égale à la somme des entropies des deux solutions).

Merci, très bonne remarque qui demande réflexion. Pour celle-ci, peux-tu me dire si le mélange se fait spontanément (pas d'apport d'énergie via par exemple l'agitation des liquides).
-----

[Sethy]

Merci, très bonne remarque qui demande réflexion. Pour celle-ci, peux-tu me dire si le mélange se fait spontanément (pas d'apport d'énergie via par exemple l'agitation des liquides).

Pense à la goutte d'encre qui tombe dans l'eau. Aucune agitation, autre que celle liée à la température interne du liquide n'est nécessaire à sa diffusion.

Et rappelons que même au zéro absolu, l'énergie de vibration d'un oscillateur harmonique quantique n'est pas nulle puisqu'elle vaut (N+1/2) hv, donc même avec N=0, il reste le terme 1/2 hv).

[Sethy]

Il faut également considérer l'opération inverse : comment séparer la goutte d'encre de l'eau une fois la solution homogène.

[yvon l]

Il faut voir si l'augmentation d'entropie de la diffusion n'est pas accompagnée d'une variation de température ??

[invite6486d7bd]

Il faut également considérer l'opération inverse : comment séparer la goutte d'encre de l'eau une fois la solution homogène.

Une gravité élevée fera l'affaire...

[Sethy]

Une gravité élevée fera l'affaire...

Vous venez de résoudre le problème de l'eau potable dans le monde ...

[Sethy]

Il faut voir si l'augmentation d'entropie de la diffusion n'est pas accompagnée d'une variation de température ??

Mélanger, même un sirop de sucre très concentré avec de l'eau ne provoque pas de variation de température décelable (peut être avec un thermomètre au 1/10ème) mais en tout cas, rien en comparaison du gain d'entropie observé.

[Sethy]

D'ailleurs, ce gain, on peut le sentir en faisant une expérience toute simple.

Imaginons un récipient contenant "4 atomes", 2 de colorants (X) et 2 d'eau (O).

Le nombre de combinaisons possible est de 4!/(2! 2!) = 6

XX XO XO OX OX OO
OO XO OX XO OX XX

Si on considère que la situation "séparée" est celle où tous les molécules de colorants sont à gauche ou à droite, il y a donc 2 cas / 6, soit 1 chance sur 3.

Imaginons maintenant, qu'on ajoute à nouveau 2 atomes de colorants et 2 atomes d'eau, le nombre de possibilité est de 8!/(4! 4!) = 70

Ici également, le cas "séparé" est celui ou les 4 molécules de colorants sont soit à droite, soit à gauche, il y a donc toujours 2 chances, mais sur 70.

Si on double à nouveau pour obtenir 8 molécules de colorants et 8 d'eau, il y a 12870 possibilités avec toujours 2 "chances" de se trouver avec les 8 molécules de colorants d'un côté ou de l'autre.

Avec "à peine" 32 molécules de chaque, il y a 1,8.10^18 possibilités.

Pour info, depuis la création de l'univers, il ne s'est écoulé que 4,3.10^17 secondes ...

Donc rien qu'avec 64 molécules en tout, il faudrait faire un tirage toutes les secondes depuis le début de l'univers pour être dans l'ordre de grandeur des solutions possibles.

Alors imaginez avec même 1 micro-litre d'air (une point de "bic") qui contiennent non pas 64 atomes mais 2,7.10^16 ... la probabilité de retrouver tous les azotes d'un côté et tous les oxygènes de l'autre.

L'entropie, c'est (aussi) ça.

[Sethy]

Deux effets viennent "tempérer" ce résultat.

Le premier, c'est "l'indiscernabilité totale", qui est un phénomène quantique qui empêche de distinguer les molécules de même nature entre elles, sinon, il n'y aurait pas X et O mais X1, X2 et O1, O2, ce qui démultiplierait encore les possibilités (loi en N!). Avec 64 atomes, il n'y aurait pas 10^18 possibilités mais 10^89 ...

La seconde, c'est que le calcul que j'ai fait s'approche de celui du nombre de complexion (oméga) et que la vrai formule fait intervenir le logarithme de ce nombre via la célèbre formule de Boltzman :



Et d'ailleurs si on prend les logarithmes des chiffres obtenu précédemment, on remarque qu'ils doublent (approximativement bien sûr) à chaque fois :

oméga   ln(oméga)
6	1,791759469
70	4,248495242
12870	9,462654301
601080390	20,21423924
1,83262E+18	42,05228057

[Sethy]

Trop tard pour éditer, mais pour les logs, j'ai été un peu vite car si on calcule le Delta S, en prenant 6 combinaisons x 6 combinaison (cas où mélange 2x4 atomes), on passe de 36 configurations initiales à 70 finales. Donc ici, il faut remarquer qu'on fait plus que doubler.

L'exercice avec les logs est plus pertinent si on prend de simples dilutions et qu'on rajoute simplement de l'eau à chaque fois, mais ce n'est pas très important.

[yvon l]

Mélanger, même un sirop de sucre très concentré avec de l'eau ne provoque pas de variation de température décelable (peut être avec un thermomètre au 1/10ème) mais en tout cas, rien en comparaison du gain d'entropie observé.

Bonjour et merci pour vos commentaires.
Si l’arrangement moléculaire (force de liaison) diffère avant et après le mélange, la variation d’énergie correspondante peut être empruntée à l’énergie thermique .

Dans le cas de deux liquides de densité différente, le centre de gravité remonte après mélange. Il faut donc fournir de l’énergie pour compenser l’augmentation du potentiel gravitationnel du mélange. Donc une variation d’énergie petite peut engendrer une grande variation d’entropie.

[Amanuensis]

Discuter l'entropie pour elle-même est une «ornière» usuelle dans ce forum!

On s'est éloigné du sujet, le message #1 a mis en gras «La question porte sur la naissance de l'organisation dans les cellules vivante.»

[Sethy]

Bonjour et merci pour vos commentaires.
Si l’arrangement moléculaire (force de liaison) diffère avant et après le mélange, la variation d’énergie correspondante peut être empruntée à l’énergie thermique .

Dans le cas de deux liquides de densité différente, le centre de gravité remonte après mélange. Il faut donc fournir de l’énergie pour compenser l’augmentation du potentiel gravitationnel du mélange. Donc une variation d’énergie petite peut engendrer une grande variation d’entropie.

J'avais exprès pris l'exemple des deux solutions fabriquées exactement à partir du même composé, qui présente juste la particularité d'être reflet l'un l'autre dans le miroir. Ces solutions ont donc même concentration, même densité, même énergie, ... Et malgré tout elle se mélange spontanément et leurs entropie croit énormément sans que leur énergie ne varie significativement.

En plus, la raison de la spontanéité de ce mélange, je l'ai expliqué avec l'histoire des colorants.

Il faut accepter que l'entropie est une grandeur qui se manifeste à la fois "macroscopiquement" et peut servir d'une certaine manière d'indicateur sur la perte de "qualité" de l'énergie au cours d'une transformation, mais qu'elle prend sa source dans des phénomènes microscopiques dont certains effets ne s'expliquent pas par la seule approche macroscopique.

[Sethy]

Discuter l'entropie pour elle-même est une «ornière» usuelle dans ce forum!

On s'est éloigné du sujet, le message #1 a mis en gras «La question porte sur la naissance de l'organisation dans les cellules vivante.»

Non, je ne suis pas d'accord.

Je pense au contraire que les précisions sur l'entropie statistique sont essentielles car justement la méconnaissance de ce sujet induit un biais dans certaines interventions.

En plus, en raison de la taille des organites cellulaires, je pense notamment à celles des mitochondries (j'ai fait un rapide calcul, si elle n'était composée que de molécules d'eau les petites mitochondries en refermeraient 150.000 seulement) fait que l'aspect microscopique ne peut être éludé.

Si je prends cet organise comme exemple, c'est parce qu'on pense qu'il est le résultat de l'évolution d'un symbiote mais qui a fini par perdre son autonomie. Autrement dit, il fut un temps où c'était probablement un être vivant à lui tout seul.

[Sethy]

A titre de comparaison, une petite bactérie comme Escherischia Coli, a un poids équivalent à 10^10 molécules d'eau.

[yvon l]

Il faut accepter que l'entropie est une grandeur qui se manifeste à la fois "macroscopiquement" et peut servir d'une certaine manière d'indicateur sur la perte de "qualité" de l'énergie au cours d'une transformation, mais qu'elle prend sa source dans des phénomènes microscopiques dont certains effets ne s'expliquent pas par la seule approche macroscopique.

Oui, je suis d’accord avec toi. Par contre ta remarque me ferait dire qu’il faudrait peut-être creuser sur l’aspect informationnel lié à l’entropie. La diminution d’entropie correspond à une apparition au niveau macroscopique d’informations pertinentes au niveau macroscopique auquel on s’intéresse. Par exemple au niveau de la cellule en ce qui concerne la vie.
L’apparition d’information la plus simple est déjà en soi la création des flux d’énergie.
Par exemple, la chaleur (flux d’énergie thermique) due au déséquilibre entre 2 sources d’énergie à des températures différentes est la manifestation de l’apparition d’un transfert organisé d’une énergie complètement désorganisé au niveau microscopique. L’information associée correspond au transfert d’énergie (Q). C’est en quelque sorte une propriété émergente.

[Sethy]

Dommage, on avait réussi jusqu'ici à ne pas polluer le débat avec l'entropie informationnelle qui je le rappelle :

"At an everyday practical level the links between information entropy and thermodynamic entropy are not evident. Physicists and chemists are apt to be more interested in changes in entropy as a system spontaneously evolves away from its initial conditions, in accordance with the second law of thermodynamics, rather than an unchanging probability distribution. And, as the minuteness of Boltzmann's constant kB indicates, the changes in S / kB for even tiny amounts of substances in chemical and physical processes represent amounts of entropy that are extremely large compared to anything in data compression or signal processing.".

Donc ici, justement comme on parle du second principe, basé sur des phénomènes spontanés, le recours à cette approche me semble donc peu pertinente au regard de ce qui est écrit.

A la limite même, la dernière phrase "S / kB for even tiny amounts of substances in chemical and physical processes represent amounts of entropy that are extremely large compared to anything in data compression or signal processing" nous rapproche du sujet.

De très petites quantités de substances mélangées "produisent" une très large quantité d'entropie, j'ajoute ici "sans variation d'énergie pondérable".

[Sethy]

Pour revenir à la question initiale, je vais répondre de manière qualitative.

Je me souviens d'avoir lu (ou vu) un exposé de Prigogine à propos des cellules de Bénard (j'ai déjà cherché ce document depuis, sans succès). Et ce qu'il disait était intéressant, c'est que souvent on commettait l'erreur de ne voir dans ce dispositif (qui je le rappelle est constitué d'une plaque chaude sur laquelle se trouve un fluide lui même surmonté d'une zone froide) qu'un moyen de transférer plus efficacement les calories de la zone chaude vers la zone froide.

Si c'est effectivement vrai, la où résidait l'erreur d'interprétation selon Prigogine est de ne limiter la création d'entropie qu'à cet aspect, alors que selon lui, partout où il y a gradient, il y a création d'entropie. Et donc si on observe ce schéma en coupe qui provient du site http://www.astrosurf.com/luxorion/ch...dynamique2.htm on voit très bien cette source "secondaire" de création d'entropie.



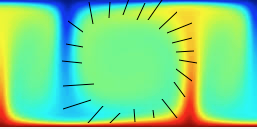
Image sur laquelle j'ai indiqué l'importance des gradients.

Si j'évoque cela, c'est parce que je pense (avis personnel, mais que je ne considère pas comme une théorie) que si les déséquilibres initiaux sont très importants, tels que ceux présents dans les fumerolles océaniques, un seul système (ou plutôt plusieurs membres d'une même familles) ne peut pas à lui seul créer l'entropie maximale que ce déséquilibre permet. Il y a donc (selon moi) de la place pour plusieurs systèmes cohabitants et utilisant chacun une "tranche" du déséquilibre initial au mieux. Un peu comme une marchandise qu'on ne va pas acheter à l'usine mais qui passe par un réseau de grossiste, semi-gros, détaillant. Une sorte de pyramide alimentaire.

Si on suit cette logique, ça explique pourquoi il peut exister plusieurs espèces d'individus. Mais aussi, ça répond à la question initiale à savoir que certaines espèces ont pu cohabiter d'abord, coopérer ensuite pour donner lieu à des symbioses. Ou qu'une même cellule a pu donner plusieurs cellules filles qui en s'accolant et se spécialisant ont pu mieux utiliser le déséquilibre que ne le faisait l'espèce de la cellule mère seule.

Ca ne constitue pas un "argument" et c'est qualitatif, mais je pense que ça donne un éclairage sur si pas le chemin suivi, au moins l'apparente contradiction soulevée dans la question initiale.

[yvon l]

Dommage, on avait réussi jusqu'ici à ne pas polluer le débat avec l'entropie informationnelle (..)

Pour ma part, si on veut avancer il faut en passer par là.

Pour illustrer voici un lien vers la thèse de Rodrick Dewar*:
Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states

Voir résumé
Une recherche sur le mot-clé information donne 27 occurrences
https://arxiv.org/pdf/cond-mat/0005382.pdf

[Sethy]

Quatre réflexions :
1) C'est une théorie que je ne connais pas, donc je ne peux pas en dire grand chose,
2) De ce que j'en lis (extrait cité), elle s'applique à une toute autre échelle que celle des phénomènes chimiques et physiques courants. Donc, je ne dis pas qu'elle est fausse (loin de là) mais qu'il s'agit au mieux d'extrapolation, avec tous les risques inhérents à extrapoler très loin du domaine de validité d'une théorie.
3) Je suis prêt à reconsidérer mon point de vue si on me montre en quoi ça ajoute à la compréhension (= simplification car le message #46 par exemple complexifie les choses pour moi plutôt que de les simplifier et me fait fortement penser à "pluralitas non est ponenda sine necessitate") ou si par exemple, on prend l'exemple de la diffusion du colorant et qu'on me montre (dans les chiffres) l'éclairage que cette théorie apporte.
4) je précise que je ne suis pas fermé, John Nash a par exemple montré des similitudes entre les problèmes qu'il étudiait et la notion d'entropie. Et effectivement, il y a un parallèle mais l'approche de Nash ne peut pas être utilisée pour calculer l'entropie d'une simple détente d'un gaz.

[yvon l]

Quatre réflexions :
1) C'est une théorie que je ne connais pas, donc je ne peux pas en dire grand chose,
2) De ce que j'en lis (extrait cité), elle s'applique à une toute autre échelle que celle des phénomènes chimiques et physiques courants. Donc, je ne dis pas qu'elle est fausse (loin de là) mais qu'il s'agit au mieux d'extrapolation, avec tous les risques inhérents à extrapoler très loin du domaine de validité d'une théorie.(..)
.

Bon, j’aurais du commencer par la biographie de Dewar*:
http://biology.anu.edu.au/people/roderick-dewarJe
En voici un extrait .
His current research looks at the emergent behaviour of complex biological and physical systems - whether individual organisms, ecosystems, turbulent fluids or Earth's climate system - from the common viewpoint of entropy, as the statistical outcome of a large number of underlying degrees of freedom. The main focus is on the principles of maximum entropy and maximum entropy production, and their application to biological problems across a wide range of scales - from understanding the evolutionary optimization of biologically important macromolecules to identifying the key determinants of species diversity in ecological communities.
Donc je pense que l’on reste dans le sujet.
PS. Cette théorie serait remise en cause.

[Sethy]

Reconnais que c'est la juste une affirmation.

Y a-t-il un résultat tangible, un avancée ou au contraire la preuve qu'une autre théorie est fausse ?

Si on prend les résultats de Prigogine par exemple, il explique la notion de bifurcation qui effectivement se retrouve dans l'expérience des cellules de Bénard. Expérience pour laquelle il y a une formule qui permet de déterminer le point critique au-delà duquel la bifurcation est probable et en dessous duquel elle est impossible.

Voici une vidéo qui explique justement la formule du seuil critique en question : https://www.youtube.com/watch?v=gSTNxS96fRg

[yvon l]

Quand je fais du cacao chaud, quand cela bout on n'a aussi apparition de cellule du type "benard"
En physique industriel il y a plein de formule de ce genre. Par exemple le passage d'un écoulement laminaire à un écoulement turbulent pour un liquide.
Je ne vois pas de quelle affirmation tu parles ?

[Sethy]

Quand je fais du cacao chaud, quand cela bout on n'a aussi apparition de cellule du type "benard"

Il y a de la convection, certes mais rien qui s'approche de structures hexagonales, relativement stable dans le temps. Il suffit de voir de l'eau qui bout, les bouillonnement évoluent sans cesse, se déplacent, etc. D'ailleurs pendant longtemps, l'expérience de Bénard constituait un paradoxe pour les physiciens qui peinaient à l'expliquer dans le cadre de la thermo classique.

En physique industriel il y a plein de formule de ce genre. Par exemple le passage d'un écoulement laminaire à un écoulement turbulent pour un liquide.

Il y a bien sûr tout une série de phénomène avec des seuils critiques. Toutes les bifurcations (au sens de Prigogine) présente ce seuil, mais tout phénomènes à seuil, n'est pas le résultat d'une bifurcation (au sens de Prigogine).

Je ne vois pas de quelle affirmation tu parles ?

Le texte en anglais du message #51. On y apprend que cette théorie trouve plein d'applications dans de nombreux domaines, mais ne renseigne en rien sur un phénomène inexpliqué qu'elle expliquerait.

[yvon l]

Voila le bon lien vers Dewar . Regardes l'onglet "recherche"
http://biology.anu.edu.au/people/roderick-dewar

[Sethy]

Discuter l'entropie pour elle-même est une «ornière» usuelle dans ce forum!

On s'est éloigné du sujet, le message #1 a mis en gras «La question porte sur la naissance de l'organisation dans les cellules vivante.»

Tu avais raison par "anticipation", mais j'ai essayé de recentrer le débat avec le message #48, qui propose un embryon de réponse.

[Sethy]

Si on suit cette logique, ça explique pourquoi il peut exister plusieurs espèces d'individus. Mais aussi, ça répond à la question initiale à savoir que certaines espèces ont pu cohabiter d'abord, coopérer ensuite pour donner lieu à des symbioses. Ou qu'une même cellule a pu donner plusieurs cellules filles qui en s'accolant et se spécialisant ont pu mieux utiliser le déséquilibre que ne le faisait l'espèce de la cellule mère seule.

Ici évidemment, deux visions peuvent s'affronter, car j'ai parlé de possibilité d'évolution. En aucun cas je n'ai évoqué ni le chemin suivi, ni surtout ce qui a entrainé l'évolution. A mon sens (et pas qu'au mien, vous le verrez), il y a 2 attitudes possibles.

Soit une imagine qu'une fois la vie apparue, la suite n'est que l'oeuvre du hasard, sachant évidemment qu'il y avait moyen que l'essai soit transformé (en tout cas dans l'hypothèse que je propose où un seul type de système en raison de sa taille, d'autres contingences, ne pouvait pas à lui seul convertir tout le déséquilibre potentiel en entropie).

Soit au contraire, on imagine une "force" (attention, il n'y a rien de déiste ici) inhérente au système même conduise inexorablement à explorer l'ensemble des solutions possibles et à rendre l'évolution inéluctable.

Ce qui nous renvoie à l'essai de Jacques Monod "Le Hasard et la Nécessité", auquel a d'ailleurs répondu Prigogine dans son livre "La nouvelle Alliance".

[ecolami]

Bonsoir,
Après réflexion en considérant des systèmes dont l'entropie varie je remarque que cette variation peut s'accompagner pour une partie d'un gain en organisation.
Comme ce n'est pas bien clair je prends un exemple simple
++si on brule un combustible on peut ne récupérer que de la chaleur ou avec un dispositif adéquat récuperer aussi un TRAVAIL.++ Ici ce mot travail est à prendre dans un sens large donc c'est une forme d'énergie qui peut expliquer la naisssance et la complexification de l'organisation.
Autrement dit le principe d'entropie n'est pas contredit et c'est juste qu'une partie de l'énergie du système est employée a organiser.
Je ne sais pas si cette explication est valable, qu'en pensez ?
Ici le terme système décrit quelque chose qui passe d'un niveau d'énergie a un autre niveau (globalement) inférieur

[Sethy]

La question est intéressante, en fait il ne faut pas l'un ou l'autre, il faut les 3.

C'est à dire à la fois "consommer" de l'énergie qu'on trouve dans les aliments pour produire le travail (1ère part d'énergie) nécessaire au mouvement, à la digestion, à la reproduction, etc. On parle du catabolisme. Cette consommation n'ayant pas un rendement de 100%, il y a donc de l'énergie utile perdue sous forme de chaleur (2ème part d'énergie). Mais il faut aussi sans cesse réparer la machine (anabolisme) par l'ingestion de protéine, qu'on casse pendant la digestion en acide aminé, qui sont récupéré par l'organisme afin de reconstruire les protéines qui ont été détruites et transformées en urée. Et pour cela, il faut une 3ème part d'énergie.

Cette 3ème part renferme également le point de vue microscopique, c'est à dire que les différents solutés vont avoir tendance à se mélanger, il faut en permanence les séparer via par exemple des pompes à Sodium, des canaux, etc.

Puisque la tendance spontanée est au nivellement des différences (comme de l'eau chaude et de le froide donneront toujours et inéluctablement de l'eau tiède, comme le colorant qui se diffuse). Il faut en permanence lutter (à grand renfort d'énergie) contre cette disparition des gradients nécessaires à la vie (en gros qu'il y ait dans chaque compartiment de la cellule ou de l'organisme multicellulaire, les bonnes substances aux bons endroits).

Note : j'ai adopté le point de vue énergétique, mais la question d'entropie apparait en filigrane.

[curiossss]

Soit une imagine qu'une fois la vie apparue, la suite n'est que l'oeuvre du hasard

Non. Pas que du hasard. La principale force évolutive est la compétition pour les ressources. Une espèce n'évolue pas toute seule, elle est interdépendante de son milieu, de ses proies et de ses prédateurs. Le hasard est à tous les niveaux, mais la loi des grands nombres fait que finalement il est un peu lissé. Ce qui se passe à l'extérieur d'une espèce joue autant sinon plus dans sa destinée que ce qui se passe en son sein (mutations, etc...).

Un spécialiste maîtrisant parfaitement tous les paramètres (une vue de l'esprit) pourrait prédire avec une bonne probabilité de réussite la destinée de toutes les espèces vivant actuellement. Donc pas autant de hasard que ça...

Un petit poisson à deux nageoires s'est adressé un jour à un gros poisson à quatre nageoires : "Monsieur, vous me semblez inutilement compliqué, toutes ces nageoires et toutes ces dents, au nom de l'Entropie je vous somme de me laisser ce vermisseau, car je meurs de faim !". Le gros poisson violant les lois de l'Entropie a pourtant eu plus de descendance que le petit poisson... La Fontaine aurait trouvé une morale pour cette histoire.