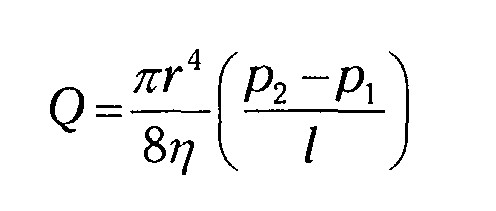Le débit de Poiseuille et les noces de Cana

[soliris]

Bonjour,

Il y a eu beaucoup de tentatives pour évaluer (avant Poiseuille) les pertes de charge (de pression P entre 2 sections distantes d'une longueur L) dans les "courants" de liquide à l'intérieur de canalisations.. courants qui sortent en "débits Q" .



Mais Poiseuille donne une solution intéressante (avec sa viscosité "êta") qui est parfaite au niveau des dimensions.. mais qui ne manque pas de poser des questions. D'un côté, la formule nous dit que la longueur L intervient à contresens (au dénominateur mathématiquement): normal: plus le tuyau est long, plus il y a de résistance à l'écoulement, moins le débit est grand à l'arrivée.

Mais la viscosité se trouve également au dénominateur; ce qui nous oblige à penser qu'il parle plutôt de fluidité (son inverse) au numérateur !
Ben quoi, ça a l'air normal, me direz-vous.. Pourtant c'est complètement différent, puisqu'elle intervient sur la longueur dont nous venons de parler.

Prenons la comparaison avec la chimie: la formule de l'eau est H₂O, or si nous mélangeons de l'oxygène et de l'hydrogène, nous n'obtenons pas de l'eau. En réalité, il faut brûler les gaz ensemble pour obtenir de l'eau. Pareillement, il ne suffit pas d'avoir une DDP dans un tuyau, même s'il y a du liquide, pour obtenir un débit. Il faut que les 2 ouvertures soient ouvertes, une à chaque extrémité. Sinon le liquide cesse très rapidement de couler..

L'idée à la base de cette analyse, c'est : pourquoi faut-il nécessairement une canalisation entre les 2 ouvertures ? Car la fluidité sans cette canalisation deviendrait maximale, et le liquide pourrait provenir de n'importe où .. Ce qui fait penser aux noces de Cana, ou à Moïse frappant sur le rocher pour obtenir de l'eau.

En quoi ai-je fait une erreur dans mon analyse ?
-----

[FC05]

C'est une loi qui permet de tenir compte (dans certaines conditions bien précises) des pertes de charge régulières dans un tuyau.

Bien entendu ça dépend de la longueur du tuyau (plus c'est long plus ça frotte) et de la viscosité (plus c'est visqueux et plus ça frotte).

Et là tu nous parle de fluidité et tu supprimes le tuyau !
Je te laisse faire la conclusion.

[albanxiii]

En quoi ai-je fait une erreur dans mon analyse ?

Vous faites parler les morts.

ce qui nous oblige à penser qu'il parle plutôt de fluidité (son inverse) au numérateur !

Vous comparez l'écoulement d'un fluide dans une conduite à la synthèse de l'eau. Et pour finir voir message #2.

On va donc arrêter le n'importe quoi.

albanxiii, pour la modération.