Electromagnétisme - Courant induit

[lepzorki]

Bonjour,

Un exercice sur le champ magnétique et le courant induit m'est proposé mais je rencontre quelques difficultés.

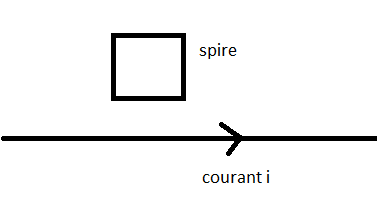
Enoncé 1: Dans un plan, une spire conductrice fermée se déplace parallèlement à un fil infini parcouru par i (voir schéma) Qu'observe-t-on dans la spire ?
J'aurai tendance à dire que la spire ne s'éloigne jamais du fil puisque elle se déplace parallèlement à celui-ci
Ainsi on observe aucune variation du champ magnétique B dans la spire donc pas de courant induit créé

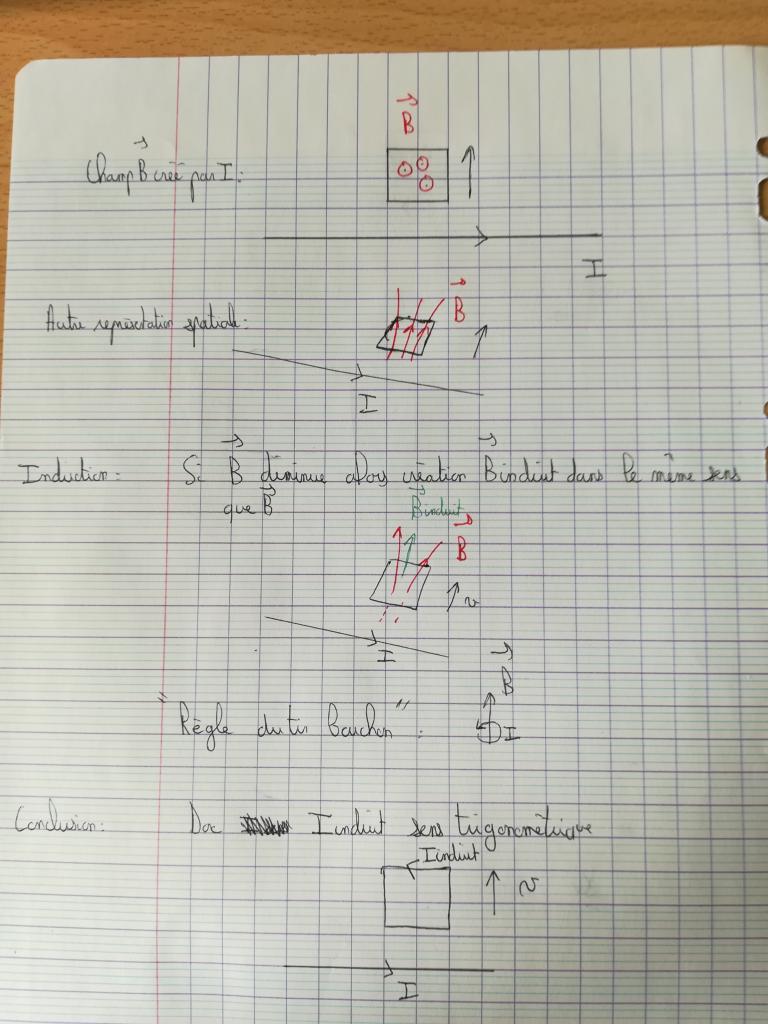
Enoncé 2: Dans un plan spire conductrice fermée est parallèle à un fil i. On coupe le courant d'un coup, que se passe-t-il ? (dans ce cas, la spire ne se déplace pas)
Je ne trouve aucun élément de réponse, j'aurai tendance à dire qu'il n'y a pas d'induction et pas de courant dans la spire mais je ne suis pas sur du tout

Pouvez-vous svp, m'éclairer pour ces 2 questions ?
Merci bcp d'avance

-----

[zTony]

Bonjour,

Tout d'abord, un petit rappel.
Il existe un courant induit s'il y a une variation du flux du champ à travers la spire.
Je rappelle que le flux du champ à travers la spire est définie par :
définie au signe près selon l'orientation choisie pour la spire.

Le fait de choisir un fil infini n'est probablement pas anodin : tu peux raisonner "simplement". A partir des symétries et des invariances, je te suggère de déterminer le sens et la dépendance du champ .
Cela te permettra de justifier plus proprement ta question 1 en raisonnant sur le flux du champ à travers la spire.

Pour la question 2, que se passe-t-il pour le flux du champ , si le champ est arrêté brutalement ?

Bonne journée,
zTony

[lepzorki]

Bonjour,

Merci pour votre réponse j'avais en effet compris que le champ est contenu dans les plans d'anti-symétrie de distribution du courant
Pour la question 2, si le champ est arrêté brutalement alors il n'y a plus de courant induit donc plus d'induction dans la spire ?

Merci

[zTony]

Bonjour,
L'énoncé 2 ne s'intéresse pas au courant induit après la coupure du courant, mais au courant induit entre le moment où il y avait un champ (avant la coupure du courant), et le moment où il y en a plus (après la coupure).
La question est donc : la coupure du courant provoque-t-elle un courant induit ?

[A voir en vidéo sur Futura]

[lepzorki]

Bonjour
Je ne sais pas quoi vous répondre mais si le champ disparaît il ya une variation puisque le champ diminue jusqu'à 0 Tesla donc un courant est créé ??

[zTony]

Bonsoir lepzorki,
c'est parfaitement ça : varie donc le flux varie, ce qui crée un courant induit.
C'est bien la variation du flux du champ qui crée ce courant (et non l'existence d'un flux nul ou non nul).


Pour information, d'après la loi de Lenz-Faraday, tout se passe comme s'il y avait une force-électromotrice (en convention "générateur") dans la spire.
Si vous avez encore des questions, n'hésitez pas.

Bonne soirée,
zTony

[zTony]

(Bien sûr, le courant induit disparaît rapidement par la suite, puisque le flux ne varie plus)

[lepzorki]

Donc pour résumer, quand on dit qu'on coupe brusquement le courant, on peut dire qu'il y a une variation de champ magnétique ?

Merci pour votre réponse

[zTony]

Oui.

Il est possible de calculer le champ produit pas un fil infini à l'aide du théorème d'ampère : l'unique composante du champ (orthoradiale, c'est-à-dire suivant ) est proportionnelle au courant I qui traverse le fil infini.
(théorème d'ampère --> 2nd année de classe préparatoire / licence a priori)

Bonne journée
zTony

[lepzorki]

Bonjour,

Très bien merci, je n'ai pas encore vu ce théorème mais ça va venir je pense
Simplement pour revenir à ma question, comme le champ diminue brutalement, peut-on dire que le courant induit dans la spire va circuler dans le sens horaire ? merci

PS : j'avais une 2nd question si ca ne vous dérange pas, j'ai vu que lorsqu'on approche un aimant d'une spire avec le pôle Nord orienté vers la spire, un courant induit dans la sens trigonométrique est créé,
est-ce que si j'approche l'aimant de la spire mais cette fois-ci avec le pole Sud orienté vers la spire, cela signifie que le courant induit créé sera dans le sens horaire ?

Merci encore,

[lepzorki]

En fait j'ai trouvé ce que je ne comprenais pas :
On se trouve dans le même cas que le schéma ci-dessus mais cette fois-ci la spire s'éloigne du fil.
Ce que je ne comprends pas est dans quel sans (trigonométrique ou horaire) va se déplacer le courant.

Si la spire s'éloigne du courant, le champ B va diminuer donc un courant induit va apparaitre qui va donner naissance à un champ Binduit.
Mais je ne peux pas appliquer "la règle du tir bouchon" car je ne sais pas dans quel sens est orienté le champ B.

Comme le champ magnétique est orthogonal aux symétries de courant, je dirai que B est orthogonal à l'écran de notre ordinateur mais je ne sais pas si il va vers moi ou vers l'opposé.

PS : en réalité il y a 2 plans orthogonaux de symétrie du courant, je ne sais pas quoi faire

[zTony]

Bonsoir,

je te propose 2 modes de raisonnement :
-par la loi de Lenz : dans ton cas : "le courant induit a un sens qui s'oppose à la variation de flux" (le champ induit et inducteur sont eux aussi opposés)
- Plus "rigoureusement" on peut utiliser la loi de Faraday :
1. Choisir une orientation du circuit. L'orientation du circuit fixe le sens du courant (mais pas son signe)
2. Exprimer le flux du champ magnétique (même si on ne peut pas l'exprimer clairement)
3. Exprimer la fém (force électromotrice) équivalente placée en convention générateur (c'est-à-dire que cela fixe le signe du courant) par la loi de Faraday :
4. Dessiner le circuit équivalent (sans oublier la petite résistance car un fil est toujours résistif)
5. grâce au signe de e, on en déduit le signe de i (et donc le sens qu'on aurait du choisir tel qu'il soit positif).

En réalité, la loi de Lenz est une conséquence de la loi de Faraday.


Si l'une ou les deux méthode(s) ne te semblent pas claires, n'hésite pas à me le dire, je détaillerai.

Bonne soirée,
zTony

[lepzorki]

Bonjour,
merci pour la réponse mais je ne trouve toujours pas la solution à mon problème

En fait je n'arrive pas à visualiser le champ induit créé par le courant I dans le fil

je suis censé résoudre ce problème sans calcul, simplement en ayant compris le cours

[lepzorki]

voila ce que je propose

[zTony]

Oui c'est bien la bonne réponse !

Je rajoute une couche (au cas où, même si je pense que tu as complètement compris)
Le courant induit s'oppose à la diminution du flux (cause qui a donné naissance au courant) puisque le champ induit est, d'après la "règle du tir bouchon", dans le même sens que le champ inducteur [qui diminue].
Dans cette logique, si le champ inducteur augmentait, pour s'opposer à l'augmentation du flux à travers la spire, il faudrait un champ et donc un courant de sens contraire par rapport au cas précédent.

[lepzorki]

Merci pour la réponse,
Il reste une chose floue pour moi, ici le courant du fil I "va vers la droite" donc le le champ B créé par I tourne dans un certain sens avec la règle du tir bouchon
Est-ce que si le courant allait "vers la gauche" alors le champ B tournerait dans l'autre sens ? (encore une fois avec la règle du tir bouchon)

D'une manière plus générale, quand on fait la règle du tir bouchon, est-ce que dans un cas on peut prendre notre pouce comme le champ B, et dans d'autre cas notre pouce comme le courant I ?

Merci encore,

[zTony]

Bonjour,

Oui, si le courant tournait dans l'autre sens, alors le sens du champ serait inversé, car on doit retourner le pouce dans la "règle du tir bouchon" (et cela s'exprime bien sûr à l'aide d'équations, de manière analytique !!)

La "règle du tir bouchon" (ou "règle de la main droite") est applicable dans les deux cas (en prenant le courant ou le champ [vec]\vec{B}[/tex] pour le pouce). Voici par exemple les lignes du champ d'une spire :
http://www.chimix.com/an11/concours1...es/itpe117.gif
Ainsi, cela marche :
- en prenant le pouce pour le champ créé sur l'axe de symétrie
- en prenant le pouce pour le courant dans la spire --> en parcourant avec le pouce la spire, on remarque que la contribution du champ est toujours du même sens et on peut se dire (qualitativement) qu'en sommant les différentes contributions de champ le long de la spire, on obtient un champ de tel sens

C'est une règle qualitative, qui permet d'avoir quelques "intuitions" sur les lignes de champ.

zTony

[lepzorki]

Merci énormément pour vos réponses, j'ai une dernière question de cours si ca ne vous derange pas :

Pour obtenir la forme locale de la loi d'Ampère dans le repère cartésien, que faut-il faire svp ?

Faut-il utiliser l'intégrale sur un contour rectangulaire et faire tendre vers quelquechose ou à travers une surface parallépipédique et faire tendre vers quelque chose?

Merci d'avance

[zTony]

Bonjour,

je ne parviens pas à comprendre votre question. De quoi souhaitez-vous partir pour obtenir la forme locale de la loi d'Ampère dans le repère cartésien ?
De la forme locale de la loi d'Ampère (ou "équation de Maxwell-Ampère") ?

Edit : je viens de voir la modification de votre message. Je comprend mieux. Je répond dans un prochain post

zTony

[lepzorki]

Dans un exercice de TD on me demande simplement comment obtenir la loi d'Ampère dans le repère cartésien à partir de la forme intégrale

[lepzorki]

On me propose d'appliquer l'intégrale à travers surface parallépipédique puis d'intégrer vers un rectangle ou un point
Ou alors d'intégrer sur un contour rectangulaire et faire tendre faire un point ou un rectangle

Je ne sais pas quelle affirmation est juste

[zTony]

Donc si j'ai bien compris tu souhaites passer de :

à :

(valable en régime statique ou dans l'approximation des régimes quasi-stationnaires)
Connais-tu le théorème de Stokes ( http://res-nlp.univ-lemans.fr/NLP_C_..._M07G01_5.html ) ?

Edit : je viens de voir la nouvelle modification du message : je vais adapter ma réponse

[zTony]

Re-bonjour,

Il faut faire les deux ! Chaque étape correspond à un côté de l'égalité :
On a :
On te demandes de montrer :


Je te proposes de partir avec un rectangle de sommets (x,y), (x+a,y), (x,y+b), (x+a,y+b)
1. Ecrire le théorème d'Ampère version intégrale.
2. Pour l'intégrale sur le contour, divise l'intégrale ("relation de Chasles") en 4 intégrales sur chaque segment. Attention au signe lors des projections de !!
3. Diviser par
4. Faire tendre a vers 0, puis b vers 0, en reconnaissant des dérivées.

Notamment, on peut exprimer

Bonne chance
zTony

[lepzorki]

Merci beaucoup pour ces détails !

Pour résumer la méthode, il faut intégrer sur un rectangle (par exemple de longueur/largeur a/b) puis faire tendre a et b vers 0 donc faire tendre vers un point
et on obtient en coordonnées cartésiens

C'est cela ?

En fait j'ai un doute : on intègre sur un contour rectangulaire ou une surface parallépipédique ?

merci encore,

[zTony]

Oui c'est bien ça. Vous obtenez alors la forme locale en (x,y,z), le fameux point.
(D'ailleurs, lors de la démonstration, il faut bien préciser , sinon il risque d'avoir des erreurs.)

[lepzorki]

D'accord merci, donc a et b représentent le contour d'un rectangle et non la surface d'un parallépipède ?

merci

[zTony]

Oui, c'est bien d'un rectangle, désolé, j'ai vraiment lu de travers !
Ha oui, je n'avais pas vu "surface parallélépipédique" dans ton ancien message ! J'avoue que je ne vois pas trop l'intérêt pour la surface parallélépipédique !
Donc, excuse-moi, il ne faut pas faire comme je l'avais dit, utiliser les deux "méthodes", c'est bien soit l'un, soit l'autre.
Et il me semble que le rectangle soit plus adapté car il n'y a que des intégrales surfacique ou linéique.

Encore désolé ^^
zTony

[lepzorki]

Très bien
merci infiniment pour vos réponses ça m'a vraiment aidé car je ne trouvais pas les infos

[zTony]

C'est un vrai plaisir
zTony