Bonsoir,
Pour un fluide thermo-visqueux l'équation de propagation des ondes acoustique est :
avec b un coefficient positif caractérisant l'absorption
il nous demande de démontrer la relation de dispersion de ce fluide, et je sais vraiment pas comment faire. Merci pour votre aide
D'après le nom (je crois comme pour les ondes....) , c'est que
la somme de tous donne la relation de dispersion:
ps: tous ça, c'est par analogie avec l'équation des ondes (à toi de voir le cours...)
pfffEnvoyé par azizovsky
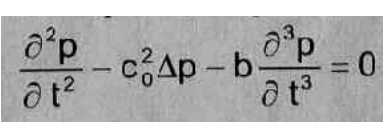
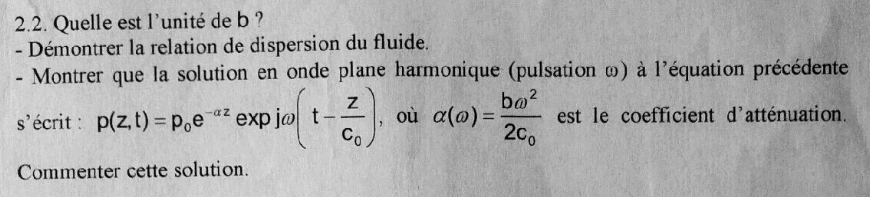Merci pour ton réponse , mais cette solution ce n'est pas plutôt pour l'acoustique linéaire. parce que après cette question il nous demande de montrer que ceci :est la solution de l'équation.
Bonjour, je ''sais'' que ce n'est pas linéaire (facteur d'amortissement...) , mais la méthode reste la même ....(rentrer la solution dans l'équation....)
Bonjour,
d'accord, mais pourquoi il nous demande de montrer que la solution proposé est le bon ?
C'est un domaine un peu compliqué, voir par exemple : https://pastel.archives-ouvertes.fr/...se_X_Jacob.pdf
la solution est solution de l'équation de Burgers*, qui est la version unidimensionnelle de celle de Westervelt , et l'équation de l'exercice est celle qui vérifie la pression en 1ère approximation p(1) avec (p=M.p(1)+M².p(2)) (M: nbr de mach)
la méthode que j'ai donné, est utilisé par exemple ici http://modb.oce.ulg.ac.be/cours/MECA...053-2notes.pdf
onde de Poincaré ,Kelvin,... Rossby,
* https://fr.wikipedia.org/wiki/%C3%89quation_de_Burgers
