Bonjour,
Voici ce que j'ai pu trouver dans un cours sur le traitement du signal au sujet de la quantification analogique -> numérique :
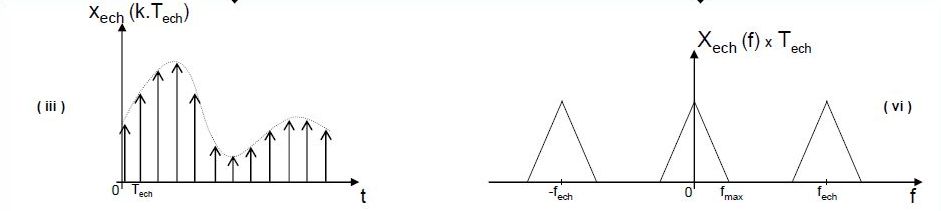
Je ne comprends pas comment l'auteur peut, à partir de l'eq 3.1, dessiner le spectre en fréquentiel...
D'avance merci pour votre aide.
AK
Bonjour,
Euh... quelles sont les fréquences présentes dans le signal donné par l'équation 3.1 ?
Not only is it not right, it's not even wrong!
Salut,
l'equation 3.1 te decompose ton signal periodique dans une base (de dimension infinie) de sinus et cosinus, concretement ca veut veut dire que le signal x(t) vaut sensiblement: une valeur moyenne a0 et une somme infinie de differentes harmoniques de sinus et cosinus qui sont toutes ponderees par des constantes (les an et les bn).
NB: Ce que j'appelle harmonique ici est un cos (ou sin) dont la frequence est un multiple de la frequence de base. Exemple: Si on a s(t)=cos(Ft)+3cos(2Ft)+2cos(5F t), j'appelle les 3 fonctions cos(Ft), 3cos(2Ft) et 2cos(5Ft) des harmonique de s(t) (La premiere harmonique cos(Ft) est aussi appellee fondamental).
Donc on peut dire que x(t) est une addition de plein de fonctions sin et cos (ponderees et de frequences multiples d'une frequence de base F), ainsi que d'une valeur moyenne constante (qui peut etre vu comme un cos de frequence nulle).
Dans ton cas donner les spectres en cos et sin de x(t) ca signifie indiquer ces fonctions (poids et frequences) qui compose x(t) dans deux graphes, ca c'est la decomposition en serie de Fourier qui nous le donne (3.1).
Pour le spectre en cos, on regarde que la partie qui contient les cos la decomposition de x(t)
Avec cette ecriture faut faire attention a pas oublier que a0 a pas les meme expression que les an pour n non nul.
Le graphe du spectre en cos sert juste a caracteriser les harmoniques, tu places en ordonnee le poids de l'harmonique (son amplitude) et ordonnee sa frequence (qui est donc toujours un multiples d'une frequence de base, ici Fp).
NB: Donc a chaque point (ou trait ou impulsion, tu le vois comme tu veux) du spectre correspond une fonction a.cos(n.F.t) de duree infinie, qui compose ton signal de depart.
Evidement c'est la meme chose pour le spectre en sin.
Deso si j'ai ecrit ecrit des trucs evidents ou que j'ai tourne autour du pot, j'espere en tout cas avoir aide.
Il manque evidemment des 2pi dans les cos et sin.
Bonjour :
a) pour abanxii :
C'est évident :
b) pour Igen :
Merci beaucoup.
- J'ai un peu cogité : je voulais absolument écrire
- D'autre part, si on multiplie
Dans le cas general, c'est vrai. Il existe un cas où le signal echantillonne (signal de depart multiplie par un peigne de dirac) a une periode finie (la meme que celle du signal continu de depart), c'est lorsque l'espace entre les diracs, Te, est un multiple de la periode du signal continue.si on multiplie par un peigne de Dirac, on obtient un signal périodique à l'infini, n'est-ce pas ?
NB: Attention a respecter Shannon (Fe>2Fmax) sans quoi y a du repliement spectral, ce qui revient a perdre de l'information, on peut plus retrouver le signal de depart a partir de l'echantillonne.
On utilise une transformee de Fourier cependant c'est la version discrete, la TFD, qui devrait etre utilise ici.Et là il faut utiliser non pas les séries de Fourrier, mais la transformée
NB: La TFD a la particularité de ne considerer qu'un morceau d'une longueur finie dans le temps d'un signal numerique, a la difference de la TF qui permet de considerer un signal continu sur un duree de temps infinie. La TFD, elle va naturellement considerer qu'en dehors ce morceau de signal analyser le signal se repete, autrement dit, elle va periodiser (en temporel) ce morceau de signal analyse et retourner le spectre discret de ce signal periodise.
Donc pour avoir un bon spectre de ton signal continue (bien representatif) t'as tout interet à:
-choisir une periode Te multiple de la periode du signal continu T.
-respecter Shannon
-appliquer la TFD a une periode de ton signal echantillonne (si tu prend une periode, le fait que la TFD periodise le morceau de signal analyse n'est pas un probleme vu que ce morceau est une periode si elle est periodise ca reste exactement egal a l'echantillonne complet de depart. C'est pourquoi on l'utilise la TFD sur des signaux periodiques)
NB2: Si tu veux traiter des signaux echantillonee aperiodique faudrait plutot se tourner vers la transformee en z.
Alors si je comprend bien ce dont tu parles, tu vois le passage du spectre discret d'un signal periodique continu (serie de Fourier) a un spectre continue qui serait le resultat d'un signal aperiodique continu auxquel on aurait applique une transformee de Fourier, en partant du principe qu'un signal aperiodique est un signal periodique de periode infinie.du coup on trouve des aires (ayant la valeur des intégrales) centrées sur les fréquences du fondamental et des harmoniques. Exact ?
De mon point l'image ne marche pas, ce ne sont pas ces types de signaux que l'on manipule ici (nos signaux sont discrets, pas continus).
Dans notre cas on utiliserez plutot la TFD car le signal est discret et periodique (si le peine de dirac bien choisi cad Te multiple de T) sinon une TZ car le signal serait discret et aperiodique.
Dans les deux cas le spectre est aussi discret donc il n'y a pas d'aire mais encore des traits.
Il y a beaucoup de differentes transformation pour analyser les signaux, je te conseille ce passage d'une video tres utile qui recapitule les differents cas d'utilisations des transformees et quelques proprietes à savoir (le reste de la video est aussi tres interessante mais c'est un poil long)
https://youtu.be/tmVfRYt7Fss?t=878
Deso pour les eventuelles fautes d'orthographe.
Cliquez pour afficher
Bonsoir Igen, et merci pour ton aide.
Non, je me suis mal exprimé, ce que je voulais dire c'est comment on passe de la fig III à la fig VI ci-dessous ?
A gauche on part d'un non périodique (ou périodique à l'infini) on multiplie par un peigne de dirac (de période T permettant de respecter shannon) et on obtient III, à droite on fait une convolution dans le domaine fréquentiel (avec un peigne de F = 1/T) et on obtient VI.
Ce que je ne sais pas c'est comment on représente graphiquement les spectres continus représentés sur VI. On a l'habitude de faire des triangles équilatéraux avec je suppose comme "enveloppe" l'ensemble des max des amplitudes des raies obtenues en temporel, mais bon... Ca sort d'où que c'est des triangles ? On pourrait très bien avoir une enveloppe qui ressemble à une gaussienne par ex... Non ? Ou alors je passe à côté d'une évidence du genre : comme le signal est périodique à l'infini mais avec une fréquence max, ben toutes les fréquences entre 0 et Fmax sont présentes...
Te presse pas pour répondre c'est pas super urgent.
A+
AK
Ah desole, j'etais loin de ta question.
J'espere que ca va pas te decevoir mais ca vient du fait qu'un traiteur du signal reflechie davantage comme un physicien que comme un mathematicien. Ces triangles representent le spectre (TFDT) d'un signal numerique (le spectre d'un signal discret est continu vu que, comme tu l'as ecrit, il s'agit du spectre du signal continu convolue par des diracs) ou encore l'enveloppe de la TFD de ce meme signal. Il s'agit d'une representation tres approximative de la forme, dans l'absolue on aurait, par exemple, pu choisir de representer ca par une porte, ce qui aurait voulu dire que le signal a autant d'energie a toutes les frequences, or c'est pas le cas le plus courant. Souvent les harmoniques haute frequence portent moins d'energie que celles basse frequence, la forme triangle represente pas trop mal cela.On a l'habitude de faire des triangles équilatéraux avec je suppose comme "enveloppe" l'ensemble des max des amplitudes des raies obtenues en temporel, mais bon... Ca sort d'où que c'est des triangles ?
NB: La TFDT (Transformee de Fourier Discrete Temporelle) prend un signal echantillonne et retourne son spectre continue. La tranformee dont je parlais plus tot, la TFD, est en realite un echantillonne de la TFDT.
Cliquez pour afficher
Dans de nombreux cas, la forme exacte du spectre n'est pas tres importante, on va davantage s'interesser a la frequence max et a l'evolution globale des amplitudes des harmoniques.
Ah et le fait que le triangle soit isocele vient du fait que le spectre d'un signal reel (c'est quasiment toujours le cas) est symetrique (autour des axes verticaux d'abscisse f=n.fe, pour tout n entier relatif).
Un signal mesure avec capteur admettra toujours une frequence max. Des lors qu'on manipule des signaux non continus comme des portes ou des diracs on a des spectres infinis (sinus cardinal, constante).Ou alors je passe à côté d'une évidence du genre : comme le signal est périodique à l'infini mais avec une fréquence max, ben toutes les fréquences entre 0 et Fmax sont présentes...
Cependant en pratique quand on veut pas de probleme, on utilise SYSTEMATIQUEMENT un filtre passe bas (filtre antirepliment) avant d'appliquer une transformee afin d'etre certain que la fmax du signal est inferieur a fe/2 (Shannon).
Bonjour Igen,
Ca commence à être plus clair, mais je dois encore travailler tout ça...
Merci beaucoup pour ton aide !
Bonne continuation.
AK
