Gravité locale

[Sethy]

C'est-à-dire, si j'ai bien compris, que la plume et le marteau tombent en même temps sur le sol de la lune, ...parce que leurs masses respectives, par rapport à celle de la lune, sont excessivement faibles, (ou pour le dire autrement, leurs masses respectives sont infimes "relativement" à la masse de la lune),
merci.

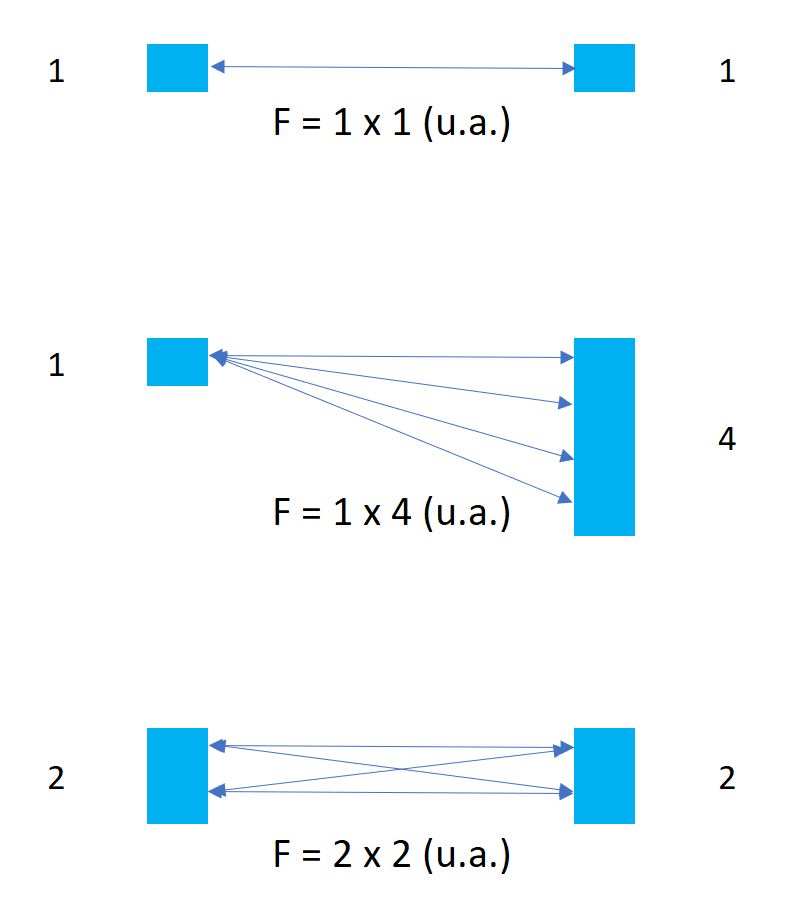
Pour moi, le plus important est que l'accélération initiale subie tant par la plume que par le marteau sont exactement les mêmes.

Et cela se montre si on se rappelle que (m minuscule est l'objet, M majuscule la masse de la Lune) :

1/ F = m . a
2/ F = - G . m . M / r^2

Si on égale les forces, il vient :

m . a = - G . m . M / r^2

Simplifions par m :

a = - G . M / r^2

Donc m, la masse de l'objet disparait complétement de l'expression de l'accélération initiale qui ne dépend que de la masse de la Lune et du "rayon".
-----

[coussin]

Rigoureusement parlant, il faut séparer le mouvement du centre de masse Lune-marteau. Après ça, l'équation à résoudre est F = mu . a avec mu = mM/(m+M) la masse réduite.
Seulement si M>>m on peut approximer mu par m et vos équations ci-dessus sont correctes.

[Sethy]

Rigoureusement parlant, il faut séparer le mouvement du centre de masse Lune-marteau. Après ça, l'équation à résoudre est F = mu . a avec mu = mM/(m+M) la masse réduite.
Seulement si M>>m on peut approximer mu par m et vos équations ci-dessus sont correctes.

Bien sûr. Mais tout aussi rigoureusement parlant, l'accélération initiale telle que je la décris est correcte (merci de confirmer) ?

(On se place clairement dans la physique de Newton bien sûr)

[coussin]

Bien sûr. Mais tout aussi rigoureusement parlant, l'accélération initiale telle que je la décris est correcte (merci de confirmer) ?

(On se place clairement dans la physique de Newton bien sûr)

Oui et non...
Repartons de zéro. Dans le système d'un marteau (de masse m) et la Lune (de masse M) en interaction gravitationnelle, on a à résoudre un système d'équations différentielles couplées

avec le vecteur position du marteau, le vecteur position de la Lune et (je prends des libertés avec les vecteurs etc par souci de simplicité...).
Ce que vous dites, et qui est vrai, c'est que je peux simplifier la première équation de ce système par . Ainsi, ne dépend plus de , certes.
Mais ce n'est que la moitié du problème. Ce qui nous intéresse est la quantité et une équation différentielle pour cette quantité est obtenue en séparant la mouvement du centre de masse (ce qui revient simplement à additionner et soustraire les 2 équations différentielles) et fait alors apparaître la masse réduite.

[franklin.]

Bonjour,

Maintenant si la question est de savoir si la courbure générée par deux masses* identiques (50-50) est rigoureusement la même que la courbure générée par 2 masses différentes (75-25) la réponse est non en toute rigueur. Mais suivant le problème étudié, soit cela à une importance, soit aucune.

je me permets de revenir une nouvelle fois sur cette discussion ;
il me semble justement que dans ce cas précis, cela a une importance. En effet au cours du fil de discussion, vous relevez que la force gravitationnelle est de loin la plus faible de toutes les forces. Oui, je ne peux que l'admettre (en l'état actuel).
Mais ce qui m'intrigue ou me pose question, c'est que devient l'intensité de cette force en présence de deux objets de masse absolument équivalente (deux protons par exemple), notamment la question porte sur la force qu'exerce l'un sur l'autre ces deux objets ?
En espérant que cette question a un sens?

(J'ajoute à nouveau, si c'est nécessaire, que la fameuse expérience de Neil Armstrong vérifiant le principe d'équivalence faible illustre l'exercice de la force gravitationnelle à grande échelle (au niveau macro), mais pas à petite échelle (au niveau micro). Or au niveau d'échelle micro, nous ne sommes pas en présence d'objets ayant une masse nécessairement négligeable par rapport à la masse d'un autre objet, comme par exemple un marteau (ou encore une plume) par rapport à la masse de la lune (à laquelle il faut ajouter une atmosphère extrêmement ténue pour valider l'expérience).

A cette échelle (micro), les objets considérés peuvent avoir une masse exactement égale, je suppose ou j'imagine alors que la force gravitationnelle en jeu est beaucoup moins négligeable.

Enfin j'interroge non seulement l'influence des masses égales, il faut peut-être aussi ajouter celle des distances infimes, mais c'est encore une autre question.

En espérant que cette intervention ne me fasse pas paraître buté.

Merci grandement.

[coussin]

Pour la part, je n'ai rien de plus à ajouter sur ce sujet.

Je ne comprends pas pourquoi vous vous intéressez au cas de l'interaction gravitationnelle entre 2 masses égales comme si c'était un cas spécial ou particulier... Les équations différentielles couplées à résoudre que j'ai donnée dans mon dernier message sont les mêmes quelles que soient les masses en jeu.

Au niveau microscopique, la validité de la force de gravitation est testée grâce à des expériences de type Casimir. En effet, l'intensité de l'interaction de Casimir peut devenir de l'ordre de l'interaction gravitationnelle pour des objets de taille micrométriques séparés par des distances, elles aussi, de l'ordre du micron.

[Sethy]

Imaginons quelque chose de très proches, disons 2 charges électriques égales mais de signe contraire.

Elles s'attirent l'une l'autre. La situation où les deux masses sont rigoureusement identique, ne diffère pas fondamentalement de celle où la masse d'une des deux particules est double de l'autre. La rencontre ne se fera pas au "milieu" (hypothèse des deux masses ayant une vitesse nulle initiale), mais sera déplacée vers la masse la plus lourde et ce d'autant plus que le rapport des masses (lourde / légère) est important.

[Deedee81]

Salut,

Petit coup de pouce sur ça.

vous relevez que la force gravitationnelle est de loin la plus faible de toutes les forces. Oui, je ne peux que l'admettre (en l'état actuel).

C'est très facile à constater. Prend un petit copeau de fer. Place un aimant au-dessus .... hop il se soulève. Le copeau est attiré par une planète entière (six mille milliards de milliards de tonnes) et par un cht'tit aimant : qui gagne ?

La force de gravité n'est pas du tout négligeable car elle a le bon goût d'être toujours attractive. Et l'énergie résultant de l'accrétion est importante pour des corps énormes (une étoile brilles plusieurs millions d'années à sa naissance avant même que le thermonucléaire prenne le relais, c'est dû à l'échauffement dû à la compression à cause du poids). Mais le fait que cette interaction fasse minable par rapport aux forces EM est clair comme de l'eau de roche (et donc aussi évident par rapport aux interactions nucléaires..... plus difficile à voir par soi-même par rapport à l'interaction faible)

[coussin]

Rendez-vous dans quelques mois pour la suite de ce sujet

[Nicophil]

vous relevez que la force gravitationnelle est de loin la plus faible de toutes les forces. Oui, je ne peux que l'admettre (en l'état actuel).

À l'échelle cosmologique ? NON

Certes, l'expansion est accélérée, mais seulement depuis 1998 (enfin, j'me comprends) !

[franklin.]

Bonjour,

Je ne comprends pas pourquoi vous vous intéressez au cas de l'interaction gravitationnelle entre 2 masses égales comme si c'était un cas spécial ou particulier... .

"m_p: masse du proton en kg (elle apparaît au carré !)" citation de ThM55 (dans la discussion fermée).

(j'ai pu, avec l'accord de Deedee81, reprendre cette discussion relativement similaire à celle fermée récemment :
dont le titre était : Noyaux des atomes et "gravité locale" ?)

Vous me pardonnerez, j'espère, ma naïveté due à une non compétence certaine (que j'essaie progressivement de combler).

En faisant abstraction de la comparaison de l'intensité des forces, je souhaitais quand même répondre à cette question de coussin ;

je m'intéresse à ce cas d'interaction gravitationnelle entre 2 objets de masses égales (les protons ici) car, en espérant ne pas faire du "gloubiboulga", je m'interroge sur la courbure locale de l'espace. (Puisqu' il semble que la force gravitationnelle résulte de cette courbure).

La force gravitationnelle, exprimée dans le cas des masses égales, est donc dépendante du carré de cette même masse ; je m'interroge alors :
-la force (la courbure de l'espace donc ?), dans ce cas, semble donc s’exprimer comme une fonction dépendante d'une masse élevée au carré ;
-la courbure locale de l'espace (temps ?) est-elle alors de forme parabolique ? (à cause de l'élévation de cette masse au carrée comme le précise Thm55),
-si oui, cette courbure peut-elle alors agir comme une sorte de "puits gravitationnel" entre les
2 protons ?

(Désolé si mon intervention sort des clous de la charte, ou si elle complètement absurde, illogique et non-scientifique, mais je voulais juste pouvoir clore cette interrogation...)

Merci à la bienveillance de Deedee81. (Dans l'attente d'une réponse, ou d'une fermeture de la discussion si il y a lieu).

Cordialement,
franklin

[Archi3]

La force gravitationnelle, exprimée dans le cas des masses égales, est donc dépendante du carré de cette même masse ; je m'interroge alors :
-la courbure de l'espace, dans ce cas, semble donc s’exprimer comme une fonction dépendante d'une masse élevée au carré ;
-la courbure locale de l'espace (temps ?) est-elle alors de forme parabolique ? (à cause de l'élévation de cette masse au carrée comme le précise Thm55),

mais si tu regarde un carré, ce n'est pas courbe, c'est droit avec des angles. Donc à mon avis la courbure est faite de petits segments de droite séparés par des angles, tu crois pas ?

[mach3]

La force gravitationnelle, exprimée dans le cas des masses égales, est donc dépendante du carré de cette même masse ; je m'interroge alors :
-la force (la courbure de l'espace donc ?), dans ce cas, semble donc s’exprimer comme une fonction dépendante d'une masse élevée au carré ;
-la courbure locale de l'espace (temps ?) est-elle alors de forme parabolique ? (à cause de l'élévation de cette masse au carrée comme le précise Thm55),
-si oui, cette courbure peut-elle alors agir comme une sorte de "puits gravitationnel" entre les
2 protons ?

C'est complétement dans les choux hélas.
La courbure de l'espace-temps ce n'est pas du tout ce qu'on peut s'imaginer en lisant la vulgarisation et en voyant des images de ce genre : https://fr.wikipedia.org/wiki/Espace..._curvature.png . Cela n'a quasiment rien à voir. Parler d'une forme parabolique est limite hors-sujet, et le lien entre la courbure de l'espace-temps et sa source (la masse oui, mais en fait tout ce qui est énergie et quantité de mouvement) est bien plus compliqué que ça. Les astres ne se déplacent pas comme des billes dans les cuvettes que font les autres astres et ces cuvettes ne sont pas un puits gravitationnel, ça ne marche pas du tout comme ça.
En plus dans le contexte de la RG (parce qu'on parle de courbure de l'espace-temps), la gravitation N'EST PAS une force.
Enfin, un proton possède une masse tellement faible que la gravitation est limite hors-sujet si on s'intéresse à son interaction avec un autre proton.

m@ch3

[franklin.]

Bonsoir,

C'est complétement dans les choux hélas.

Entendu.

La courbure de l'espace-temps ce n'est pas du tout ce qu'on peut s'imaginer en lisant la vulgarisation et en voyant des images de ce genre : https://fr.wikipedia.org/wiki/Espace..._curvature.png

Au moins, faudrait-il, pour pouvoir la représenter en 2D, la penser sous forme de vecteurs, j'imagine...

cordialement ;
franklin

[Deedee81]

Salut,

Au moins, faudrait-il, pour pouvoir la représenter en 2D, la penser sous forme de vecteurs, j'imagine...

Ca existe, la courbure intrinsèque est décrite par le tenseur de Riemann-Christoffel. Et les tenseurs sont des vecteurs.

Et la représenter est facile à 1D (là c'est même trivial, la courbure extrinsèque est le "rayon de courbure" comme pour les routes, et il n'y a pas de courbure intrinséque). A 2D c'est pas très difficile non plus (une seule composante intrinsèque et deux rayons de courbure). Mais à 3D edifficile et 4D un cauchemar. Le problème est que le nombre de "paramètres" augmente vite.

Ainsi à 4D le tenseur de courbure a 256 composantes, oui, 256 ! Dont 20 indépendantes. Et ça en chaque point d'un espace lui même à 4D. Donc on peut représenter certains cas simplifiés (très simplifiés) mais une représentation générale => impossible, sauf à se le représenter mentalement de manière abstraite, avec des équations (notre esprt a ses limites mais il reste assez bon pour les abstractions)

[coussin]

Sans rentrer dans des détails de calculs tensoriels, il y a une image intuitive de la courbure en 3D en tout cas : c'est la différence avec du volume d'une sphère de rayon R.
Ça n'a donc aucun lien avec une "forme parabolique". Au moins dans cette image simplifiée, c'est un nombre tout bêtement.

[Deedee81]

Sans rentrer dans des détails de calculs tensoriels, il y a une image intuitive de la courbure en 3D en tout cas : c'est la différence avec du volume d'une sphère de rayon R.
Ça n'a donc aucun lien avec une "forme parabolique". Au moins dans cette image simplifiée, c'est un nombre tout bêtement.

Tu veux parler des excès sphériques ? C'est vrai que c'est un moyen simple d'introduire le sujet. C'est ce que j'utilise dans mon introduction à la RG. S'il n'est pas possible d'avoir une représentation simple du cas général, il est tout à fait possible d'avoir une introduction progressive et intuitive au sujet... avant de plonger dans les abstractions calculatoires. Il y a des sujets très difficiles à vulgariser (comme le spin par exemple), mais en réfléchissant, en y allant pas à pas, ça prend pas mal de "lignes" mais on y arrive (même pourt le spin j'ai relevé le défit et j'ai une série vulgarisée complète sur le sujet).

[coussin]

Tu veux parler des excès sphériques ?

Hmm, je ne sais pas...
Je parle du scalaire de Ricci https://fr.m.wikipedia.org/wiki/Cour...ume_des_boules

[Deedee81]

C'est lié.

[franklin.]

Salut,



Ca existe, la courbure intrinsèque est décrite par le tenseur de Riemann-Christoffel. Et les tenseurs sont des vecteurs.

Et la représenter est facile à 1D (là c'est même trivial, la courbure extrinsèque est le "rayon de courbure" comme pour les routes, et il n'y a pas de courbure intrinséque). A 2D c'est pas très difficile non plus (une seule composante intrinsèque et deux rayons de courbure). Mais à 3D edifficile et 4D un cauchemar. Le problème est que le nombre de "paramètres" augmente vite.

Ainsi à 4D le tenseur de courbure a 256 composantes, oui, 256 ! Dont 20 indépendantes. Et ça en chaque point d'un espace lui même à 4D. Donc on peut représenter certains cas simplifiés (très simplifiés) mais une représentation générale => impossible, sauf à se le représenter mentalement de manière abstraite, avec des équations (notre esprt a ses limites mais il reste assez bon pour les abstractions)

Bonjour,
l'effet qu'exerce la masse d'un objet sur l'espace/temps n'est pas une "cuvette" (même si cela permet de se faire une idée visuelle vulgarisée) ;
j'imagine, qu'au moins en 3D, il faut penser cette effet comme un champ vectoriel se dirigeant vers le centre de cet objet (impossible à représenter visuellement dans cette dimension),
merci,
dans l'attente d'une réponse, si nécessaire

[franklin.]

mais si tu regarde un carré, ce n'est pas courbe, c'est droit avec des angles. Donc à mon avis la courbure est faite de petits segments de droite séparés par des angles, tu crois pas ?

Bonjour,

cette remarque me conduit à poser une question plus en relation avec les mathématiques, je ne sais pas si cette interrogation est logiquement valable ?

(en mettant de côté ici le questionnement concernant l'effet de la gravité sur la géométrie de l'espace-temps) ;

on a effectivement algébriquement un carré, mais :

- en géométrie "pure", euclidienne, un carré ne décrit -il pas la variation de la surface d'un carré, en fonction de la variation de la longueur de son côté ?
- en géométrie analytique, cette variation peut-elle être figurée par une parabole (en tous cas pour sa partie positive) ?

est-ce que je patauge complètement, ou ces questions ont-elle un sens (Peut-être en mathématiques ? Peut-être pas en physique ?) ?

Merci

[franklin.]

Bonjour,

je souhaite, après réflexion, poser une question avant tout, parmi d'autres,

- sans considérations de la différence de masses des protons par exemple, et de celle des objets macroscopiques, qui ont pu alimenter mes interventions,

- et en m'en tenant à l'équation décrivant la gravité universelle selon Newton,
soit : FA/B = G Ma*Mb/d²

en envisageant maintenant des valeurs arbitraires de masses,
- par exemple : Ma = 4kg et Mb = 1kg, on obtient que FA/B = 4G/d²
- puis on considère deux autres objets, A' et B', et on pose leur valeur, telle que : Ma'= 2 kg et Mb' = 2 kg, on obtient donc FA'/B' = 4G/d² aussi,
donc, on a bien : FA/B = FA'/B' (??)

pourtant cela ne me semble pas similaire,
- si on considère la valeur des "forces", sans doutes oui,
- mais pas du tout, en terme de vecteurs associés aux différents objets (!) ; (si mes souvenirs de mathématiques sont corrects, les normes des vecteurs sont vraiment et simplement différentes),

mon raisonnement m'apparaît tellement simple (voir simpliste), que je crois possiblement me perdre,
peut-être voyez-vous l'erreur ou une erreur, parce que de mon côté, je ne la vois pas,
dîtes-moi,

merci,

s'il n'y a pas erreurs (?), et si nécessaire, je peux étayer en revenant aux remarques, que vous avez pu exprimer dans cette discussion et une autre fermée depuis : Noyaux des atomes et gravité locale,

[Sethy]

Nous avons déjà eu cette discussion.

Je reprends la même idée qui montre bien l'idée d'attraction "universelle".



Note u.a. = unité arbitraire de force.

[gts2]

pourtant cela ne me semble pas similaire,
- si on considère la valeur des "forces", sans doutes oui,
- mais pas du tout, en terme de vecteurs associés aux différents objets (!) ; (si mes souvenirs de mathématiques sont corrects, les normes des vecteurs sont vraiment et simplement différentes),

De quels vecteurs parlez-vous ? Si ce sont les forces elles sont égales en terme de vecteur (intensité/norme, direction, sens, valeur ...).
Par contre, les effets seront différents : deux forces identiques appliquées à deux objets différents ne donnent pas le même mouvement, ce sont ces vecteurs dont vous voulez parler ?

[franklin.]

Bonjour,

De quels vecteurs parlez-vous ? Si ce sont les forces elles sont égales en terme de vecteur (intensité/norme, direction, sens, valeur ...).
Par contre, les effets seront différents : deux forces identiques appliquées à deux objets différents ne donnent pas le même mouvement, ce sont ces vecteurs dont vous voulez parler ?

... merci, oui effectivement, après avoir posté le message, j'ai remarqué, que je n'ai pas précisé à quelle grandeur ces vecteurs étaient associés ?
Dans l'idée exprimée, (ce à quoi je pensais), ce sont les vecteurs, qui sont associés à l'accélération des différents objets,
corrigez si cela vous semble erroné,

merci

[franklin.]

...en précisant aussi que l'accélération de A' et B' est la même, bien sûr

[gts2]

C'est bien cela, les objets de masses différentes sont soumis à la même force et accélèrent différemment.
Mais cela est très général.

[franklin.]

Bonsoir,

maintenant, j'envisage d'autres valeurs arbitraires :

par exemple, je pose, que A et A' ont même masse, disons 4 kg,
et je pose, que la masse de B est 1 kg et la masse de B' 2 kg.

La lune ne fait bien sûr pas 4 kg, mais d'une certaine manière, en posant A et A' de masses égales, on se retrouve un peu dans la situation de comparer la chute du marteau et de la plume, par rapport à un seul et même objet, la lune de masse inchangée. (En effet, comme la lune, ici, la masse de A et celle de A' étant les mêmes, on peut considérer A et A', comme un seul et même objet, disons donc A) ;
si on considère alors, que B' est le marteau et B, la plume, en tout cas, si on considère deux objets de masses différentes, relativement à cet unique objet A,
on obtient, que FA/B = 4G/d² est différente de FA/B' = 8G/d²,
et cela engage alors mon questionnement, en ce qui concerne le principe d'équivalence faible.
Effectivement, dans cet exemple, il semble que ce principe n'est pas respecté dans les conditions où Mb et Mb' ne sont pas négligeables par rapport à Ma.

Est-ce que je fais erreur ?

Merci.

[gts2]

Principe d'équivalence faible... il semble que ce principe n'est pas respecté dans les conditions où Mb et Mb' ne sont pas négligeables par rapport à Ma.

Je ne vois pas pourquoi il n'est pas respecté, pourriez-vous précisez ?

[Deedee81]

Salut,

on obtient, que FA/B = 4G/d² est différente de FA/B' = 8G/d²,
et cela engage alors mon questionnement, en ce qui concerne le principe d'équivalence faible.
Est-ce que je fais erreur ?

Oui

Le principe d'équivalence (faible ou fort d'ailleurs) ne concerne pas la comparaison entre la force de deux objets et la force de deux autres objets. Si elle était identique ce serait d'ailleurs franchement bizarre. Pourquoi la force entre A et B et la force entre A ety B' devraient-elles être égales ? Pourquoi la force entre la Terre et le Soleil et la force entre la Terre et la Lune devraient-elles être égales. Le principe d'équivalence concerne UN et UN SEUL objet plongé dans un champ gravitationnel (dû à quelque chose mais peu importe).

Plus précisément :
- Le principe d'équivalence faible dit que la masse gravitationnelle (celle qui intervient dans F = Gmm'/d²) et la masse inertielle (celle qui intervient dans F = ma) sont proportionnelles (avec toujours la même constante de proportionnalité qu'on a évidemment choisi égale à un, même unités donc) quelle que soit la composition. Il faut que le corps en question soit petit et de faible masse (petit car la gravité peut varier entre deux points, et de faible masse pour qu'il n'affecte pas le corps à l'origine du champ gravitationnel. Ce n'est pas le cas de la Lune dont l'attraction sur la Terre n'est pas négligeable. Le passage à des corps plus gros ou plus massif se fait donc par des techniques parfois sophistiquées du genre calcul intégral : ça revient à découper (mentalement) le gros corps en pleins de petits corps et à faire la somme).
- Le principe d'équivalence fort : idem sauf qu'on dit qu'il n'y a qu'UNE seule masse (masse gravitationnelle = masse inerte non pas au sens "même valeur" mais au sens "même identité")
- Le principe d'équivalence en relativité générale, il peut se traduire simplement en disant qu'en tout point de l'espace-temps, il existe un système (local !) de coordonnées tel que la relativité restreinte est valide dans un voisiage infinitésimal de ce point. Sa revient à dire que l'espace-temps plat tangent à l'espace-temps en ce point (même notion que la droite tangente à une courbe mais généralisé à 4D) est l'espace-temps de Minkowski. C'est une des clefs de la formulation mathématique de la RG.