Fonction de transfert système avec perturbations

[JulesMhz]

Bonjour,

Je suis sur un exercice sur lequel je butte, dont voici l'énoncé :

On veut maintenir à la verticale une fusée pendant la phase atmosphérique de sa trajectoire.
Pour ce faire, on fait pivoter la tuyère du moteur principal suivant deux axes. En première approximation, les dynamiques de chacun des deux axes sont à peu près découplées, et l’on peut donc les modéliser séparément. On s’intéresse ici à l’un de ces deux axes d’évolution. La variable de sortie est l’angle d’inclinaison du lanceur et la variable de commande l’angle de braquage de la tuyère dans ce plan. Le temps (mesuré en secondes) est noté . Quand et restent tous les deux proches de , un modèle simplifié du comportement du système est donné par l’équation différentielle :

d²y(t)/dt²-4y(t) = 2u(t) + v(t)

Où v(t) est une perturbation principalement liée au vent.

Question 1, on me demande de calculer la transformée de Laplace de y en fonction des transformées de Laplace de u et de v et des conditions initiales du système (y(0)et y'(0)), à ce stade je ne pense pas me tromper en écrivant :
Y(p)= (2/(p²-4))*U(p) + (1/(p²-4))*V(p) + (1/(p²-4))*(p*y(0)+y'(0))

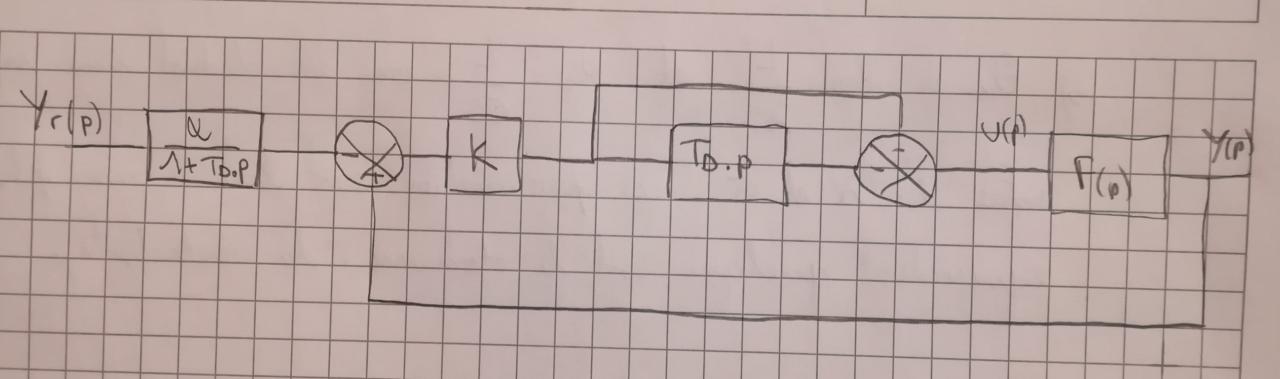
Question 2, on me demande la fonction de transfert F(p) du système à asservir (c'est-à-dire du système d'entrée u et de sortie y). Ce système est-il stable (justifiez votre réponse) ? Dessiner un schéma-bloc du système à asservir avec perturbation.

La j'ai un doute, car si je divise mon résultat de la question 1 par U(p) pour avoir F(p)=Y(p)/U(p), j'obtiens :
F(p) = (2/(p²-4)) + (1/(p²-4))*V(p)/U(p) + (1/(p²-4))*(p*y(0)+y'(0))/U(p)

Ce qui ne me plait pas trop, ce n'est pas de la forme des fonctions de transfert "habituelles", quelle est la bonne méthodologie ?

En ce qui concerne la stabilité, ma réponse pour le moment est que le système est instable car le coefficient d'amortissement (dans p²-4) est nul, mais le fait d'avoir une valeur négative (-4) me chagrine et me fait penser que ce n'est pas correct...

Merci pour vos éclaircissements...
-----

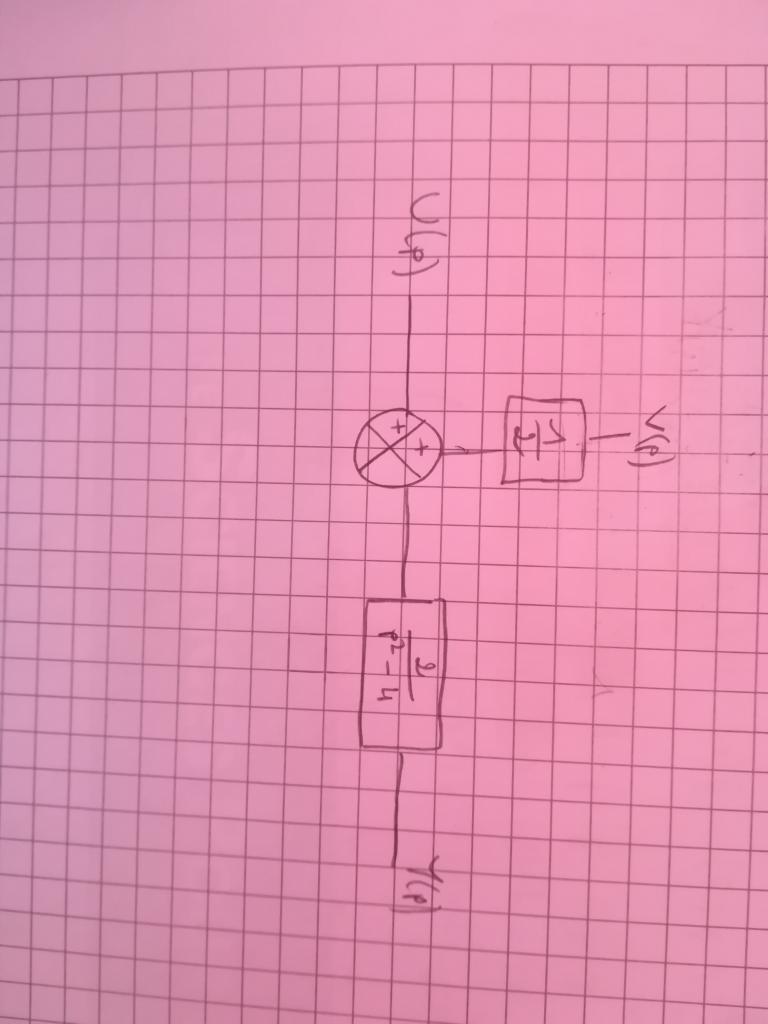
[gts2]

La fonction de transfert est classiquement F(p)=2/(p²-4).
Le problème des perturbations se résout en ajoutant à l'entrée de F(p) un additionneur entre u et v.
Chercher "schéma bloc perturbation"

On voit directement sur l'équation différentielle y''-4y=... que cela est en effet instable.
Plutôt que la valeur nulle de y' (qui est une approximation), c'est surtout le signe de -4y qui crée l'instabilité. Sur l'équa diff. solution en exp(+2t) qui diverge.
Sur le dénominateur, la règle est : "stable si tous les coefficients sont de même signe".

[JulesMhz]

Bonjour,
Merci pour votre réponse c'est très clair.

Du coup j'obtiens pour schéma bloc :


Ensuite on me demande les réponses impulsionnelle et indicielle, je trouve respectivement sinh(2t) et cosh(2t). Est-ce bien cela ?

Merci encore.

[gts2]

Pour la réponse impulsionnelle, OK avec simplement une remarque : cela correspond à y(0)=0 et y'(0)=0

Pour la réponse indicielle, par contre, vous n'auriez pas mis p de l'échelon au numérateur plutôt qu'au dénominateur ?

[A voir en vidéo sur Futura]

[JulesMhz]

J'ai bien mis le p de l'échelon au dénominateur, voici le raisonnement j'ai appliqué :

S(p) = (1/p) * (2/p²-4), donc p.S(p) = 2/p²-4, donc j'en déduis que la dérivée de S(p) vaut 2/p²-4, donc ma sortie c'est la primitive de sinh(2t) soir cosh(2t).

Mais à priori mon raisonnement doit être faux

[gts2]

Deux problèmes :

1- primitive de sinh(2t) = cosh(2t), il manque le 1/2 d'intégration
2- une primitive est définie à une constante près et elle manque.

Pourquoi ne prenez-vous pas Laplace inverse de ?

[JulesMhz]

Pourquoi ne prenez-vous pas Laplace inverse de ?

Bonne question... Du coup je trouve sinh²t.

Merci pour votre aide !

[gts2]

Bien, d'autant que sinh²t=1/2 cosh(2t)-1/2

On retrouve bien votre cosh(2t) et le terme constant en plus.

[JulesMhz]

Bonjour,

Bon j'abuse un peu mais je suis bloqué un peu plus loin dans l'exercice, pour la suite l'énoncé nous dit :

On utilise pour commander le système (1) un régulateur proportionnel-dérivé de la forme
u (t) = -k ( y(t) - alpha.yr (t) + Td.dy(t)/dt )
Où k > 0, Td > 0 et alpha > 0 sont trois constantes, et où yr (t) est une consigne d'inclinaison.
L'objectif de commande est alors d'annuler l'erreur de poursuite :
eP (t) = y (t) - yr (t)
1/ Déterminer la fonction de transfert C (p) du régulateur proportionnel-dérivé et la fonction
de transfert de la chaîne directe T (p) (fonction de transfert de boucle) de cet asservissement.
Montrer qu'en prenant r (t) = (alpha.yr (t))/(1+Td.p), le système asservi peut se mettre sous la forme standard
du Chapitre 6 du polycopié de cours, et dessiner un schéma-bloc du système asservi.


Tout d'abord, j'ai mis en pièce jointe le schéma-bloc que je trouve, il me parait plutôt pas mal puisque je retrouve bien la forme du régulateur donnée. Pour la fonction de transfert du régulateur je trouve simplement C(p)=-K(1+Td.p), ce qui me parait coéherent. J'ai un doute quant à la fonction de transfert de la chaine directe T(p), je sais que T(p)=C(p)*F(p), donc j'en déduit -K*(1+Td.p)*(2/p²-4), mais ce qui me chagrine c'est, que fait-on des perturbations ? Pourquoi on ne le fait pas apparaitre ? Ou alors où est-ce que je me trompe ?

Merci encore...

[gts2]

Je ne suis pas automaticien... Donc mes remarques sont à prendre avec des pincettes.
OK pour le bloc d'entrée. Par contre le soustracteur je l'aurai intervertit + pour ce qui vient de la commande (c'est quand même le but) et - pour l'entrée Y.
Ce qui permet d'avoir un correcteur avec un + plus raisonnable.
Ensuite le dessin de votre C est bizarre (pour moi ...), pourquoi ne pas mettre tout simplement un bloc K(1+Tp *p) ?
C'est une habitude de dessiner 1+a comme cela avec un noeud et un additionneur ?

Si vous voulez mettre les perturbations, il faut mettre un additionneur à l'entrée de F(p) avec à une entrée U et à l'autre la perturbation V/2.

soit T(p)= + K*(1+Td.p)*2/(p²-4) (avec la parenthèse au bon endroit et un signe + )

Mais voir la première phrase...

[stefjm]

La fonction de transfert est classiquement F(p)=2/(p²-4).
Sur le dénominateur, la règle est : "stable si tous les coefficients sont de même signe".

Pour des systèmes de degré inférieur ou égal à 2.
Au delà, la condition n'est que nécessaire, pas suffisante.

Contre-exemple : p^3+p^2+p+1=(p + 1) (p^2 + 1) : 3 fois instables
-1 est négatif
i et -i ont une partie réelle non strictement négative.

Cordialement.

[stefjm]

Je ne suis pas automaticien...

Un peu quand même.

Ensuite le dessin de votre C est bizarre (pour moi ...), pourquoi ne pas mettre tout simplement un bloc K(1+Tp *p) ?
C'est une habitude de dessiner 1+a comme cela avec un noeud et un additionneur ?

C'est très utilisé pour la représentation d'état, en général avec des intégrateurs.
Je l'ai rarement vu sous cette forme pour le correcteur.