Efforts sur les pieds d'une table

[Mate97]

Bonjour à tous,
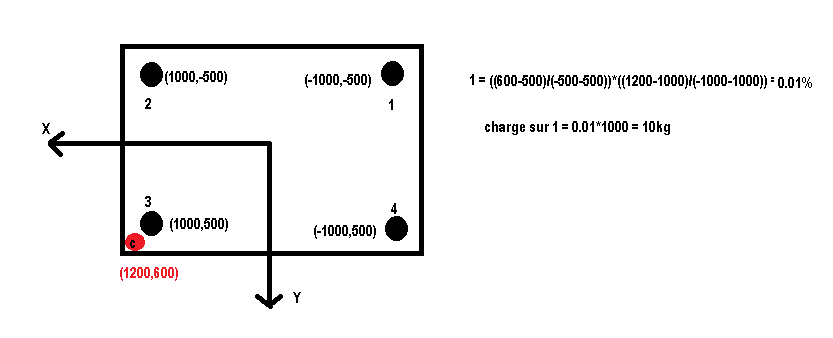
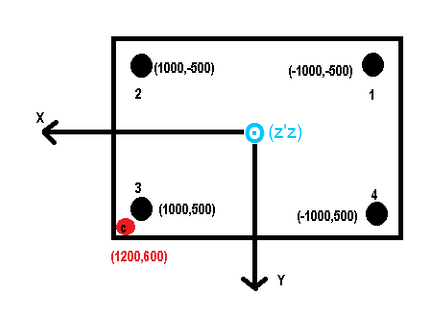
Il y a un point que je n'arrive pas à comprendre dans ce problème. Je chercher à trouver la répartition de la charge C1 (1000 kg) sur les 4 pieds de la table.
Avec la formule ci-dessus je trouve un effort important suivant le pied 3 qui est logique, des efforts négatifs pour les pieds 2 et 4. Le problème est que je trouve un effort positif pour le pied 1, je n'arrive à concevoir un tel résultat, étant donné que je trouve les mêmes valeurs en appliquant le PFS. Quelqu'un pourrait m'éclairer?

Cordialement
-----

[harmoniciste]

Bonjour, Si on suppose une table infiniment rigide, seuls trois pieds sont en contact avec le sol. Le quatrième pied ne transmet donc aucun effort. Si votre table ne pèse rien, aucun équilibre n'est possible.

[Dynamix]

Salut

La charge est en dehors du "polygone de sustentation" , donc en déséquilibre .
Seul le pied 3 équilibre le poids , mais pas le moment .
Les autres pieds ne servent strictement à rien .

IRL , il faudrait tenir compte du poids de la tables .

[Mate97]

D'accord mais prenons une table de masse 10 kg avec son centre de gravité aux coordonnées (0;0), le problème est toujours présent, comment modifier les calculs lorsque la charge est placée en dehors du polygone de sustentation ?

[A voir en vidéo sur Futura]

[Resartus]

Bonjour,
Une table a 4 pieds est hyperstatique, c'est à dire qu'on ne peut pas connaitre toutes les réactions seulement avec la position du centre de gravité.
Même si on peut supposer par symétrie que la table non chargée avait des réactions égales, cela ne suffit pas pour traiter l'ajout de la charge excentrée (et le fait que la charge soit dans ou hors du polygone ne change rien à ce constat)
Pour vous en convaincre, écrivez toutes les équations disponibles pour les forces et leurs moments : il y en 3, pour 4 inconnues…
Pour résoudre, il faudrait faire des hypothèses complémentaires, par exemple supposer que l'élasticité des pieds est identique (mais d'autre hypothèses sont envisageables) et prendre en compte les déformations de ces pieds
Il y a en RDM diverses méthodes (méthode des forces, méthode des déplacements, etc.) pour traiter ces problèmes hyperstatiques. Mais c'est sans doute au delà de ce qui vous est demandé. Pourrait-on avoir le texte exact de la question?

[Dynamix]

D'accord mais prenons une table de masse 10 kg avec son centre de gravité aux coordonnées (0;0), le problème est toujours présent

Effectivement c' est insuffisant pour que le système soit en équilibre .
Voir les moments par rapport au pied 3 .

, comment modifier les calculs lorsque la charge est placée en dehors du polygone de sustentation ?

Le PFS ne s' applique plus , il faut utiliser le PFD pour déterminer le basculement de la table autour du pied 3

[Mate97]

J'ai beau chercher je ne vois pas comment appliquer la méthode des forces dans ce cas

[Dynamix]

la méthode des forces

Quelle est cette "méthode des forces" ?

[Opabinia]

Bonjour,

Tu est en présence d'un système indéterminé, puisque le nombre d'inconnues (les 4 composantes F₁, F₂, F₃, F₄ des forces verticales) dépasse le nombre d'équations (3) traduisant l'équilibre statique.
Et un peu de réflexion amène à penser que l'un des pieds au moins (n° 1) doit être fixé au sol afin de prévenir tout basculement: il y a donc une composante négative.

Pour la relation manquante, il suffit d'imaginer un basculement infime (selon une orientation indéterminée) du plateau de la table, supposé rigide, et les réactions des pieds proportionnelles au déformations produites: les composantes cherchées sont alors fonctions bilinéaires des coordonnées (x, y), ce qui entraîne compte tenu de la symétrie rectangulaire:

F₁ + F₃ = F₂ + F₄ .

[Black Jack 2]

Bonjour,

Le centre de la table, le pied 3 et le point C d'application de la force (verticale vers le bas je présume) sont alignés.

Si la table est posée sur le sol (pieds non attachés au sol), il y aura basculement autour du pied 3 si : (Force en C) > 5 * (Poids de la table)

Donc si la force en C est de (1000*g) (SI) , il y aura basculement autour du pied 3 si la table a une masse de moins de 200 kg.

[Dynamix]

F1+ F3 = F2 + F4

Non !
Totalement faux .
F3 = 1000g
F1 = F2 = F4 = 0