Bonjour à tous,
dans mon cours de mécanique des fluides, on aborde les fluides turbulents. Il y est dit que ces fluides sont non-newtoniens et qu'ainsi ils ne peuvent être modélisés par les équations de N-S qui correspondent aux équations de la dynamique des fluides newtoniens.
Or plus tard dans le cours, il est noté que le mouvement de turbulence peut être résolu théoriquement (évidemment je sais que l'existence, stabilité et unicité des solutions de N-S n'est pas prouvée pour chaque configuration fluide) en prenant les équations de N-S et en réalisant des simulations avec un pas de temps très discret et des grandes échelles de fluctuations turbulentes.
Je suis donc un peu confus. D'une part il nous a été présenté que 90% des fluides utilisés dans l'industrie obéissaient à un comportement newtonien (dont l'eau et l'air ambiant) mais sur d'autres sources je trouve que l'air et l'eau ne sont pas des fluides newtoniens (et il est vrai que l'air crée des turbulences...). Quelle information est correcte ? De plus, je sais qu'une des méthodes pour modéliser les turbulences est l'approche statistique des équations moyennées de N-S (de Reynolds), quid donc de la résolution du mouvement de turbulences par les équations simples 3D instationnaires de N-S ?
Merci d'avance pour vos réponses, et bonne fin d'année !
-----




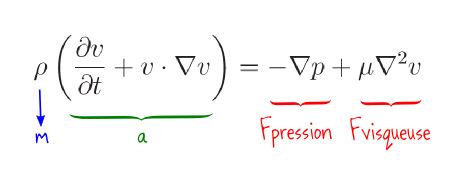 : c'est : pourquoi la pression est-elle en négatif, puisqu'il est évident qu'elle l'emporte à tous les coups dans l'écoulement d'un débit quel qu'il soit et pourquoi on ne s'intéresse pas au rapport entre l'accélération due à la pression / l'accélération due au freinage visqueux. Bien entendu, on obtient un rapport d'efficacité du mouvement, sans dimension.
: c'est : pourquoi la pression est-elle en négatif, puisqu'il est évident qu'elle l'emporte à tous les coups dans l'écoulement d'un débit quel qu'il soit et pourquoi on ne s'intéresse pas au rapport entre l'accélération due à la pression / l'accélération due au freinage visqueux. Bien entendu, on obtient un rapport d'efficacité du mouvement, sans dimension.