Bonjour, je me pose une question autour de la capacité des condensateurs.
On peut trouver que des farads correspondent à des secondes par ohm avec des formules:
C=q/U
C=(U*t/R)/U
C=t/R
Mais ça n'explique rien de concret : à quoi correspondent ce temps et cette résistance ?
Si quelqu'un est capable de l'expliquer pour le cas d'un condensateur, je veux bien. Merci d'avance
-----




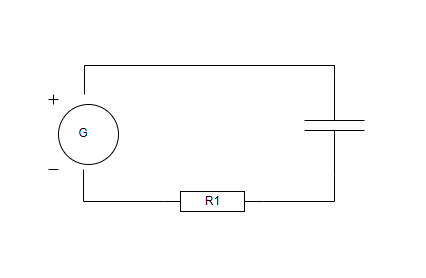

 qui permet de passer d'un courant à une variation de tension par unité de temps.
qui permet de passer d'un courant à une variation de tension par unité de temps.