Salut, je suis en train d'étudier l'équilibre et la dynamique des corps en rotation et je suis tombée sur un exercice que je ne sais pas faire. Il est sensé être facile mais je ne sais pas du tout comment l'envisager:
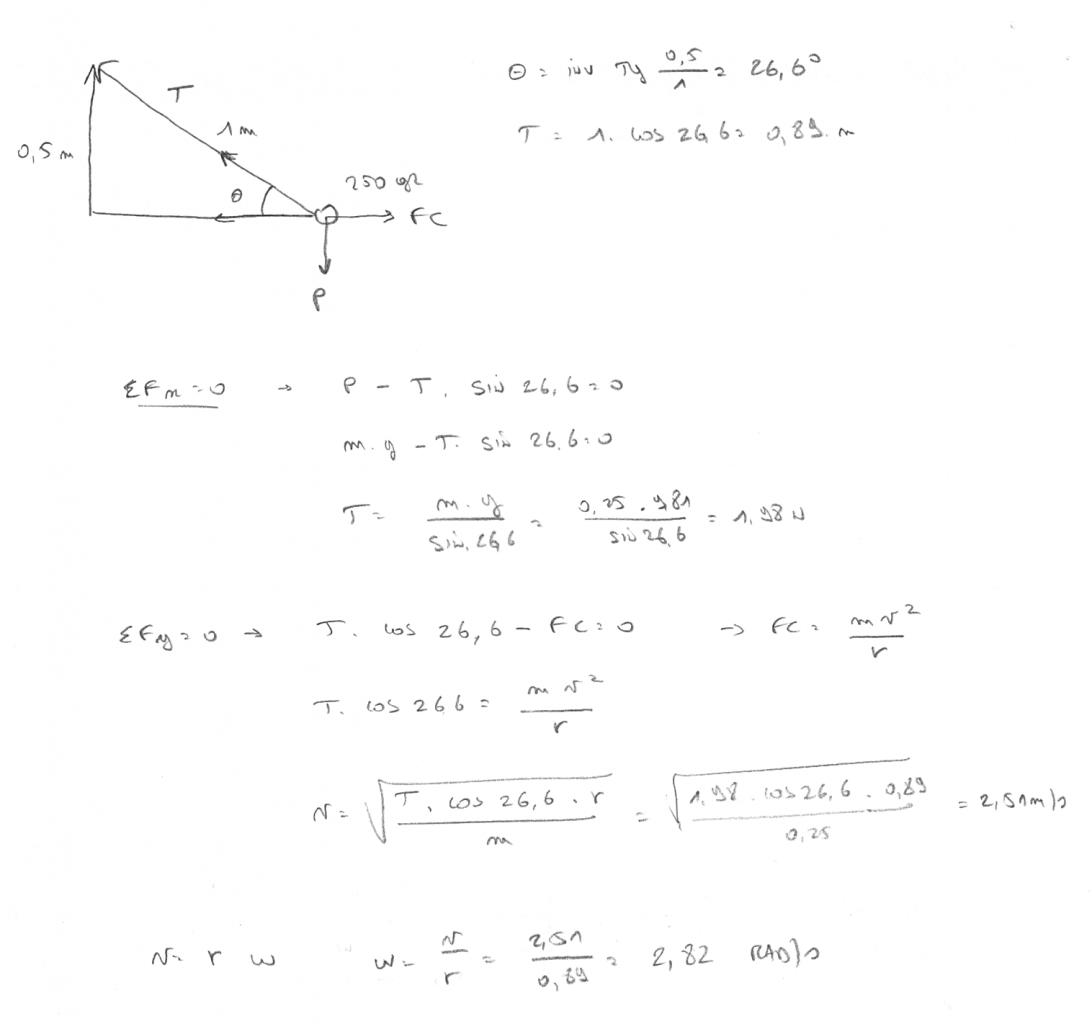
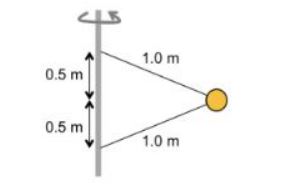
"Une balle de 250 gr fait un tour dans le plan horizontal. Quelle est la vitesse angulaire minimale de la balle pour que les cordes soient tendues?"
Merci beaucoup pour votre aide
Bonjour,
On peut tirer sur une corde, mais pas la pousser, autrement dit si la corde est tendue, cela impose le sens de la tension.
Il suffit donc de calculer celle-ci et d'imposer son sens pour trouver la relation.
Bonjour ,
Est ce une erreur de ma part : on peut remplacer les 2 cordes actuelles par la corde virtuelle horizontale qui serait la hauteur du triangle ?
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Bonjour,
La corde virtuelle sera inclinée (il faut bien compenser le poids), donc cela revient à remplacer deux inconnues (T1,T2) par deux inconnues (T, angle).
Bonjour,
Vous connaissez la relation entre la vitesse angulaire et l'accélération centripète ?Envoyé par martix
Bonjour Tifoc,
Oui je connais la relation entre la vitesse angulaire et l'accélération centripète (ac): ac = v^2/r = rω^2
J'arrive à calculer le rayon (quand les cordes sont tendues); 1^2 = 0,5^2 + r^2 ... r= 0,87
Mais je ne sais pas comment chercher v ou ω;
v serait déplacement / intervalle de temps. Je pourrais calculer le déplacement par 2 π r, mais je me retrouve en qu'on connait pas l'intervalle de temps.
Et je sais calculer ω comme ω = v/r (Mais vu que je ne sais pas comment calculer v je ne peut pas appliquer cette formule)
La somme des tensions des cordes vous donne une force dont la direction est orientée dans l'angle au sommet du triangle.
Le cas limite est celui pour lequel, la somme des accélérations serait suivant la corde du haut, la tension sur celle du bas s'annulerait.
Cela vous donne une vitesse de rotation minimale.
Comprendre c'est être capable de faire.
Bonjour,
Oui, c'est une erreur.
Si tu as une seule corde horizontale ... il faudra une vitesse de rotation infinie.
Dans le cas de l'exercice, pour trouver la vitesse de rotation minimale ... il n'y aurait aucune force dans la corde du bas. (comprendre évidemment pourquoi)
Cela rend alors l'exercice aisé.
Oui , merci , c'est bien tout ce qui me paraissait une erreur ...
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
C'est un problème de mécanique, si vous n'écrivez pas, au minimum, le principe fondamental, vous ne pouvez avancer.
Vous connaissez l'accélération, avec les indications que l'on vous donne, cela devrait suffire.
B'jour,
Comme le dit implicitement gts2 dans le message précédent, il faut d'abord trouver les forces en jeu. C'est un bête problème de statique.
Indice : trouver la force minimum, ce qui implique que la corde du bas est tendue mais sans contrainte.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
Bonjour,
Je me retrouve confronté à la même question, et une fois de plus, je ne vois pas comment aborder la question.
"C'est un problème de mécanique, si vous n'écrivez pas, au minimum, le principe fondamental, vous ne pouvez avancer."
Est-ce correct de dire que : T = FCentripède donc T=m.g.sin x (x étant l'angle entre la corde et l'horizontale) ?
En même temps, ça ne me donne pas la direction à suivre pour trouver la vitesse angulaire.
Merci.
Bonjour,
D'où sort le "donc" dans T=FCentripède le poids n'intervient pas alors qu'il apparait dans la conclusion m.g.sin x
Le principe fondamental ditet pas T=FCentripède
Bonjour,
Pouvez-vous me dire si ma résolution est correcte? Merci.
Bonjour,
Il y a déjà une erreur à la première ligne : Theta = arcsin(0,5/1) = 30° et pas ce que tu as écrit.
Bonjour,
Autre remarque : faites les calculs en littéral : vous vous apercevriez que la valeur de la masse m n'intervient pas et qu'il est inutile de calculer T (et si la question est de calculer w, il n'est pas nécessaire de calculer v)
A partir des deux projections vous avez immédiatement sin(alpha)=...
Dernière modification par gts2 ; 21/07/2023 à 13h25.
Effectivement, concernant le sinus, j'ai vraiment manqué de flair!
Dernière modification par Vctpil ; 21/07/2023 à 16h24.
"Autre remarque : faites les calculs en littéral : vous vous apercevriez que la valeur de la masse m n'intervient pas et qu'il est inutile de calculer T (et si la question est de calculer w, il n'est pas nécessaire de calculer v)
A partir des deux projections vous avez immédiatement sin(alpha)=..."
Je n'ai pas compris, je ne vois vraiment pas comment vous arrivez à résoudre le problème sans m et v. Pourriez-vous me donner un exemple?
Merci.
Je reprend simplement vos calculs :
m apparait deux fois, si vous faites le rapport m disparait (et T également qu'il n'est donc pas nécessaire de calculer).
Dernière modification par gts2 ; 21/07/2023 à 17h02.
Merci, je vais essayer de voir comment résoudre le problème de cette manière.
