Champ magnétique généré par un dipôle magnétique en coordonnées cartésiennes

[Metwurchr]

Bonjour,
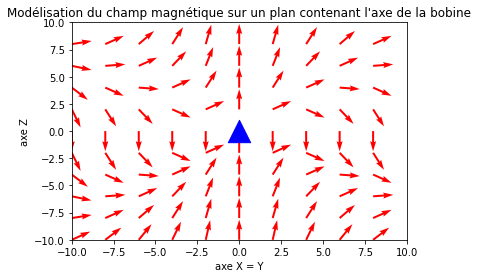
Je tente de simuler un champ magnétique généré par une boucle de courant sur python.
image_2021-06-06_161245.png
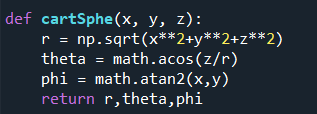
J'ai ces équations dans la base sphérique que je veux passer dans la base cartésienne (O,ex,ey,ez)

J'ai donc transformé mes paramètre r, phi et theta en fonction de x,y et z :
image_2021-06-06_161701.png

Et ensuite j'ai écrit mes vecteurs de la base sphérique en fonction de ex, ey et ez
image_2021-06-06_161844.png

Pour finalement obtenir mes composantes Bx, By et Bz en fonction de r, theta et phi (puis dans le programme en fonction de x,y et z)

image_2021-06-06_162035.png

J'imagine que je ne suis pas le premier à faire ça et j'aimerais savoir si mon raisonnement est bon.
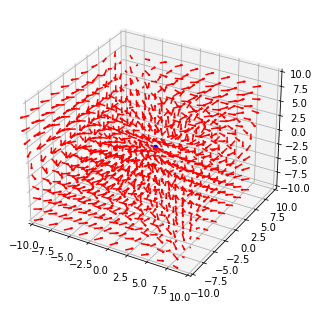
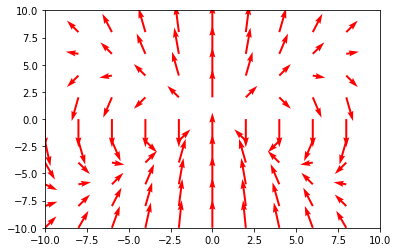
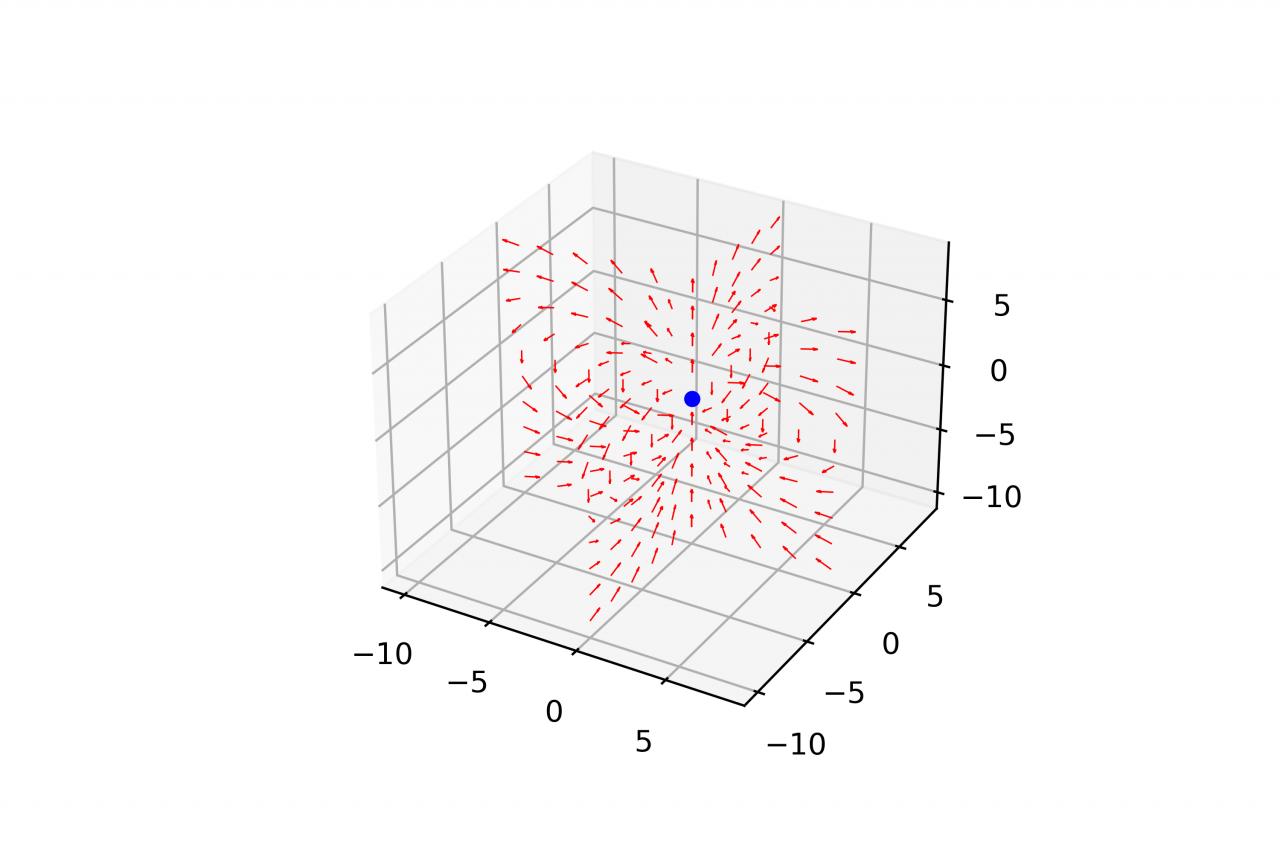
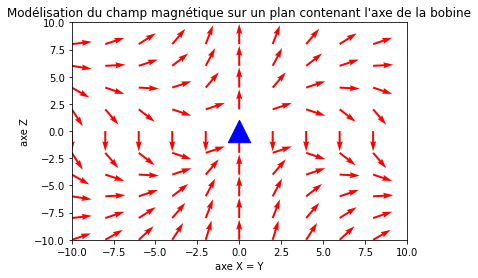
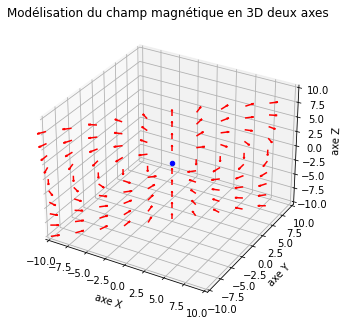
Je pense qu'il y a une erreur parce que le champ magnétique en 3d ne ressemble pas au champ magnétique auquel on pourrait s'attendre.

image_2021-06-06_162246.png
-----

[gts2]

Bonjour,

Qu'utilisez-vous en Python pour calculer ?

Autrement dit si tan(\phi)=y/x alors \phi=atan2(y,x), atan2 renvoyant entre -pi et +pi, contrairement à tan-1 qui est à image dans -pi/2 +pi/2..

[Metwurchr]

Alors j'utilise np.arctan(y/x) qui renvoie effectivement dans -pi/2, pi/2
Par contre je ne suis pas sûr de comprendre cette histoire de atan2(y,x)

[obi76]

atan2(y,x) vous donne le "vrai" angle entre -pi et pi, en prenant en compte le signe de y. En fait le ratio y/x ne vous permet pas de savoir si vous êtes entre -pi/2 et pi/2 ou entre pi/2 et 3pi/2. Pour ça il faut prendre en compte le signe de y, ce que atan ne fait pas, mais ce que atan2 fait (c'est d'ailleurs pour ça que les arguments y et x dans atan2 sont séparés, et pas dans atan où seul le ratio y/x est l'argument d'entrée, ce qui ne permet pas à la fonction de savoir si y est positif ou négatif).

C'est un piège assez courant quand on code de la trigo.

[A voir en vidéo sur Futura]

[Metwurchr]

Alors j'ai du modifier quelques trucs dans mon programme, notamment le fait que math.atan ne gère pas les array contrairement à np.arctan mais bref j'ai reussi.
Ca inverse effectivement la moitié de mon plot3D.

Honnêtement ça me semble pas mal (mieux qu'avant). Je ne sais pas trop si c'est juste n'hésitez pas à donner votre avis
Au fait je l'ai pas précisé dans le premier message mais les vecteurs sont normalisés pour qu'on y voit quelque chose.

[gts2]

Bonjour,

Vu que le problème est de symétrie de révolution autour l'axe porté par le moment magnétique, faites deux ou trois coupes dans un plan contenant cet axe, cela sera plus lisible pour vérifier la cohérence.

[Metwurchr]

Alors ça c'est une idée super intelligente !

ça m'a tout l'air d'être cohérent en tout cas
Merci beaucoup pour votre aide

[obi76]

En tous cas la coupe parait nickelle. Si c'est pareil dans tous les plans possédant cet axe, c'est tout bon (regardez dans le plan perpendiculaire)

[Metwurchr]

Alors j'avoue que je suis un peu déçu par le plan donné par la droite d'équation X=Y et Z

[obi76]

Donc il reste un problème...

Cette histoire de atan2, je pense, permettrait d'améliorer les choses, testez-le...

[Metwurchr]

C'est déjà fait ça, et effectivement ça a amélioré les choses.
D'ailleurs voici ma fonction qui transforme mes coordonnées sphériques en cartésiennes :


Je vais essayer de jouer sur d'autres paramètres mais là je sèche un peu

[obi76]

Là ce soir je n'ai pas la motivation, mais si vous mettiez tout le code, je regarderai peut-être ça demain, sinon d'autres pourront regarder d'ici là...

[Metwurchr]

J'ai créer un google collab pour vous partager le code
Je vais continuer à chercher également de mon côté
https://colab.research.google.com/dr...r9?usp=sharing
merci pour l'aide

[obi76]

si vous aviez autre chose que gogole (qui est blacklisté chez moi, et pour cause...) ce serait parfait

Ce ne sont pas les alternatives libres qui manquent

[Metwurchr]

Bon ce sera pas très beau sans les couleurs mais voila le code

import numpy as npimport matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
import math


mu0 = 4*np.pi*10**-7
S = 0.45 #surface d'une spire
n = 125 #nombre de spires
t= 5#on définit le temps à 5 secondes dans cette simulation pour avoir un courant maximum


def I(t): #Courant dans la bobine. Une impulsion de 0.2s à 457kHZ toutes les secondes
    t = t%1
    if t <=0.2:
        return 3*np.cos(2*np.pi*457*10**3*t)
    else :
        return 0
    
def cartSphe(x, y, z): #transformation des coordonnées cartésiennes en sphérique
    r = np.sqrt(x**2+y**2+z**2)
    theta = math.acos(z/r)
    phi = math.atan2(y,x)
    return r,theta,phi


def spheCart(r, theta, phi, Br, Btheta): #transformation des coordonnées sphériques en cartésiennes
    Bx = Br*np.sin(theta)*np.sin(phi)+Btheta*np.cos(theta)*np.cos(phi)
    By = Br*np.sin(theta)*np.cos(phi)+Btheta*np.cos(theta)*np.sin(phi)
    Bz = Br*np.cos(theta)-Btheta*np.sin(theta)
    return Bx,By,Bz
    
M = lambda t: n*S*I(t) #Moment magnétique
    


def champ(x, y, z): #définition du champ magnétique dans les coordonnées sphériques
    r,theta,phi = cartSphe(x, y, z)
    Br = (mu0*M(t)*np.cos(theta))/(2*np.pi*r**3)
    Btheta = (mu0*M(t)*np.sin(theta))/(4*np.pi*r**3)
    Bphi = 0
    return spheCart(r, theta, phi, Br, Btheta)


"""
Affichage des résultats
"""




fig = plt.figure()
ax = Axes3D(fig)




LX, LY, LZ = 10,10,10  #paramètres de maillage xyz
gridwidth=2 # où on calcule les points
X, Y, Z= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth),np.arange(-LZ, LZ, gridwidth) ) #Génération de maillage


R = np.sqrt(X**2+Y**2+Z**2)
#Coordonnées de position et charge de la charge ponctuelle
X1,Y1, Z1=0,0,0
Q1=1
R1=np.sqrt((X-X1)**2+(Y-Y1)**2+(Z-Z1)**2)
ax.scatter3D(X1,Y1,Z1,"^", color='blue')




U = np.zeros((LX,LY,LZ));V = np.zeros((LX,LY,LZ));W = np.zeros((LX,LY,LZ)) #Remplissage des vecteurs
for L in range(len(X)):
    for l in range(len(X[L])):
        for h in range(len(X[L][l])):
            U[L,l,h],V[L,l,h],W[L,l,h] = champ(X[L,l,h],Y[L,l,h],Z[L,l,h])
            






ax.quiver(X, Y, Z, U, V, W, color='red',length=1, normalize=True)


ax.set_xlim([-LX, LX])
ax.set_ylim([-LY, LY])
ax.set_zlim([-LZ, LZ])
plt.title('Modélisation du champ magnétique en 3D')
ax.set_xlabel('axe X')
ax.set_ylabel('axe Y')
ax.set_zlabel('axe Z')
plt.savefig('champ magnétique.png', dpi = 500)
plt.show()

[gts2]

Avec

Bx = Br*np.sin(theta)*np.cos(phi)+B theta*np.cos(theta)*np.cos(phi )
By = Br*np.sin(theta)*np.sin(phi)+B theta*np.cos(theta)*np.sin(phi )

Cela donne :

[Metwurchr]

Vous avez parfaitement raison, c'est ce que je dois faire.
Mais par contre cela ne change rien sur le plan diagonal

[Metwurchr]

ah quoique
Ca a l'air pas mal comme ça en fait

[Metwurchr]

Je viens de tout retester, ça marche parfaitement, c'était effectivement le problème de l'atan2 et une erreur de calcul qui m'a fait inversé un cos et un sin.
Merci à tout les deux pour votre aide

[gts2]

Bonne continuation.