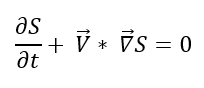Bonjour,
Dans mon cours de mécanique des fluides, lorsqu'on parle des conditions aux limites des fluides parfaits on avait à cette expression : DS/Dt = 0 où S est l'équation de la paroi et D/Dt est la dérivée particulaire.
Je n'arrive pas à saisir le sens physique de cette expression car en suivant la formule de la dérivée particulaire, on peut dire que :
Y a-t-il une interprétation physique à retirer de cette expression ?
Merci d'avance.
-----



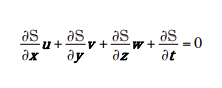
 ? Puis que représente
? Puis que représente