Bonjour à tous je voudrais avoir de l'aide pour cet exercice qui me pose problème
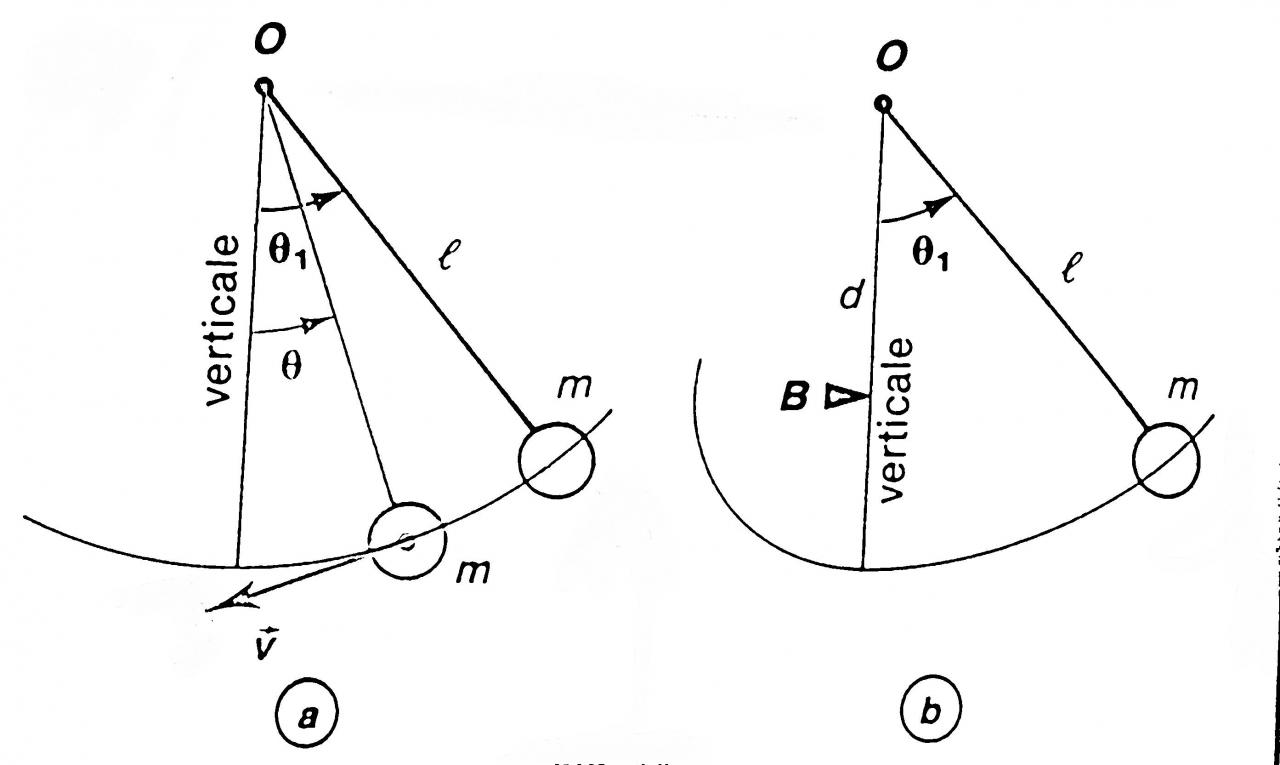
Énoncé. Une sphère de masse m = 100g de dimensions négligeables, est suspendue à un point fixe O par un fil sans masse et de longueur l=1m . Tous ses mouvements ont lieu dans le plan vertical .
a) On écarte le fil d'un angle teta1= 60 degres et on abandonne le pendule sans vitesse.
On choisit par convention l'énergie potentielle de la masse m égale à zéro lorsque celle-ci est dans le plan horizontal passant par O.
Calculer l'énergie mécanique de la sphère au départ du mouvement.
Que devient-elle si les oscillations s'effectuent sans frottement?
b) B3. Exprimer l'énergie mécanique E de la sphère en fonction de sa masse m, de sa vitesse v et de l'inclinaison e du pendule .
Calculer, en joules, l'énergie cinétique Ec}et l'énergie potentielle Ep de la sphère lorsqu'elle passe par sa position la plus basse.
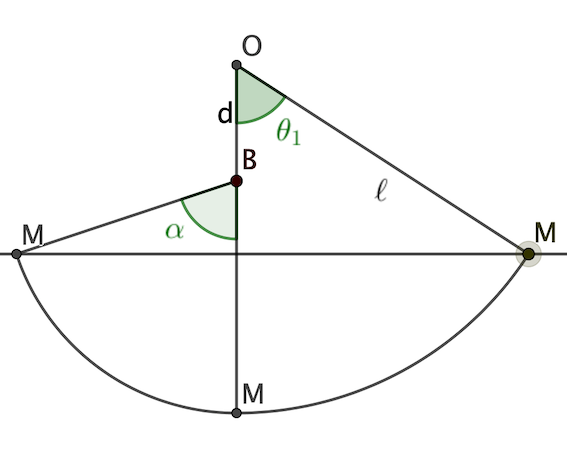
c) C1. On place maintenant, à la verticale de O mais au-dessous, une butée B à la distance OB = d de l'axe
Le pendule est encore lâché sans vitesse du point d'élongation teta1 = 60 degres
A quelle distance d1 de l'axe O faut-il placer la butée pour que la sphère remonte, après le choc, jusqu'à l'horizontale du point B?
On admet que le choc entre le fil et la butée s'effectue avec conservation de l'énergie cinétique.
Pour d < d1 calculer l'angle de remontée a de la masse m (avec la verticale).
J'avais commencé à répondre aux questions:
Em = Ec + Ep or Ec= 0
Em = - 1/2 mgl x cosinus téta1 = -0,245 J
Si il y a frottements deltaEm= Em - E mo=W(f)
Emo= Énergie mécanique a la position d'équilibre du système
b)
E = Ec + Ep
Ep = = mgh= -1/2mglCosteta
Ec= 1/2 mv^2
=) E= 1/2 mv^2 - 1/2mglCosteta
Calculons Ec et Ep
Ep =-mgħ =- 1 /2 mgl = - 1/2 (0,1)(9,8)(t) = - 0,49 J
Ec + Ep = - 0, 245 => 2Ec = - Ep - 0, 245
= 0,49-0,245= 0,245 J
c) Je bloque ici
-----